卷积神经网络：总结

Posted 2021-04-26 智能航空发动机

本文对于卷积神经网络（CNN）做一个总结，包括前向传播、反向传播以及代码实现。

01

原理

深度神经网络（DNN）是深度学习的基础，其本质上是多层神经网络。 DNN的训练过程可分为两个步骤，即前向传播与反向传播。 卷积神经网络（CNN）和循环神经网络（RNN）是DNN的两种变体，因此 CNN和RNN的训练过程与DNN类似，也是分为前向传播与反向传播两个步骤 。 但是，由于CNN和RNN用了特有的模块，在计算过程上会 与DNN 有所不同。

（一）前向传播

CNN的前向传播过程和DNN类似，但由于CNN用了其特有的卷积层和池化层，因此在计算过程上会与DNN有所不同。

首先，在进行前向传播之前，需要弄清楚各层输出的维度。

参考：https://blog.csdn.net/weixin_30298497/article/details/95756601

1）输入：一张image的大小是28*28，minibatch的大小是150，所以输入就是一个28*28*150的矩阵。

2）Wc1,bc1：第一层卷积的权重和偏置。一共8个filter（卷积核），每个核的大小为5*5。

3）activations1：通过第一层卷积得到的feature map，大小为（28-5+1）*（28-5+1）*8*150，其中8是第一层卷积filter的个数，150是输入的image的个数。

4）activationsPooled1：将第一层卷积后的feature map进行采样后的feature map，大小为(24/2)*(24/2)*8*150=12*12*8*150。

5）Wc2,bc2：第二层卷积的权重和偏置。一共10个filter，每个大小为5*5*8。

注意第二层的权重是三维的。对于每张图像，第一层卷积+池化后输出的feature map是12*12*8，而第二层的一个filter和这个feature map卷积后得到一张8*8的feature map，所以第二层的filter都是三维的。

6）activations2：通过第二层卷积得到的feature map，大小为（12-5+1）*（12-5+1）*10*150=8*8*10*150，其中10是第二层卷积filter的个数，150是输入的image的个数。

7）activationsPooled2：将卷积后的feature map进行采样后的feature map，大小为(8/2)*(8/2)*10*150=4*4*10*150。

8）activationsPooled2'：第二层卷积完了之后，要把一张image对应的所有feature map reshape成一列，那么这一列的长度就是4*4*10=160，所以reshape后得到一个160*150的大feature map

9）Wd,bd：softmax层的权重和偏执。

10）probs：对所有图像所属分类的预测结果，每一列对应一张图像，一共10行，第i行代表这张图像属于第i类的概率。

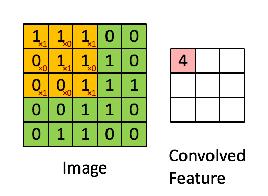
卷积操作就是将卷积核在图片上从左到右、从上到下依次滑动，在每次滑动后，将对应位置的元素相乘再相加。对于卷积核是三维的情况，计算过程类似，只不过是将三维卷积核在三维图片上依次滑动。卷积核中的参数和DNN中的权重一样，是需要通过网络学习得到的。

CNN的池化层很简单，分为最大池化和平均池化。池化层所起的作用是降维，即将大的图片转化为小的图片。池化层和卷积层类似，也是用一个类似“卷积核”的局部方框在图片上从左到右、从上到下依次滑动。换一个角度理解，其实池化层也相当于一种卷积核，只不过这种“池化卷积核”的参数比较特殊：如果是最大池化，则该卷积核的参数只在最大元素处为1，其余位置为0；如果是平均池化，则该卷积核的参数都为1/（k*k），其中k为“池化卷积核”的大小。

（二）反向传播

与深度神经网络（DNN）的反向传播过程类似，CNN的反向传播过程包括求解目标函数关于参数的导数以及更新参数这两个步骤。CNN主要由卷积层、池化层和全连接层组成。其中，只有卷积层和全连接层有参数，而池化层没有参数。因此，只需要更新卷积层和全连接层的参数。

由于前向传播的过程中是依次计算卷积层、池化层和全连接层的输出，那么在反向传播的过程中是将误差依次从全连接层传播到池化层，再到卷积层。

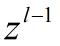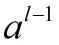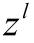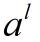对于卷积、池化和全连接层的误差反向传播过程是一样的：均需要先求出误差关于、、 、的导数，然后可以根据链式法则将误差逐层向前面的层递推。（先计算误差递推公式，再计算误差关于参数的导数）

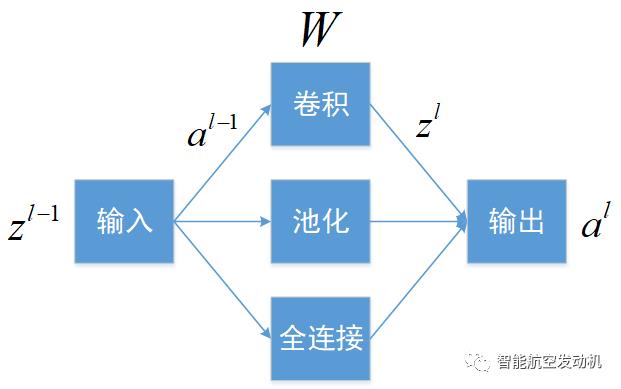
全连接层的反向传播过程与DNN一致，直接将后一层的误差导数乘以它之前的权重，即可得到前一层的误差导数。

若要计算误差E相对于池化层输入的导数，则需要先将池化层输出的误差矩阵还原成池化层输入的形状。若采用平均池化，则池化层输出的误差矩阵中的每个元素由池化方框中的所有元素均分；若采用最大池化，则池化层输出的误差矩阵中的每个元素只由池化方框中的最大元素负责。

卷积层的误差递推公式由下图可知。

有了三种类型层的误差递推公式，则可进一步求出误差关于参数的导数。值得注意的是，卷积层的误差递推公式需要旋转180度，而在计算误差关于参数的导数时，则不需要旋转。

02

代码

编码原则：先搭整体框架，再填充细节。

以一层卷积 + 一层池化 + 一层全连接层为例，给出前向传播和反向传播的代码实现。

（一）前向传播

% cnnConvolve代表卷积操作，需自己实现activations = cnnConvolve(filterDim, numFilters, mb_data, Wc, bc); 
% cnnPool代表池化操作，需自己实现activationsPooled = cnnPool(poolDim, activations);
% reshape代表将池化后的输出展开成一个列向量，是matlab自带函数activationsPooled = reshape(activationsPooled,[],numImages);
% 计算全连接层的输出，并采用softmax函数作为输出层h = exp(bsxfun(@plus,Wd * activationsPooled,bd));probs = bsxfun(@rdivide,h,sum(h,1));

cnnConvolve()：需要理解conv2()函数内部实现的细节

function convolvedFeatures = cnnConvolve(filterDim, numFilters, images, W, b) % cnnConvolve() Returns the convolution of the features  % % Parameters: % filterDim - filter dimension % numFilters - number of filters % images - large images to convolve with, matrix in the form % images(r, c, image number) % W, b - W is of shape (filterDim,filterDim,numFilters) % b is of shape (numFilters,1) % % Returns: % convolvedFeatures - matrix of convolved features in the form % convolvedFeatures(imageRow, imageCol, numFilters, imageNum)
 imageDim = size(images,1); numImages = size(images,3); convDim = imageDim - filterDim + 1;
 % Instructions: % Convolve every filter with every image here to produce the  % (imageDim - filterDim + 1) x (imageDim - filterDim + 1) x numFeatures x numImages % matrix convolvedFeatures, such that  % convolvedFeatures(imageRow, imageCol, numFilters, imageNum) is the % value of the convolved (numFilters)_th feature for the (imageNum)_th image over % the region (imageRow, imageCol) to (imageRow + filterDim - 1, imageCol + filterDim - 1)
 convolvedFeatures = zeros(convDim, convDim, numFilters, numImages); for imageNum = 1:numImages for filterNum = 1:numFilters  % Obtain the filter filter = squeeze(W(:,:,filterNum)); % Flip the feature matrix because of the definition of convolution, as explained later % 因为在conv2()函数内部会自动逆时针旋转了180度，因此这里也需要逆时针旋转180度保持不变 filter = rot90(squeeze(filter),2);
 % Obtain the image im = squeeze(images(:, :, imageNum));
 % Convolve "filter" with "im", adding the result to convolvedImage % be sure to do a 'valid' convolution convolvedImage = conv2(im,filter,'valid');  % Add the bias unit convolvedImage = bsxfun(@plus,convolvedImage,b(filterNum));  % Then, apply the sigmoid function to get the hidden activation convolvedImage = 1 ./ (1+exp(-convolvedImage));
 convolvedFeatures(:, :, filterNum, imageNum) = convolvedImage; end endend

cnnPool()：池化层也相当于一种卷积核，只不过这种“池化卷积核”的参数比较特殊：如果是最大池化，则该卷积核的参数只在最大元素处为1，其余位置为0；如果是平均池化，则该卷积核的参数都为1/（k*k），其中k为“池化卷积核”的大小。因此，依然可以采用conv2()或convn()实现池化操作。

function pooledFeatures = cnnPool(poolDim, convolvedFeatures) % cnnPool() Pools the given convolved features % % Parameters: % poolDim - dimension of pooling region % convolvedFeatures - convolved features to pool (as given by cnnConvolve) % convolvedFeatures(imageRow, imageCol, featureNum, imageNum) % % Returns: % pooledFeatures - matrix of pooled features in the form % pooledFeatures(poolRow, poolCol, featureNum, imageNum) %   convolvedDim = size(convolvedFeatures, 1); numFilters = size(convolvedFeatures, 3); numImages = size(convolvedFeatures, 4);  pooledFeatures = zeros(convolvedDim / poolDim, ... convolvedDim / poolDim, numFilters, numImages);
 % Instructions: % Now pool the convolved features in regions of poolDim x poolDim, % to obtain the  % (convolvedDim/poolDim) x (convolvedDim/poolDim) x numFeatures x numImages  % matrix pooledFeatures, such that % pooledFeatures(poolRow, poolCol, featureNum, imageNum) is the  % value of the featureNum feature for the imageNum image pooled over the % corresponding (poolRow, poolCol) pooling region. 
 % Use mean pooling here. for imageNum = 1:numImages for featureNum = 1:numFilters featuremap = squeeze(convolvedFeatures(:,:,featureNum,imageNum)); pooledFeaturemap = conv2(featuremap,ones(poolDim)/(poolDim^2),'valid'); pooledFeatures(:,:,featureNum,imageNum) = pooledFeaturemap(1:poolDim:end,1:poolDim:end); end endend

（二）反向传播

定义并计算目标函数：梯度下降要优化的目标函数，主要分为两部分：一部分是由于分类器输出结果和真实结果的差异引起的误差，另一部分是对权重w的正则约束。

logp = log(probs);index = sub2ind(size(logp),mb_labels',1:size(probs,2));ceCost = -sum(logp(index));wCost = lambda/2 * (sum(Wd(:).^2)+sum(Wc(:).^2));cost = ceCost/numImages + wCost;

交叉熵损失函数关于softmax层输入的导数为 直接用预测结果减去真实结果。 本文采用分类问题常用的交叉熵损失函数。

output = zeros(size(probs));output(index) = 1;DeltaSoftmax = probs - output;

全连接层的误差反向传播是将 DeltaSoftmax乘以各层的权重以及点乘激活函数的导数。

Wd_grad = (1./numImages) .* DeltaSoftmax*activationsPooled'+lambda*Wd;bd_grad = (1./numImages) .* sum(DeltaSoftmax,2);

在求出误差关于第一个全连接层的导数后，需要将该结果还原成最后一个池化层输出的形状。如果采用的是平均池化，则误差在池化区域内的所有元素上均分；如果采用的是最大池化，则误差只由最大元素负责。

DeltaPool = reshape(Wd' * DeltaSoftmax,outputDim,outputDim,numFilters,numImages);DeltaUnpool = zeros(convDim,convDim,numFilters,numImages);
for imNum = 1:numImages for FilterNum = 1:numFilters unpool = DeltaPool(:,:,FilterNum,imNum); DeltaUnpool(:,:,FilterNum,imNum) = kron(unpool,ones(poolDim))./(poolDim ^ 2); endend

卷积层的反向传播较为复杂，但是具体的推导细节已经在《卷积神经网络（三）：反向传播过程》中解释清楚。

% 在求出误差关于池化层输入的导数后，再点乘激活函数的导数。DeltaConv = DeltaUnpool .* activations .* (1 - activations);
% 卷积层偏置的代码bc_grad = zeros(size(bc));for filterNum = 1:numFilters error = DeltaConv(:,:,filterNum,:); bc_grad(filterNum) = (1./numImages) .* sum(error(:));end
% 卷积层权重的代码Wc_grad = zeros(filterDim,filterDim,numFilters);% 旋转所有DealtaConv：下面的conv2在函数内部会自动旋转180度，% 所以在这里旋转是为了抵消conv2旋转的影响。for filterNum = 1:numFilters for imNum = 1:numImages error = DeltaConv(:,:,filterNum,imNum); DeltaConv(:,:,filterNum,imNum) = rot90(error,2); endend
for filterNum = 1:numFilters for imNum = 1:numImages Wc_grad(:,:,filterNum) = Wc_grad(:,:,filterNum) + conv2(images(:,:,imNum),DeltaConv(:,:,filterNum,imNum),'valid'); endendWc_grad = (1./numImages) .* Wc_grad + lambda*Wc;

整体代码参考：https://github.com/sunshineatnoon/Single-Layer-CNN-on-MNIST