基于ESMD-BP神经网络组合模型的中长期径流预报 Posted 2021-04-26 山坡水文土壤前沿瞭望
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于ESMD-BP神经网络组合模型的中长期径流预报相关的知识,希望对你有一定的参考价值。
题目:基于ESMD-BP神经网络组合模型的中长期径流预报
期刊/链接:JOURNAL OF BASICSCIENCE AND ENGINEERING/doi:10. 16058 / j. issn. 1005- 0930. 2020. 04. 006
径流预报的精度直接关系到流域水资源优化配置与综合利用的效益最大化,针对径流序列非线性、非平稳、直接预测精度低的特点,首次利用具有自适应性特点的极点对称模态分解(Extreme-point Symmetric Mode Decomposition,ESMD)方法对径流序列平稳化处理,结合可逼近任何非线性映射的误差反向传播网络(Back Propagation Neural Network,BP神经网络),建立ESMD-BP神经网络组合预报模型,并将其应用于黄河上游龙羊峡水库入库站唐乃亥站月径流和旬径流预报。
首先,利用ESMD方法将径流序列中不同尺度的分量和趋势分量逐级提取出来,甄别了大尺度循环和非线性趋势;进而,分析径流周期和趋势变化规律;然后,利用BP神经网络将非平稳径流序列的直接预测转化为平稳的模态分量和趋势余项的预测,加和重构得到最终预测结果。并与单一BP神经网络、经验模态分解 (Empirical Mode Decomposition,EMD)与BP神经网络组合模型作对比,结果表明:ESMD-BP神经网络组合模型的预报误差最小、预报精度最高。组合模型为“分解→预测→重构”模式,结合了EMD数据自适应分析和BP神经网络非线性映射的优点,提高了径流预报的准确率,为水文预报精度的提高开辟了新思路。
鉴于ESMD方法继承了EMD方法的所有优点,同时解决了EMD方法分解出的趋势函数太粗略、筛选次数难以确定和“模态混叠”的问题,利用ESMD方法具有基于信号局部变化、自适应、无基的特点,能够逐级分解出具有不同频率的模态分量和趋势余项,将非平稳的径流序列趋于平稳化,甄别了大尺度循环和非线性趋势,与BP神经网络建立非线性映射的使其具备自学习和自适应的反馈逼近能力,构建出ESMD-BP神经网络组合预报模型,对径流进行中长期预报。
首先,利用ESMD的内部极点对称插值处理径流序列,构造插值曲线,降低了由插值带来的不确定性。其次,基于ESMD具有信号局部变化,不需要基函数,以自适应的方式将径流序列逐级分解为高频到低频的模态分量和趋势余项,摆脱了数学理论限制。同时将非平稳径流列趋于平稳化,识别了径流序列的周期和趋势成分。进而,采用FFT周期图计算各模态分量的周期,得到径流序列的不同周期变化规律;分析不同尺度下径流振幅波动的情况,得到径流序列不同时间尺度的变化过程;通过ESMD方法提供的数据自适应拟合手段,使趋势余项为最佳自适应全局均线时,分析趋势余项的变化,得到径流序列的整体变化过程;掌握不同时间尺度的径流序列多年变化规律,为中长期径流预报奠定基础。然后,将分解得到的各个模态分量和趋势余项分别作为BP神经网络的输入数据,利用BP神经网络自学习、自适应、非线性逼近的特点,计算出预见期各模态分量和趋势余项的预测值。加和重构各序列预测结果,得到ESMD-BP组合预报模型的最终预测结果。最后,采用预报合格率、预报精度等级、平均相对误差、均方根误差和确定性系数评价模型的性能,并与单一BP神经网络模型和EMD-BP神经网络组合模型的预测结果进行对比分析。
ESMD-BP神经网络组合预报模型,采用ESMD方法分解径流序列,再利用BP神经网络分别预测分解得到的模态分量和趋势余项,加和重构得到最终预测结果。这种组合预报模型为“分解→预测→重构”模式,将径流序列的直接预测转化为对一系列模态分量和趋势余项的预测,充分利用了ESMD方法的非平稳径流序列平稳化技术和BP神经网络非线性逼近的特点,正适合于非线性、非平稳径流序列的径流预报。
本文选取黄河上游龙羊峡水库入库径流站唐乃亥水文站1956~2017年的实测年径流、月径流和旬径流数据资料,首先利用ESMD方法在数据分析方面的优势,分析唐乃亥站多年径流量的变化规律,为径流预报提供有用的信息;然后采用ESMD-BP神经网络组合模型,对唐乃亥站月径流和旬径流序列进行预报,从而进行龙羊峡水库的入库径流预报。
图1唐乃亥水文站地理位置
3.1 ESMD-BP组合模型的径流预报
采用ESMD方法将唐乃亥站月径流和旬径流序列中不同频率的波动和趋势逐级分解开来,生成一系列包含了原始信号中不同时间尺度变化特征的模态分量和一个趋势余项,将非平稳序列转化为了平稳序列。再利用BP神经网络非线性逼近的特点,将对径流序列的直接预测转化为对各模态分量和趋势余项的预测。接下来,将建立的ESMD-BP神经网络组合模型应用到唐乃亥站月径流和旬径流序列的预报中。
3.1.1月径流预报
取唐乃亥水文站1956~2017年共744个月的实测月径流时间序列,以1956.01~2010.12(共660个月)的数据为训练样本,2011.01~2017.12(共84个月)的数据为验证样本。利用BP神经网络的自适应、自学习和非线性逼近的特点分别对分解得到的模态分量和趋势余项进行预测。叠加各序列的预测结果,得到组合模型对原始序列的最终预测结果。为了比较ESMD-BP神经网络组合模型的预报效果,本文采用单一BP神经网络和EMD-BP神经网络组合模与其对比。如图2为3种模型预测结果与实测数据的对比图。
图2 1956~2017年唐乃亥站月径流量预报结果
从图2中可以看出:单一BP神经网络和EMD-BP组合模型的预测值与实测数据误差较大,ESMD-BP组合模型的预测结果更接近实际径流,充分体现了ESMD-BP组合模型在中长期径流预报中的优越性。从图中可以看到月径流序列存在12月的周期规律,呈现出非线性的上升∽下降循环出现的趋势变化,表明ESMD方法对月径流序列分析的准确性,可为径流预报提供有参考价值的信息。为了定量评定模型的预测效果,采用QR预报精度等级、MAPE、RMSE和DC评价模型的性能,结果见表1。
表1唐乃亥站各模型月径流序列预报结果
从表1中可以看到:单一BP神经网络的预报精度等级为丙等,两种组合模型的预报精度等级为乙等,表明组合模型可以提高径流预报的精度。单一BP神经网络和EMD-BP组合模型的预报合格率分别为54.76%和61.90%,而ESMD-BP组合模型的预报合格率为70.24%,比单一BP神经网络和EMD-BP组合模型分别提高了28.27%和13.47%,ESMD-BP组合模型有效地提高了预报合格率。从单一BP神经网络、EMD-BP组合模型到ESMD-BP组合模型的平均相对误差、均方根误差逐渐减小,确定性系数逐渐提高。与单一BP神经网络模型相比,ESMD-BP组合模型的平均相对误差减少了33.95%,均方根误差降低了47.09%,确定性系数提高了48.90%;与EMD-BP组合模型相比,平均相对误差减少了22.48%,均方根误差降低了5.14%,确定性系数提高了19.81%;表明ESMD-BP组合模型减小了径流预报误差,提高了径流预报的准确率。
径流是非平稳序列,采用BP神经网络对径流序列直接预测效果不太理想;EMD方法虽然可以将非平稳序列平稳化处理,但在对径流序列分解中,可能存在模态混叠问题,导致径流序列分解得到的模态分量丧失具体物理意义,对径流预测的准确率造成影响;ESMD-BP神经网络组合模型,既可以将非平稳径流序列的直接预测转换为平稳的不同频率模态分量的预测,也克服了EMD模态混叠的问题,有效地提高了径流预报精度。
3.1.2旬径流预报
为了进一步体现ESMD-BP神经网络组合模型在中长期径流预报中的优势,采用同样的方法对唐乃亥站1956~2017年的旬径流时间序列进行预报。以1956.01~2010.12(共1980旬)的数据作为训练样本,2011.01~2017.12(共252旬)的数据作为验证样本。为了更加直观地观察组合模型的预测情况,同样作出单一BP神经网络模型、EMD-BP组合模型和ESMD-BP组合模型的预测结果与实测径流数据的对比图,见图3。
图3 1956~2017年唐乃亥站旬径流预报结果
从图3中可以看到:从模型预测结果和实测数据拟合效果来看:ESMD-BP组合模型>EMD-BP组合模型>单一BP神经网络,从图中可以看到旬径流序列主要存在36旬的周期规律,呈现出“上升∽下降∽上升”交替出现的趋势变化,进一步验证了ESMD方法对径流序列分析的可行性,可为径流预报提供依据。同样,采用5个性能评价指标来度量模型预报的精度,见表2。
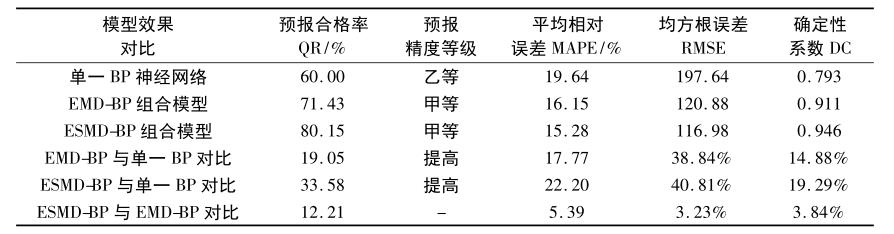
表2 唐乃亥站各模型旬径流序列预报结果
从表2中可以看到:单一BP神经网络的预报合格率为60%,预报精度等级为乙等;EMD-BP组合模型的预报合格率为71.43%,ESMD-BP组合模型的预报合格率为80.15%,两种组合模型预报精度等级均为甲等;与单一BP神经网络模型相比,两种组合模型的预报合格率分别提高了19.05%和33.58%,预报精度等级从乙等提高到甲等。同时EMD-BP组合模性和EMSD-BP组合模型比单一BP神经网络模型预测结果的平均相对误差分别减少了38.24%和46.48%,均方根误差分别降低了38.84%和40.81%,确定系数分别提高了14.88%和19.29%。表明采用这种“分解→预测→重构”模式的组合模型,将非平稳径流序列的直接预测转化为平稳的高频分量、低频分量和趋势余项的预测,可以提高径流预报的精度。对比两种组合模型,ESMD-BP组合模型比EMD-BP组合模型预测结果的平均相对误差降低了5.39%,均方根误差减少了3.23%,确定性系数提高了3.84%,ESMD-BP组合模型解决了EMD-BP组合模型“模态混叠”影响径流预测结果的问题,提高了径流预报的准确率,体现了该模型在中长期径流预报中的优越性。
3.1.3不同时间尺度径流预报对比分析
将ESMD-BP神经网络组合模型分别对唐乃亥站月径流和旬径流序列预测的结果进行对比分析,见表.。表.中采用预报合格率、预报精度等级、平均相对误差、均方根误差和确定性系数,对月径流和旬径流预测结果的精度进行评价,从表.中可以看到:与月尺度相比,旬尺度的预报合格率相对提高了14.11%,预报精度等级从乙等提高到甲等。旬尺度的预报精度大幅度提高,表明时间尺度变小,径流预报精度提高。同时,旬尺度比月尺度预测结果的平均相对误差相对降低了30.86%;均方根误差相对降低了28.20%;确定性系数相对提高了7.13%。进一步说明了旬尺度预测的误差变小,预测结果更接近实测数据。在径流预报中,时间尺度的选择可以影响预报的精度,与文献中的结果基本一致。在提出新方法的基础上,从时间尺度的选择方面考虑预报精度,为预报精度的提高又提供了一种新思路,可以更准确地为水库调度及水资源运行管理提供依据。
表3唐乃亥站不同时间尺度径流预报结果对比
针对径流序列非线性非平稳的特点,利用ESMD方法不需要基函数,可以自适应地将非平稳的径流序列分解为不同时间尺度的分量,使径流序列趋于平稳化,再利用BP神经网络非线性逼近的特点,建立ESMD-BP神经网络组合模型,对分解得到的模态分量和趋势余项分别进行预测,加和重构,得到最终预测结果。并采用单一BP神经网络和EMD-BP组合模型作对比,得到如下结论:
(1)ESMD-BP神经网络组合模型结合了ESMD方法的非平稳径流序列平稳化技术和BP神经网络的非线性映射逼近优势,具有自学习和自适应性的优点;
(2)将ESMD-BP组合模型应用到唐乃亥水文站月径流和旬径流预报中,采用单一BP神经网络和EMD-BP组合模型作对比分析。结果表明:ESMD-BP组合模型减少了非平稳性对误差的影响,克服了EMD模态混叠的问题,提高了径流预报的准确率;
(3)ESMD-BP组合模型对旬尺度预报精度高于月尺度的预报精度,表明时间尺度的选择影响径流预报精度,时间尺度变小,可以提高预报精度;
(4)ESMD和BP神经网络结合的模型在唐乃亥站的径流预报中取得了良好效果,可将这两种方法的组合模型应用到其他水文站的中长期径流预报中。
【1】ZhangWeiguo,ZhongPing’an,ZhangYulan.Aseasonalsupportvectormachinemid-longtermrunoffforecastmodel[J].HydroelectricPower,2014,40(4):16-21
【2】LiHongyan,LiuHanbing,FanXimin。Peak value recognition the oryofartificialneural network and its application to flood forecasting[J].JournalofHydraulicEngineering,2002,33(6):15-20
以上是关于基于ESMD-BP神经网络组合模型的中长期径流预报的主要内容,如果未能解决你的问题,请参考以下文章
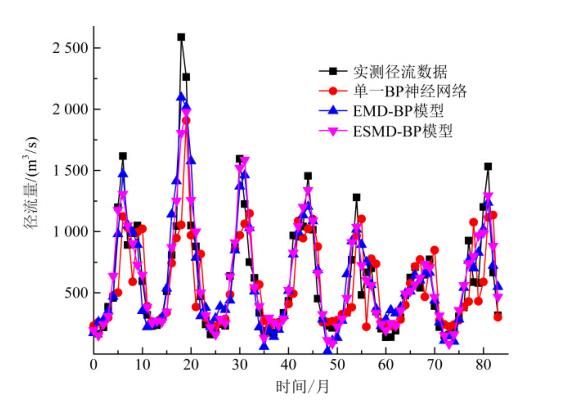 图2 1956~2017年唐乃亥站月径流量预报结果
图2 1956~2017年唐乃亥站月径流量预报结果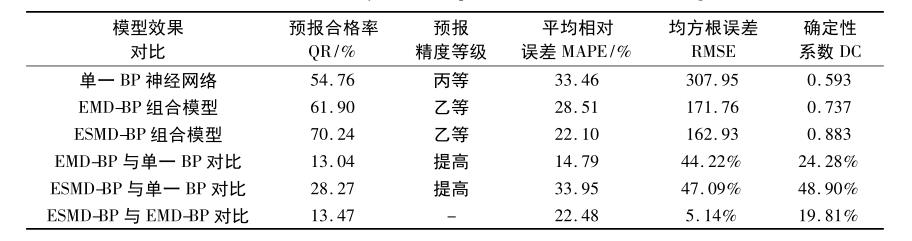
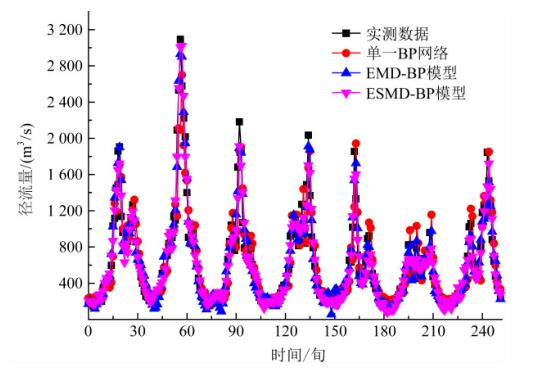 图3 1956~2017年唐乃亥站旬径流预报结果
图3 1956~2017年唐乃亥站旬径流预报结果