神经网络简介二
Posted 郭老师统计小课堂
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了神经网络简介二相关的知识,希望对你有一定的参考价值。
-
本文部分图片来源于网络,如有侵权,请告知,我们将立即调整! -
本文主要讲解反馈全连接神经网络。
2.3 反向传播的算法表达
神经网络的结构为:
其中,共有隐藏层 层,每一层分别记为 ,每一层神经元的个数为 ,隐藏层的是激活函数为 ,输出层的激活函数为 ,为方便起见,将输出层记为 层。每一层的权重为:
此处也仅考虑一个样本的情况, ,因变量为 。神经网络的前向传播为:
令 为样本 的损失,定义误差为:
关于误差 ,有如下递推公式:
可以计算梯度:
其中定义
。
算法为:
(1) 正向计算:
(2) 反向计算:
(3) 更新参数:
3. 神经网络一些重要的细节
本节将介绍神经网络一些重要的细节,主要涉及梯度消失、随机梯度下降、过拟合和欠拟合、损失函数等内容。
3.1 损失函数的选取
此部分内容在之前的推送中已经涉及到,主要思路是由极大似然出发,推导出极大似然估计下的损失函数等价于交叉熵,对于不同的响应变量类别,采用不同的交叉熵形式即可,总结下来是:
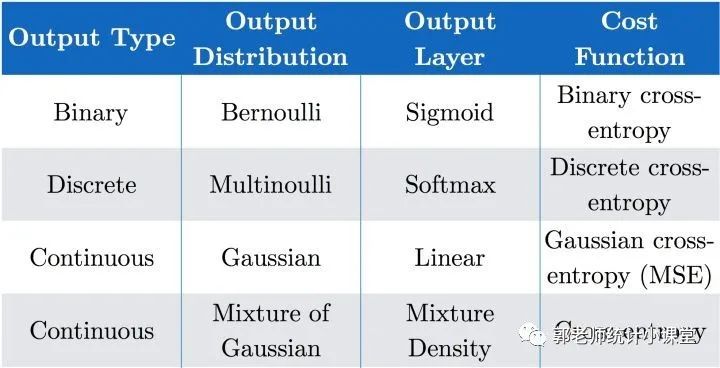
3.2 随机梯度下降
首先看,我们原始的全批量梯度下降法有什么缺点,简单来说,最大的缺点就是计算量大,更新一次参数需要计算每个样本点的梯度,耗费时间。对于全批量的梯度下降(Bach Gradient Descent,BGD)为:
对应的随机梯度下降(Stochastic Gradient Descent, SGD)为:
二者的折中方案小批量梯度下降为(Minibatch Gradient Descent, MBGD):
可以看到随机梯度下降仅计算了一个点的梯度,用该点的梯度来更新一次参数,而批量梯度下降是采用了batch_size个点的梯度平均值来更新参数,这样的作法为什么是有效的呢?
对于一个理想的的损失函数,应当是如下的形式:
其中,随机变量 为我们此处的自变量, 表示随机变量在 时的取值。梯度的理想形式为:
但是在实践中,我们往往是不知道 的密度函数 ,因此上述的期望无法计算,只能由样本估计。即:
该估计是上述期望的无偏估计。事实上:
-
M=1 时,对应着SGD; -
M=N时,对应着BGD; -
1<M<N时,对应着MBGD;
因此三种方法计算的梯度不过就是总体梯度的一个估计而已,并且它们都是无偏的,只不过M=N时估计更加有效,也就是所谓的估计得“更准”。然而在实际过程中,我们可能并不一定要这个估计量很准,在训练的初始阶段,我们只用知道参数大概的更新方向,然后快速地沿着这个方向更新,在参数值逼近极值点时,再采取一定的策略使得参数缓慢更新(例如可变的学习率等),随机梯度下降正好满足这个要求!在实践中SGD和MBGD运用的非常广泛,效果也不错。
接着3.3-3.4会讲述欠拟合的处理方法,3.5会讲述过拟合处理方法。
3.3 梯度消失问题
梯度消失是一种常见的欠拟合的现象,先来看看什么是梯度消失。前述神经网络的输出为:
由前面所提到的梯度下降过程倒数第 层参数的变化量为:
我们前面所述神经网络激活函数只介绍了sigmoid函数:
其函数图像为:
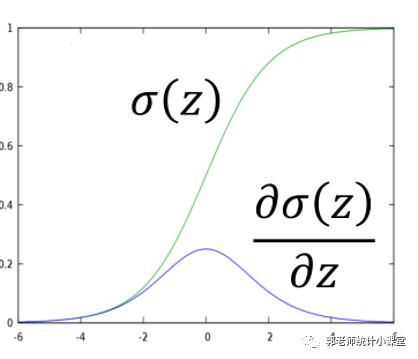
这样会造成原理输出层的参数 值非常小,参数几乎更新不了,当靠近输出层的参数已经更新好之后,远离输出层的参数却几乎没有变化,这样就造成了模型参数无法达到最优,从而欠拟合。
怎样解决呢?很直观的想法就是找一个导数值不小于1的激活函数形式就可以避免梯度消失,但是导数值也不能大于1,这样同样会造成梯度爆炸现象。那么选择好像就只剩下了线性函数了 。但是我们当初引入激活函数的目的就是为网络引入非线性部分,现在绕了一圈却又只能选择一个线性的函数?于是,ReLU激活函数就出现了:
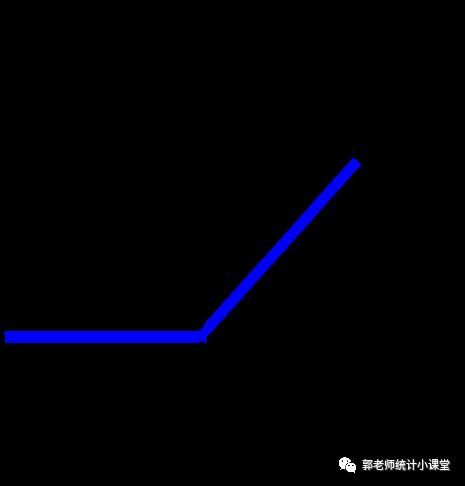
该函数首先是非线性的,其次导数值为1或者0(当z=0时的导数取单边的导数即可),并且这个函数的导数非常容易计算,直接判断z的正负即可。在此基础上还发展出了
以上是关于神经网络简介二的主要内容,如果未能解决你的问题,请参考以下文章