支持向量机
Posted 不成为ML大神不改名
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了支持向量机相关的知识，希望对你有一定的参考价值。
一个数学所的童鞋曾说过：我以前学的数学感觉都没有什么用，直到我学了机器学习，我才发现我可能学了一个假数学。
一 简介
支持向量机基本算是最好的监督学习算法了。最开始接触SVM是在大四上学期做算法学习的时候用到了这个，后来还做了一个关于SVM的报告文档。这次重新学SVM，更加清晰的从数学角度了解关于SVM算法的本质东西。这份笔记从感知机开始入手，到线性可分支持向量机再到线性支持向量机再到非线性支持向量机，一步步过渡过来，慢慢学习，更加自然。
二 感知机
感知机模型如下：
f(x)= sign(w*x+b)
其中，x为输入向量，sign为符号函数，括号里面大于等于0，则其值为1，括号里面小于0，则其值为-1。w为权值向量，b为偏置。求感知机模型即求模型参数w和b。感知机预测，即通过学习得到的感知机模型，对于新的输入实例给出其对应的输出类别1或者-1。
感知机学习策略是将训练数据集中正负实例通过找到的分类超平面完全划分来，即需要确定参数w和b，并且需要定义一个损失函数，并满足损失函数最小化的参数。损失函数可以定义为实例点到分类超平面的最小几何间隔(区别于函数间隔)，定义此几何间隔为：
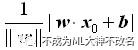
其中||w||是w的L2范数。
对于误分类点来说，当-yi (wxi + b)>0时，yi=-1，当-yi(wxi + b)<0时，yi=+1。所以对误分类点（xi, yi）满足：
-yi (wxi +b) > 0
所以误分类点（xi, yi）到分类超平面S的距离是：
而具体的感知机算法是这样的：首先任取一个超平面，即确定w0,b0,然后通过对损失函数求导计算最小值对w和b不断修正，重复计算损失函数，直至损失函数为0.上述这一过程教材上被称为随机梯度下降法。
感知机学习算法的原始形式：
这种算法的基本思想是：当一个实例点被误分类，即位于分类超平面错误的一侧时，则调整w和b，使分类超平面向该误分类点的一侧移动，以减少该误分类点与超平面的距离，直到超平面越过该误分类点使其被正确分类为止。
由算法可知，不同的初始值的选择最后得到的超平面的解可能不止一个，所以为了得到唯一的超平面的解，我们需要增加一些约束条件，这就是后面要讲的支持向量机的想法。并且当面对线性不可分的数据集时，此算法不会收敛。
下面介绍感知机学习算法的对偶形式，这个也很简单，就是抓住每次迭代过程中w和b的变化，将其表示为实例xi和标记yi的线性组合形式，通过求解其系数而求得w和b。对误分类点（xi, yi）通过
由此，类比于感知学习机的原始算法，我们总结出感知学习机的对偶形式的算法：
与原始形式一样，处理线性可分数据的时候，感知机学习算法的对偶形式迭代过程也是收敛的，存在多个解。
三 支持向量机
支持向量机是一种二类分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使他区别于感知机，还包括核技巧，使其可以推广到非线性分类器。总的来说，支持向量机的学习策略是使间隔最大化，从而使问题转化为凸二次规划问题，可以使用对偶算法，应用拉格朗日对偶性通过求解对偶问题得到原始问题的最优解。所以首先先学习一下拉格朗日对偶性的知识。
1 拉格朗日乘子法
拉格朗日乘子法适用于求解组合优化问题，例如下面的等式约束的极值问题的求解。
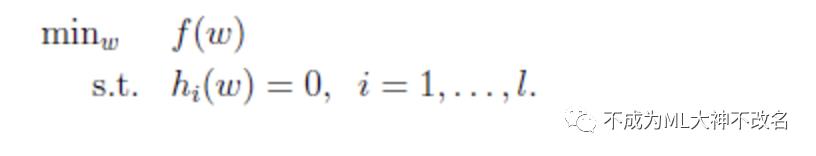
目标函数是f(w)，下面是等式约束。通常解法是引入拉格朗日算子，这里使用来表示算子，得到拉格朗日公式为
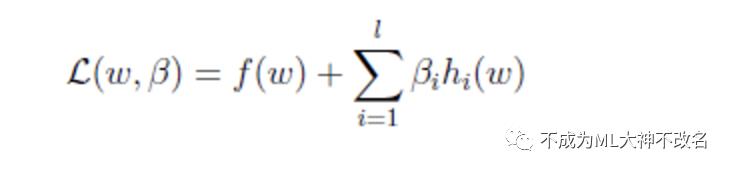
其中，l是约束条件的个数。
然后分别对w和求偏导，使得偏导数等于0，然后解出w和t。至于为什么引入拉格朗日算子可以求出极值，原因是f(w)的dw变化方向受其他不等式的约束，dw的变化方向与f(w)的梯度垂直时才能获得极值，而且在极值处，f(w)的梯度与其他等式梯度的线性组合平行，因此他们之间存在线性关系。（参考《最优化与KKT条件》）。
接下来探讨一下不等式约束的极值问题求解。
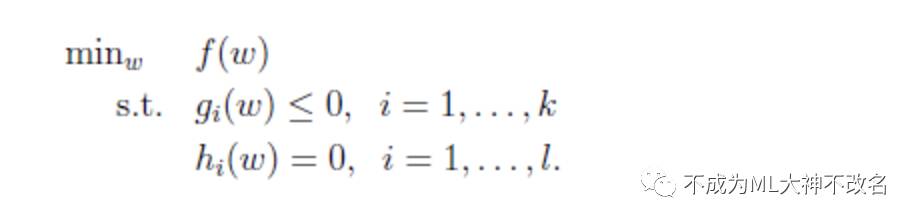
其拉格朗日公式为：
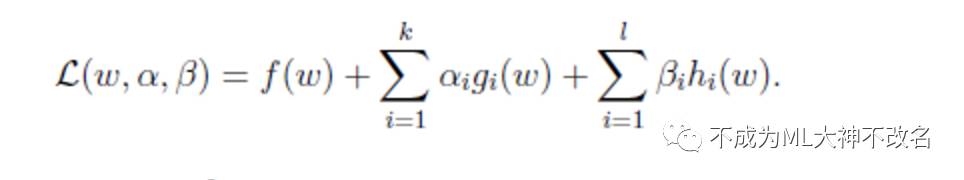
这里的a和b都是拉格朗日算子。如果按这个公式求解，会出现问题，因为我们求解的是最小值，而这里的已经不是0了，我们可以将a调整成很大的正值，来使最后的函数结果是负无穷。因此我们需要排除这种情况，我们定义下面的函数：
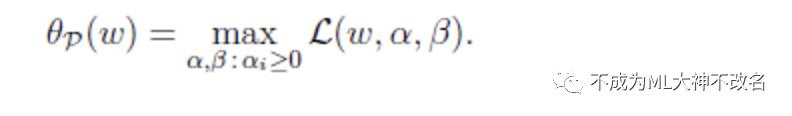
这里的P代表原始问题。假设g(w)>0或者h(w)>0，那么我们总是可以调整a和b来使得有
最大值为正无穷。而只有g和h满足约束时，为f(w)。这个函数的精妙之处在于a>0，而且求极大值。
(此处数学推导相当无聊。。。并且需要看非线性规划，最优化与KKT条件等书，所以此处直接截图，源于李航的《统计学习方法》附录3)
这部分内容思路比较凌乱，还需要先研究下《非线性规划》中的约束极值问题，再回头看看。KKT的总体思想是将极值会在可行域边界上取得，也就是不等式为0或等式约束里取得，而最优下降方向一般是这些等式的线性组合，其中每个元素要么是不等式为0的约束，要么是等式约束。对于在可行域边界内的点，对最优解不起作用，因此前面的系数为0。
重新回到SVM的问题上来。
定义几何间隔。
如图：
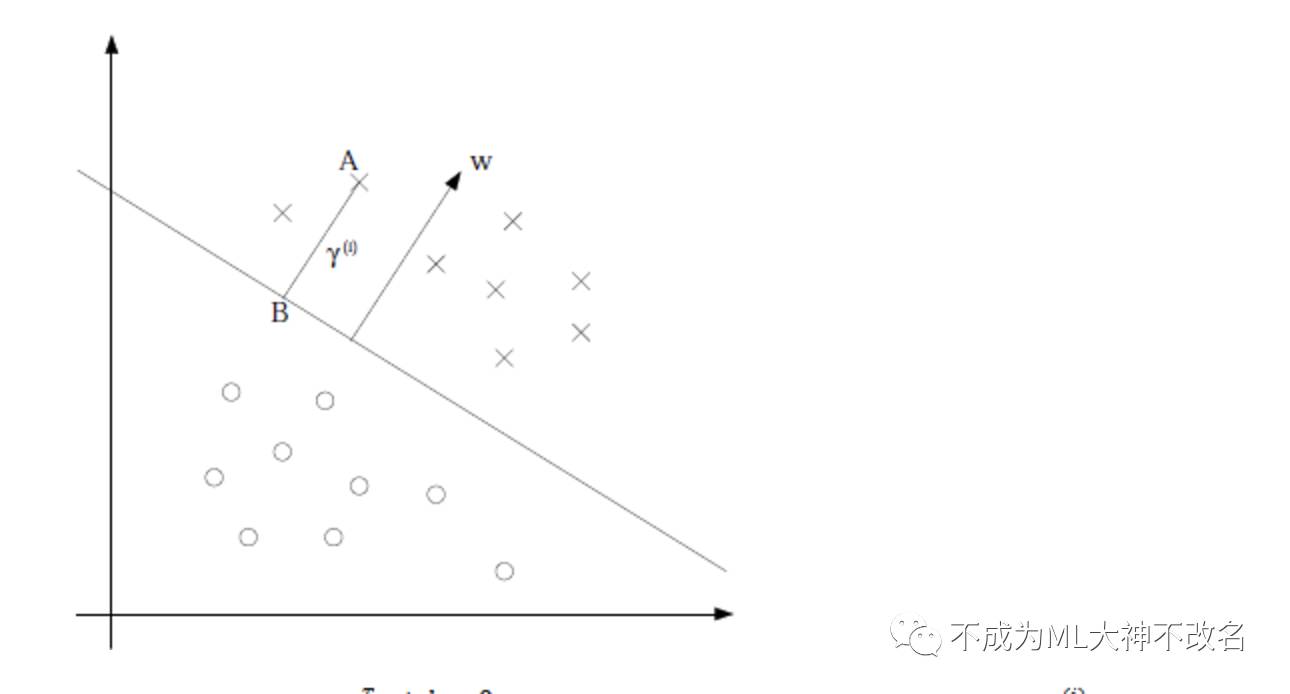
假设我们有了B点所在的
分割面。任何其他一点，比如A到该面的距离以
表示，假设B就是A在分割面上的投影。我们知道向量BA的方向是
（分割面的梯度），单位向量是
。A点是
，所以B点是x=
（利用初中的几何知识），带入得，
进一步得到
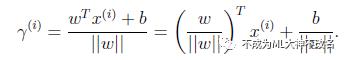
实际上就是点到平面距离。
换种更加优雅的写法：
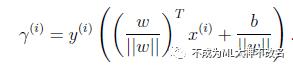
当
时，不就是函数间隔吗？是的，前面提到的函数间隔归一化结果就是几何间隔。他们为什么会一样呢？因为函数间隔是我们定义的，在定义的时候就有几何间隔的色彩。同样，同时扩大w和b，w扩大几倍，
就扩大几倍，结果无影响。同样定义全局的几何间隔
接下来定义最大间隔。
回想前面我们提到我们的目标是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。形象的说，我们将上面的图看作是一张纸，我们要找一条折线，按照这条折线折叠后，离折线最近的点的间距比其他折线都要大。形式化表示为：
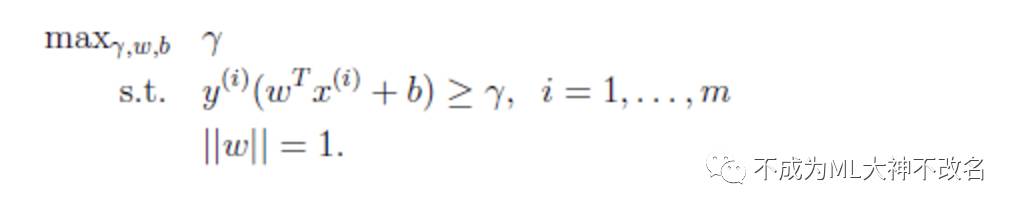
同样可转化为：
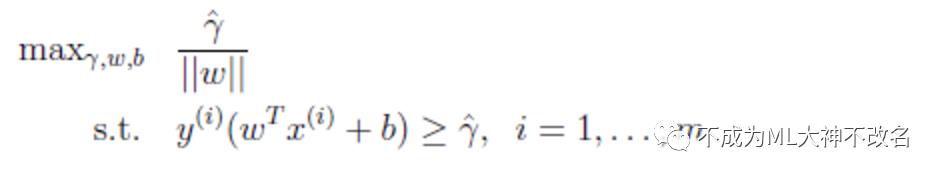
求解其最大值，可以转化为求1/2*||w||^2最小值。
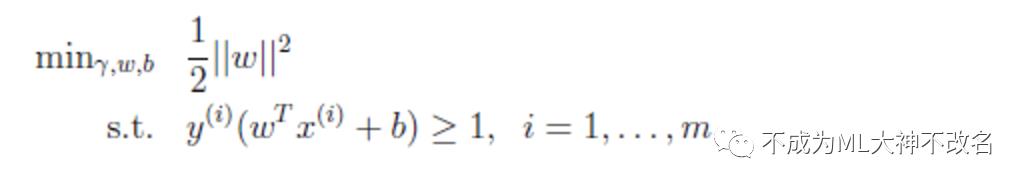
对该问题：
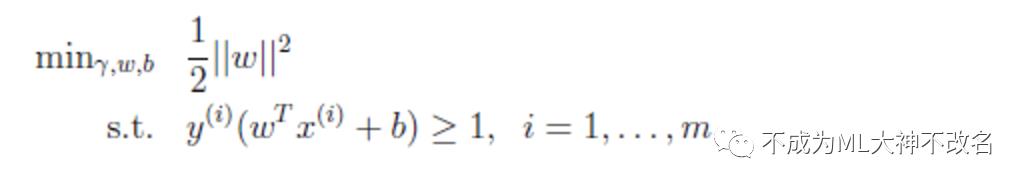
可以将约束条件改写为：
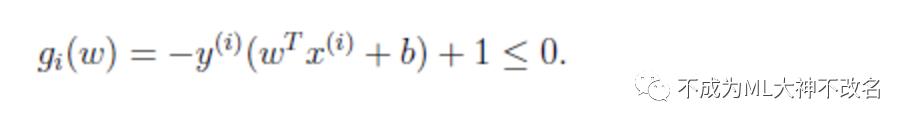
从KKT条件得知只有函数间隔是1（离超平面最近的点）的线性约束式前面的系数a=0，也就是说这些约束式g(w)=0，对于其他的不在线上的点(g(w)<0)，极值不会在他们所在的范围内取得，因此前面的系数a=0.注意每一个约束式实际就是一个训练样本.
对这样一个问题，通过一大串的数学证明，大概就是使用KKT条件，对偶问题，求偏导，求拉格朗日函数，将一个极小极大问题转化为极大极小问题。
总而言之，这一大串数学证明和计算，只为了得到下面的算法过程：
同时，给出终极定义，什么叫支持向量？也可以理解为支撑向量，就是这些点支撑了w和b的存在。
写在最后：
ps:能看到这里的。。。我都觉得很佩服了，虽然学这个算法搞懂了大概算法步骤再写代码基本上就可以解决问题了，但是数学基础不能忘记，以后的学习笔记我也会尽量简洁一点，不扯那些复杂难搞的数学证明，但是另一方面，学好机器学习这些数学是有必要掌握的，所以课下多算算，就不写笔记了，毕竟很多数学公式的编辑要占用很多时间，有这些时间都可以去写代码了。
PS1:这一篇基本都是看书和看博客借鉴归纳得到，可能又会掉粉hhhh，看数学看不进去的童鞋，可以忽略本篇～
大家早睡，为了明日的继续学习，晚安～
以上是关于支持向量机的主要内容，如果未能解决你的问题，请参考以下文章