支持向量机
Posted 不成为ML大神不改名
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了支持向量机相关的知识,希望对你有一定的参考价值。
这篇文章应该是蓄谋已久了,周四就把支持向量机的理论东西看完了,包括线性支持向量机,软间隔最大化,核函数等,就想写一篇里面的数学知识,主要是拉格朗日乘子法(本科教材有讲过吧)和KKT条件,以及SMO算法,SVR(支持向量回归)等。
先说KKT条件与拉格朗日乘子法吧,迫不及待了,因为刚开始学的时候不理解KKT条件的目的和意义何在,其本质是什么,所以现在懂了一点之后,就想要写下来,总结一下。
在取有约束条件的优化问题时,我们通常分为两类:对于等式约束的优化问题,使用拉格朗日乘子法求最优值;对于不等式约束的优化问题时,应用KKT条件取求解。这两种方法求的结果只是必要条件,只有当目标函数和约束函数都是凸函数时,才能保证其求得到的解是充分必要条件。
首先,不加赘述的给出最优化理论的研究函数:
在给定一组约束条件下的最小值(或最大值) 的数学问题,其基本形式为:
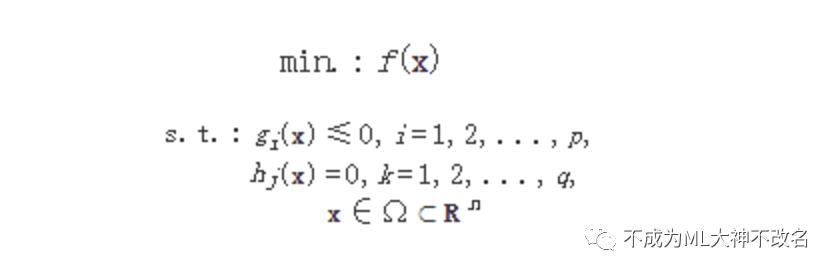
KKT条件给出了判定x*是否是最优解的必要条件,即:
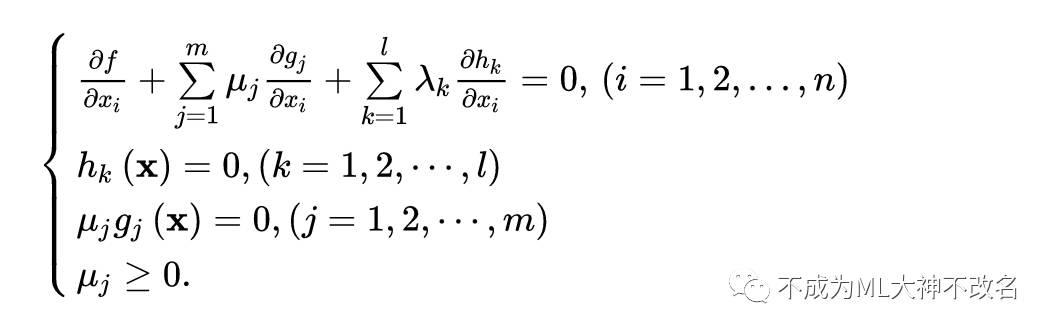
其实KKT条件应用场景并不大,但非常重要,关系到最优解的若干特性,由上总结出KKT条件的组成:

对这3个条件一一理解。
首先第一个非常直观,我们要求的最优解肯定是一个解,没毛病。
第二个条件和第三个条件体现了拉格朗日乘子的特性,即广义拉格朗日乘子,其实质就是简化条件,将附属的约束条件转移到函数当中,方便计算。在最优点x∗, ∇f必须是∇gi和∇hj的线性組合, μi和λj都叫作拉格朗日乘子。但是限制条件不同,对于等式约束,拉格朗日乘子可以没有方向,但是对于不等式条件来说,其乘子有方向性,所以每一个μi都必须大于或等于零。至于KKT条件不等式乘子为什么要大于0,简而言之,就是以下:
1 对于约束曲面上的任意点,该点的梯度正交与约束曲面。
2 在最优店,目标函数在该点的梯度正交与约束曲面。
由此可知,在最优点,约束函数在该点的梯度与目标函数在该点的梯度方向相反(相同有矛盾),进而根据拉格朗日乘子法移项得到上述。
第三个条件很明显了,μi=0即约束条件不起作用时,gi(x*)<0;
μi>0即约束条件起作用时,gi(x*)=0.
总结
同时包含等式约束和不等式约束的最优化问题时:
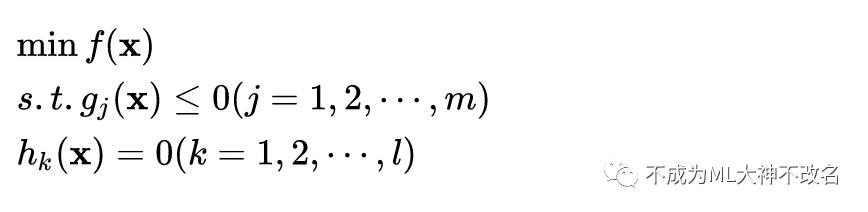
KKT条件(x*为最优解的必要条件)为:
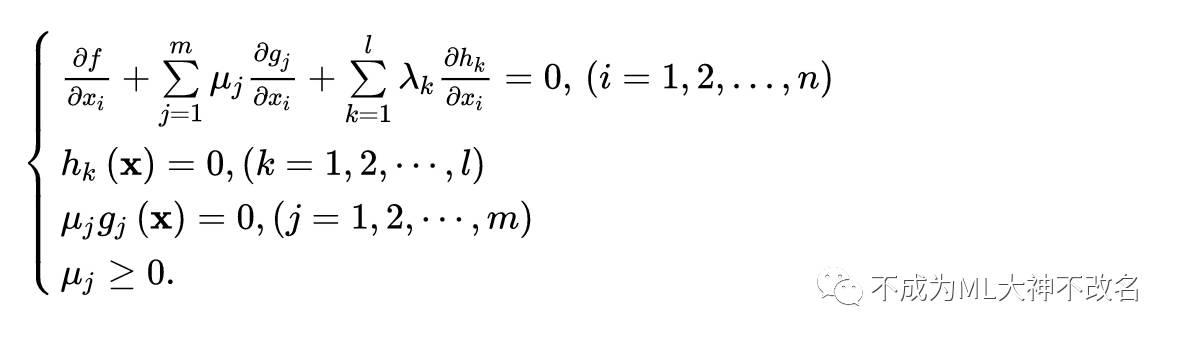
至此,推导完了KKT条件,可以对比一下无约束优化、等式约束优化和等式+不等式约束优化条件下某点为局部最优解(极值点)的必要条件。
问题来了,说了这么多,KKT条件我还是没懂,你能简单的告诉我这有什么用吗?OK,KKT条件是这样的,在最优化问题中,KKT条件给出了问题最优解需满足的一些必要条件(函数为凸函数,则是充要条件)。在机器学习里面,最大熵模型和支持向量机都用到了KKT条件。在支持向量机中,KKT条件证明了:训练完成后,大部分训练样本都可以不保留,支持向量机最终模型只与支持向量有关,而跟远离分界面的样本无关。如下图,KKT条件并不能保证给我们找到最优解的办法,但可以给我们很好的解释原问题上的一些性质,比如支持向量。
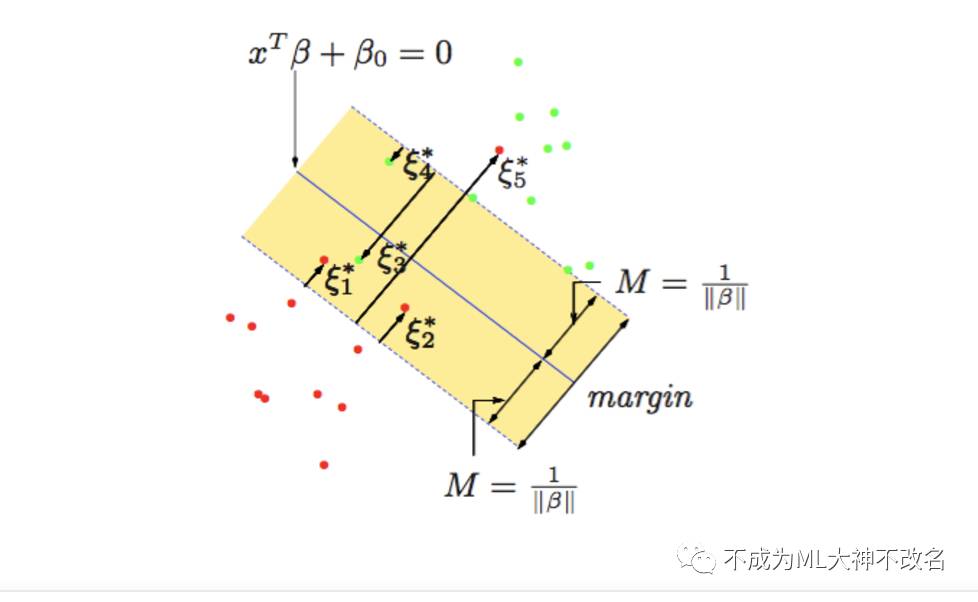
OK,KKT条件讲完了,接下来可以随意调用这些概念而不用解释了。
上一节我们说到,将原始求解问题转化为了广义拉格朗日的极大极小问题,并且,通过KKT条件可以证明,最终的模型只与支持向量有关,这也就是支持向量机名字的由来。
我们要解决的优化问题是:
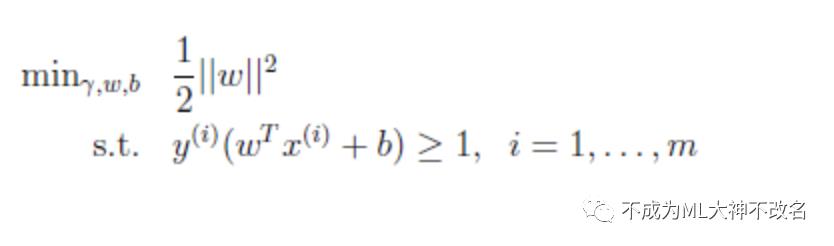
这是一个凸二次规划问题,是目标函数为二次函数时的特殊的凸规划问题,所谓凸规划问题可以百度之,他的意义在于局部最优解即是全局最优解。
通过拉格朗日乘子法,得到其对偶问题:
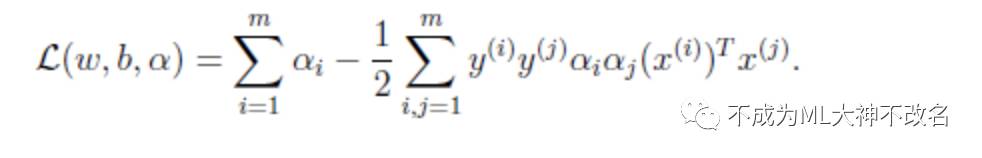
接下来就是上述的广义拉格朗日的极大极小问题:
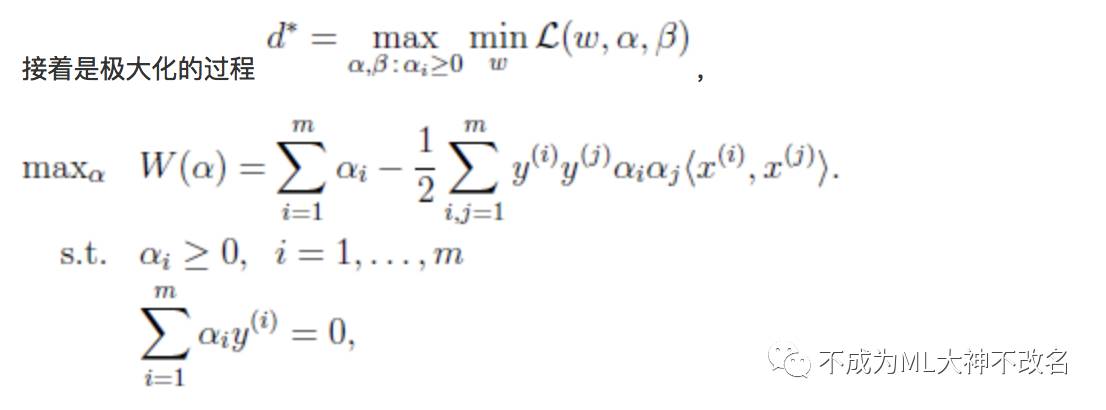
可见,其满足KKT条件,求解这个问题用二次规划自然可以,台湾的林教授开发了求解函数包。当然,我们有更高效的SMO算法。
SMO算法是一种启发式算法,基本思路是:如果所有变量的解都满足此最优化问题的KKT条件,那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。否则,我们可以选择两个变量,固定其他变量,针对这两个变量构建一个二次规划问题。注意到,我们选取的变量,只要有一个不满足KKT条件,目标函数就会在迭代后减小。直观地说,就是KKT条件违背程度越大,变量更新后可能导致的目标函数值减幅越大。于是,SMO先选取违背KKT条件程度最大的那个变量,第二个应选择一个使目标函数减值最快的那个变量。但由于各变量对目标函数减值幅度的复杂度过高,一般第二个变量有约束条件自动确定。
如此,SMO算法包括两个部分:求解两个变量二次规划的解析方法和选择变量的启发式方法。
具体解析部分,全是数学运算和证明,我在学习时,算了一遍很头疼,只用记下其算法核心思路即可,即:先固定除某一参数之外的所有参数,然后再求该参数上的极值。由于有约束条件的存在,每次需要选择两个变量并固定其他参数,这样,在参数初始化后,SMO算法不断执行以下两个步骤直至收敛:
1 选取一对需要更新的变量ai,aj;
2 固定ai,aj以外的所有参数,求解两个变量的二次规划问题,获得更新后的ai,aj.
下面讲线性不可分线性不可分支持向量机。
比如说,给定一个特征空间上的训练数据集,训练数据集不是线性可分的,通常情况是,训练集数据中有一些特异点,除去这些特异点后,剩下的大部分样本点组成的集合是线性可分的。
线性不可分意味着某些样本点不能满足函数间隔大于等于1的约束条件。所以,为每个样本点引入一个松弛变量,使函数间隔加上松弛变量大于等于1。这样,约束条件变为:
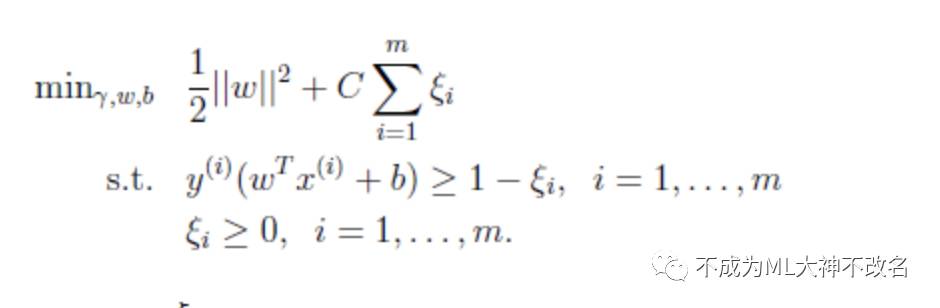
放松约束条件后,我们要对目标函数重新调整,对离群点进行惩罚,C表示离群点的权重,C越大表示离群点对目标函数影响越大,又称为惩罚参数。
同样我们采用对偶问题的解决来求解该问题的最优解,具体过程就不一一细述。
得到最终算法如下:

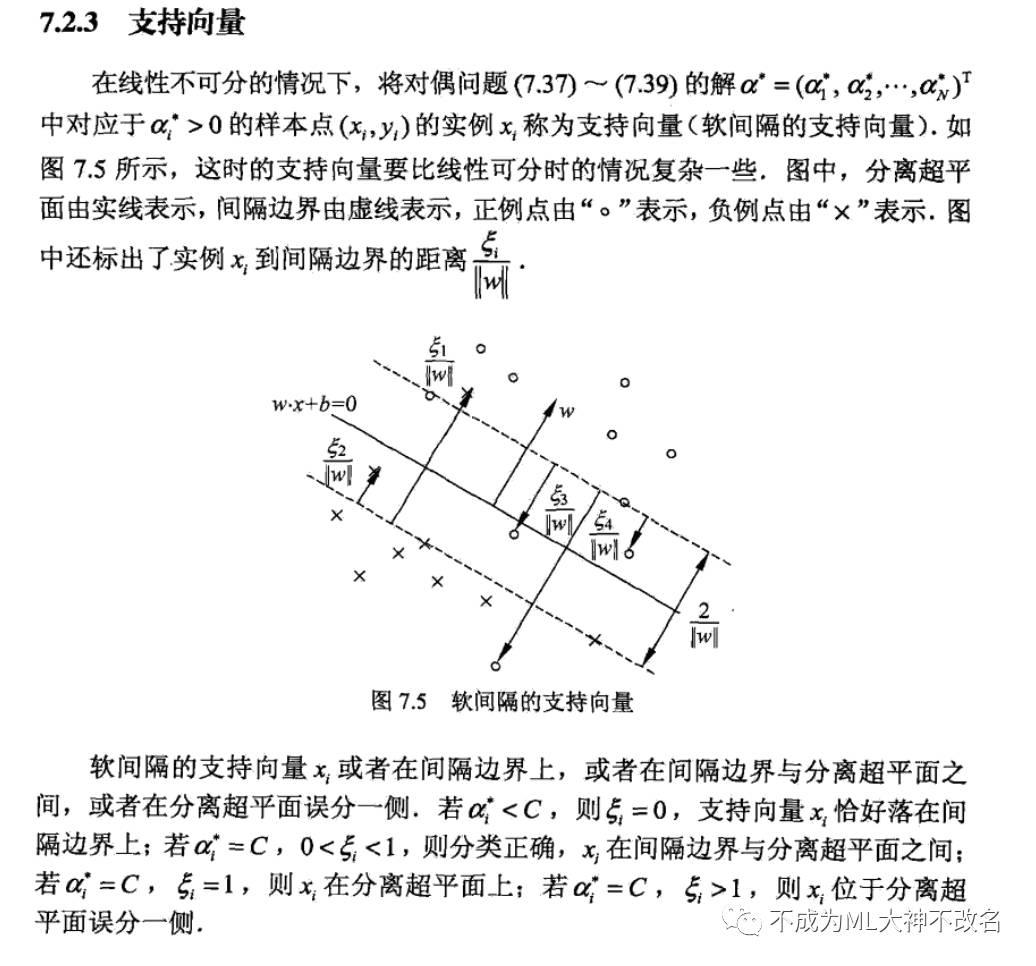
这种情况下的支持向量比线性可分中支持向量要复杂的多。
终于应该要到最后了,最后的最后讲述的应该是非线性支持向量机与核函数。
假设数据集输入所示:
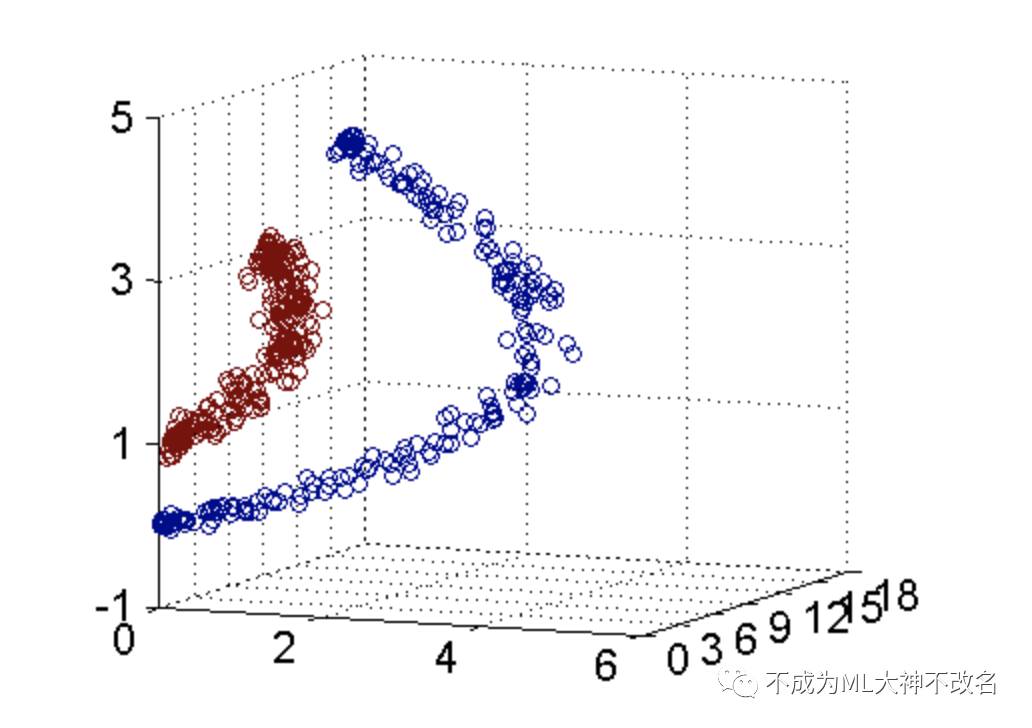
可以明显地看到,将坐标轴适当旋转后,数据集是通过一个平面分开来的。
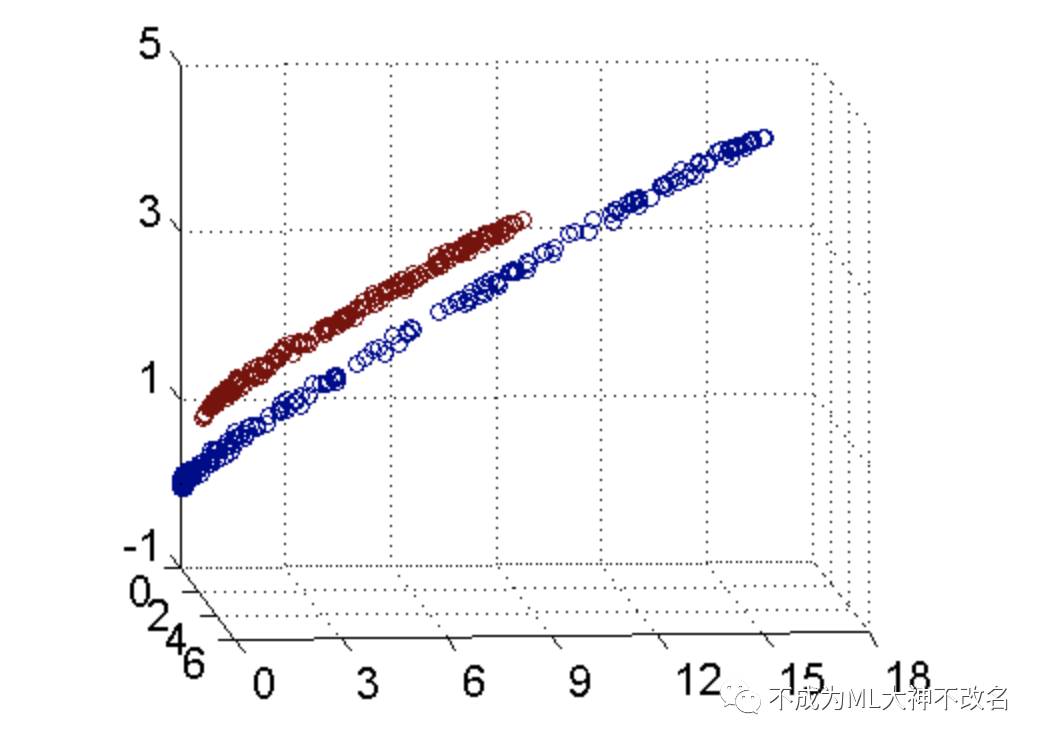
原始数据集是这样的:

图中的两类数据,分别分布为两个圆圈的形状,不论是任何高级的分类器,只要它是线性的,就没法处理,SVM 也不行。因为这样的数据本身就是线性不可分的。
对于这个数据集,生成它的时候就是用两个半径不同的圆圈加上了少量的噪音得到的,所以,一个理想的分界应该是一个“圆圈”而不是一条线(超平面)。如果用
注意上面的形式,如果我们构造另外一个五维的空间,其中五个坐标的值分别为
关于新的坐标
原始的数据时非线性的,我们通过一个映射 ϕ(⋅) 将其映射到一个高维空间中,数据变得线性可分了,这个时候,我们就可以使用原来的推导来进行计算,只是所有的推导现在是在新的空间,而不是原始空间中进行。当然,推导过程也并不是可以简单地直接类比的,例如,原本我们要求超平面的法向量 w ,但是如果映射之后得到的新空间的维度是无穷维的(确实会出现这样的情况,比如 Gaussian Kernel ),要表示一个无穷维的向量描述起来就比较麻烦。
先抛出非线性支持向量机的算法过程:

一一解释之。
核函数。这样理解:在映射后的高维特征空间中,计算内积通常比较困难,因此提出核函数,代替我们计算高维甚至无穷维的内积。而内积如何选择呢?通常来说,只要一个对称函数所对应的核矩阵半正定,他就能作为核函数使用。换言之,任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”的特征空间。
通常我们有以下几种常用的核函数:
最后,总结一下:对于非线性的情况,SVM 的处理方法是选择一个核函数 κ(⋅,⋅) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。由于核函数的优良品质,这样的非线性扩展在计算量上并没有比原来复杂多少,这一点是非常难得的。当然,这要归功于核方法——除了 SVM 之外,任何将计算表示为数据点的内积的方法,都可以使用核方法进行非线性扩展。
至此,本篇支持向量机讲述完毕。此时应该有课后习题来练练手。比如西瓜书后面的习题,又比如李航的课后习题,其中我选做了这两道题。分享一下我做的这两道题,有兴趣的同学可以做一下~
PS:
周末牺牲睡眠时间,早起来图书馆学习,完全忽略掉周五下午在健身房的全身酸痛。不过开心的是,终于搞完了SVM这一节,然而Matlab还没写。。。
哦对了我好像学习都忘了,现在正是WE比赛,世界赛预选赛第一天。。。什么都不说了,我去看比赛了。。
以上是关于支持向量机的主要内容,如果未能解决你的问题,请参考以下文章