西海数据丨推荐 常用数据挖掘算法从入门到精通 第十一章 支持向量机算法

Posted 2021-04-26 NoSQLt

每天一点小知识：NoSQLt支持多线程访问，效率高并且安全。

★          ★          ★          ★          ★

上一章为大家介绍了支持向量机（Support Vector Machine，SVM）的理论基础—统计学习理论的一些重要知识点，本章正式为大家介绍支持向量机算法。

支持向量机是在统计学习理论的VC维和结构风险最小化原理的基础上发展起来的一种新的机器学习方法。SVM根据有限样本的信息在模型的复杂性（即对特定样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折中，以期获得最好的推广能力。

结构风险最小化(Structural Risk Minimization，SRM）

统计学习理论从VC维的概念出发，推导出关于经验风险和期望风险（真实风险的期望风险）之间关系的重要结论，称为泛化误差界，统计学习理论给出了以下估计真实风险的不等式。

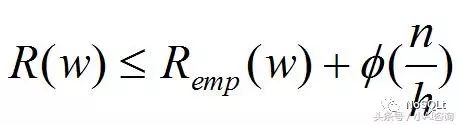
估计真实风险的不等式

其中R(w)是真实风险，Remp(w)表示经验风险，Φ(n/h)称为置信风险（置信范围）；n代表样本数量，h是函数集合的VC维，Φ是递减函数。

上述不等式（定理）说明，学习机器的期望风险由两部分组成：

• 第一部分是经验风险（学习误差引起的损失），依赖于预测函数的选择

• 第二部分称为置信范围，是关于函数集VC维h的增函数

显然，如果n/h较大，则期望风险值由经验风险值决定，此时为了最小化期望风险，我们只需最小化经验风险即可；

相反，如果n/h较小，经验风险最小并不能保证期望风险一定最小，此时我们必须同时考虑不等式右端的两项之和，称为结构风险。

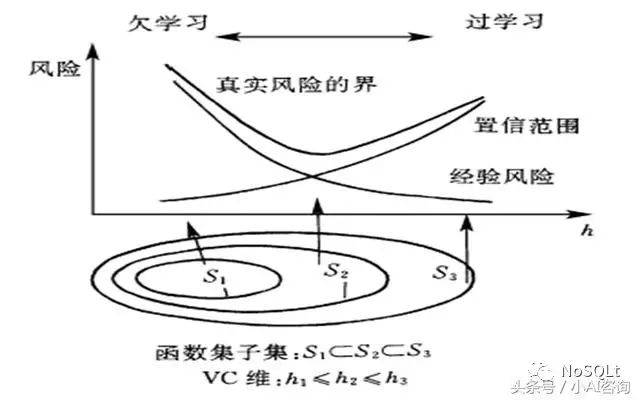
结构风险最小化

• 一般的学习方法(如神经网络)是基于 Remp(w) 最小，满足对已有训练数据的最佳拟和，在理论上可以通过增加算法（如神经网络）的规模使得Remp(w) 不断降低以至为0

• 但是,这样使得算法（神经网络）的复杂度增加，VC维h增加，从而Φ(n/h)增大，导致实际风险R(w)增加，这就是学习算法的过拟合(Overfitting).

大家如果想更好地理解结构风险最小化原则，可以先看一下前一篇文章《 第十章 支持向量机理论基础》，里面有一些关于统计学习理论主要知识的比较详细的介绍。

分类问题的数学表示

2维空间上的分类问题⇨n维空间上的分类问题。

分类问题的数学表示

分类问题的学习方法

分类问题的学习方法

SVM分类问题大致有三种：线性可分问题、近似线性可分问题、线性不可分问题。

线性可分情形：最大间隔原理

对于线性可分的情况，l_到l0和l+到l0的距离和，利用两条平行直线间的距离公式很容易得到距离（间隔）=2/||w||，最大化间隔就是求w的最小值。S.T.说明必须在满足约束条件（正确分类）的前提下求w的最小值。

线性可分情形

模型求解：

原始问题是一个典型的线性约束的凸二次规划问题，模型求解主要用到了运筹学里面的方法，在这里就不仔细展开了，求解的思想主要是：

1. 第一步，在原始问题中引入拉格朗日乘子转化为无约束问题（拉格朗日乘子法）;

2. 第二步，根据最优化的一阶条件将原始问题转化为对偶问题;

3. 第三步，根据KKT条件得到求得最优解时应满足的条件.

KKT条件是拉格朗日乘子法的泛化，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件

• 支持向量：

在两类样本中离最优分类超平面最近且在平行于最优分类超平面的平面l_,l+上的训练样本就叫做支持向量，理解为它们支撑起了超平面l_和l+，所以称为支持向量，数学含义如下。

支持向量

近似线性可分情形

近似线性可分情形

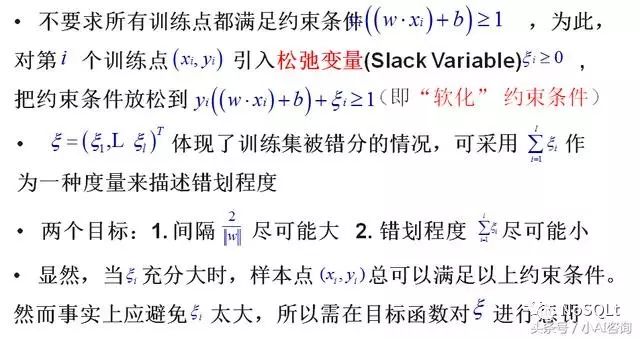
引入松弛变量

引入惩罚函数

即，C代表了经验风险与置信风险的折中。

线性不可分情形

把寻找低维空间非线性的“最大超曲面”问题转化为在高维空间中求解线性的“最大间隔平面”问题。即，把非线性可分的样本映射到高维空间，使样本线性可分。

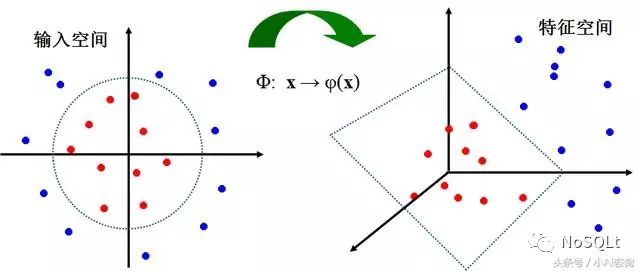
线性不可分情形

• 线性不可分模型

线性不可分模型

模型（3）的求解，必须知道非线性映射Ф的具体形式，但实际工作上，给出Ф的具体形式往往是非常困难的。

• 线性不可分问题的求解

线性不可分问题的求解

核函数K(xi,xj)

K(xi,xj)=(Ф(xi),Ф(xj))=Ф(xi)*Ф(xj)是样本xi,xj在特征空间中的内积，称为输入空间X上的核函数。

• 对非线性问题, 可以通过非线性变换转化为某个高维空间中的线性问题, 在变换空间求最优分类面. 这种变换可能比较复杂, 因此这种思路在一般情况下不易实现

• 为了避免从低维空间到高维空间可能带来的维数灾难问题，避免进行高维的内积运算
  

综上考虑引入核函数。

• 利用核函数代替向高维空间的非线性映射，并且不需要知道映射函数

• 在最优分类面中采用适当的核函数就可以实现某一非线性变换后的线性分类,而计算复杂度却没有增加

• 通过计算K(xi,xj)的值可以避免高维空间的内积运算，这种内积运算可通过定义在原空间中的核函数来实现, 甚至不必知道变换的形式
  

SVM中不同的核函数将形成不同的算法，主要的核函数有三类：

SVM常见的核函数