Computer Vision | SVM loss function支持向量机损失函数在线性分类器中的应用

Posted 2021-04-26 夏至又一年

小姐姐虽然大学时学的是模式识别信号处理，但是当时学的很浅，后来在美帝学的是数值计算，现在又回到计算机视觉的领域，发现数值计算的基本思想居然跟图像处理是相通的！现在机器学习里面考虑的几个主要因素：计算精度、计算效率、误差项收敛速度、迭代前初始条件和边界条件的设置、防止多项式高阶项的过拟合等等。。。都有异曲同工之妙，每往前深入一点，都有一种“原来知识都这么相通啊”的奇妙感觉！

另外小姐姐今天在看训练数据过拟合这个问题的时候，发现里面提到一个 “Occam's Razor 奥卡姆剃刀原理”。听说是一个14世纪的英国逻辑学家叫William的，他住在一个叫Occam(奥卡姆)的地方，然后他提出了这个理论，中文翻译为“如无必要，勿增实体”。

就是说如果关于同一个问题有许多种理论，每一种都能作出同样准确的预言，那么应该挑选其中使用假定最少的。尽管越复杂的方法通常能作出越好的预言，但是在结果大致相同的情况下，假设越少越好。我一看这不就是小姐姐前几天刚刚说过的“至繁则至简”吗！我就惊呆了，就这么一句话也能成为原理吗我要回到14世纪去做科学家，说不定还有机会认识赵敏郡主

一不小心暴露年龄了好言归正传，开始写loss function~

---

上一篇的末尾我们提到因为Linear Classification最重要的参数是权值矩阵W，那么怎么让权值矩阵得到正确的取值，成为影响线性分类器最重要的指标。比如如果我们的算法得到以下的结果：

对小猫咪这张图cat这个分类算出来是2.9，另外还有deer，dog和frog分都比它高，说明这个结果一般般；而小车车算出来的分6.04是所有类别里面最高的，可以说表现得很好；最后小青蛙算出来了负分（滚粗）！那真的是很糟糕。

所以量化输出结果有多糟的函数，就叫做loss function损失函数。然后这个遍历所有可能的权值取值最后得到正确取值的过程，就叫做optimization procedure 优化过程。

下面我们用更简化的例子来具体计算，只取3个训练样本，3个分类：

x代表图像的像素值，y代表目标（也称为标签），y是一个0-9的整数（也可能是1-10，看你用哪种编程语言），当然在这里是一个0-2的整数，因为只有3类。

那么损失函数L就可表达为如下图所示：

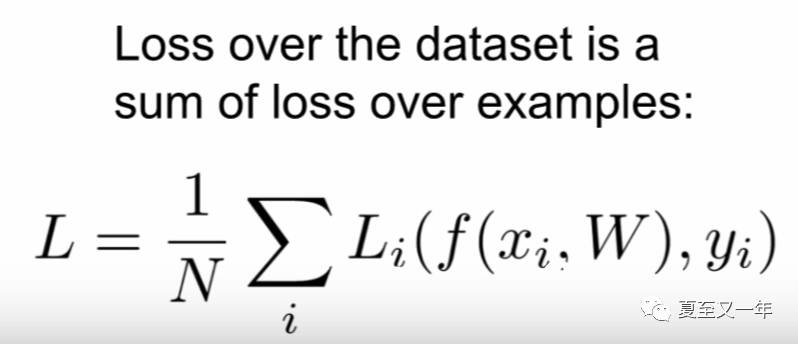
将f(xi,W)算出的预测值和真实的标签进行某种运算，然后基于整个数据进行求和平均，得出一个量化标准来衡量预测结果到底好不好。

下面我们讲到的一个具体的损失函数，叫做multi-class SVM(support vector machine) loss多类别支持向量机损失函数。支持向量机SVM本来是一个二元线性分类器，只能判断是或者不是（0或者1），这里将它的功能更泛化了一点，使之能够进行多于两个以上的类别的分类判断，所以叫multi-class。其表达式如下所示：

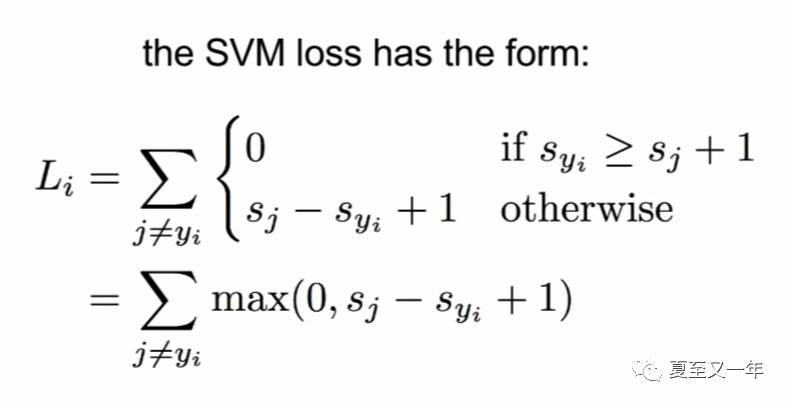
其中是分数向量。

它对除正确分类外的所有分类（j != yi）求和，以比较正确分类预测值Syi和错误分类预测值Sj之间的差值，同时设置了一个安全边界量1，如果正确类别预测值Syi比错误类别预测值Sj再加1还大，那就说明它算得真好，没有损失，Li=0，除此之外的话就Li就等于其真实的差值（Sj-Syi+1）。最后一个等号后面的表达式是将条件表达式整合在一起的更简洁的表达，每次计算结果取0和差值之间更大的那个数。

它的函数画出来如下图所示，称为hinge loss（真的翻不出来，长得像合页的一样的损失函数？）可能因为它是折线形的吧。当正确类别的预测值比其他预测值都大很多的时候（大于安全边界量），那说明我们可以安全地预测当前图片的类别；当不足够大的时候，就会有损失产生。从下图可以看出，当hinge loss取值为0之后，就表示我们对这个例子正确分类了。

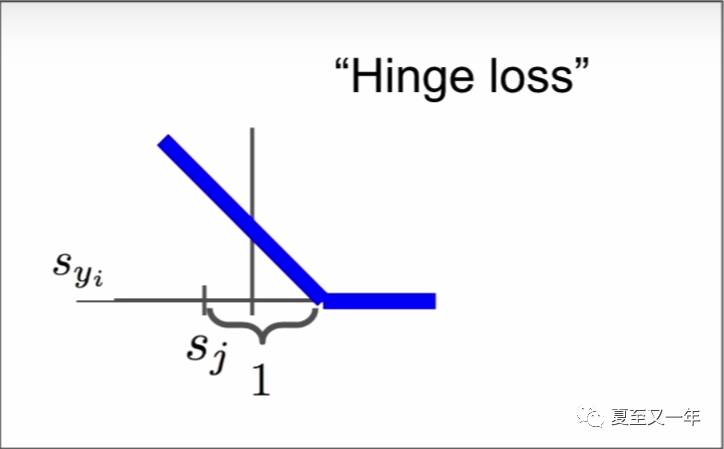
我们可以对那个只有3个训练样本，3个分类的简化例子进行具体的计算，先分析对小猫咪的预测：

小猫咪的正确分类cat的预测值是3.2，那么我们用它和错误分类car的预测值5.1进行比较，如果差值大于1就说明算得好，损失为0，如果小于1就说明有问题，有损失，损失值就是算出来的差值（可以看出来cat和car的差值是小于1的，3.2-5.1=-1.9，所以结果不够好，有损失，这也跟我们的直观判断一致），然后差值用公式计算Sj-Syi+1=5.1-3.2+1=2.9。

同理也对错误分类frog的预测值-1.7做同样的操作（cat和frog的差值大于1，3.2-(-1.7)=4.9，所以损失为0），最猫咪的损失值car损失值和frog损失值之和，L(car)+L(frog)=2.9+0=2.9。具体计算过程如下所示：

然后同理可以分析对小车车的预测：

小车车的总损失量为0，从直观也可以看出我们可以很自信地预测这张图片是车。

最后分析对小青蛙的预测：

小青蛙的总损失量为12.9，预测错误。

最后我们对这个算法进行求和平均，得出这个算法基于此次训练数据预测结果的总损失量为5.27（可以说我们对这个算法的糟糕程度进行了量化，它的糟糕程度是5.27）。

最后关于安全边界量为什么设置为1，因为我们其实不关心预测值的绝对值是多少，我们只关心预测值之间的差值是不是足够大，所以安全边界量的值具体设置为几是不影响结果的，在计算推导过程中它们都会被抵消掉（传说中深度学习deep learning这门课里面有对安全边界量取值不影响结果的具体推导证明过程，等我看懂了再写。。。）

在numpy的实际操作中，当对损失函数Li向量化的时候有一个小小的trick，就是对margin初始化的时候就把正确分类y的margin设为0，这样做迭代时候就自动剔除了它。

然后我们需要对multi-class SVM loss function做一些分析，通过一些问题的形式来具体回答。

Q1：如果小车车的预测值4.9变小了一点点对SVM loss有没有影响？

A：没有。因为SVM loss关心的是正确分类预测值与错误分类预测值的差值，因为car预测值跟别的比起来已经蛮大的了，所以在这里只要它们间的差值大于1，损失函数就可一直为0。

Q2：SVM loss的最大值和最小值分别为多少？

A：我们重新看一下hinge loss那张图。

可以看到最小值是0，最大值可以为无穷大。

Q3：如果在权值矩阵W初始化的阶段，所有的分数向量s=f(xi, W)都约等于0，而且差值都很小的话，那么它的SVM loss会是多少？

A：Li = 类别数 - 1。

在初始迭代时期，如果各预测值之间差异不大的话，那么差值就为Sj-Syi+1=1，又由于是在除了正确分类之外的其他数据上求和，那结果就为类别数C-1。

这是一条非常实用的debug策略，在完成第一次迭代以后，可以通过观察其SVM loss是不是等于C-1来判断代码有没有问题。

Q4：如果我们基于所有类别求和，而不排除正确类别的话（including j=yi），SVM loss会有什么变化？

A：Li = Li + 1。

根据差值公式Sj-Syi+1=1，当 j = yi 的时候，差值为0，于是总损失量+1。不过其实因为做循环的时候包不包含正确分类都不会影响最后的预测值，所以为了减轻计算量的负担，我们就不包啦。

Q5：如果我们用均值来代替求和，SVM loss会有什么区别？

A：没差。因为类别数是固定的，所以用均值来代替求和只是让损失函数从乘以一个常数变成了乘以另外一个常数，而这些常数最后都会被抵消掉，不会对实际预测值产生影响（这应该也是安全边界量取值多少都没关系的原因，等我再研究研究~。。。）

Q6：如果我们改用平方值来算损失量，它还会是同一个问题吗，还是变成了另外一个算法？

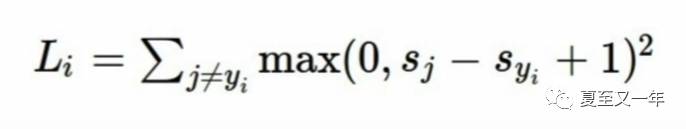
A：那这就完全变成了另外一个分类器啦，因为SVM loss是用线性函数来衡量预测结果的好坏，平方之后就不再是线性函数啦。

另外因为取平方值会放大误差，所以采用哪一种损失函数也代表了你的算法更在乎哪一种误差，而哪一种误差可以牺牲掉用以换取别的性能的提升。

Q7：假设你已经找到了一个权值矩阵W可以使得损失量为0，那么这个W唯一吗？

A：不唯一。如果有W使得Li = 0的话，那么 2W 的 Li=0。不信我们回到上面小车车的例子，如果W变成2W的话，说明预测值的差值也会翻倍，所以把它们的差值都放大一倍来重新算一下损失函数。

可以看到因为本来的差值就大于1，翻倍之后更加大于1，所以不会损失函数的值不变。

那这样就引申出另外一个问题，如果同一个损失函数能选出这么多个权值矩阵W的话，那么我们到底选哪一个呢？以及为什么会产生这种情况呢？

这是因为到目前为我们的衡量标准都停留在关注训练数据上面，但是前面我们已经提过了衡量一个算法的性能是不在乎它在训练数据上面的表现的，我们更在乎的是它在训练完成以后在测试数据上面的表现。所以要小心在这种损失函数的指引下我们可能让算法走入一个奇怪的境地，它会产生出一些不太直观的行为。

我们可以从另外一个角度来解释这个问题。假设我们需要通过下图这些已知的蓝色数据点（训练数据）来拟合出一个函数，用以预测绿色数据点（测试数据）的标签。

如果我们用一个高阶多项式（蓝线）来完全覆盖住每一个训练数据的话（这就是衡量标准都停留在关注训练数据上面），那么对绿色的测试数据来说不一定是好事，它有很大概率会产生误判。

相反如果用一个线性函数（绿线）来拟合的话，虽然并没有让每个训练数据都落在这条线性函数上，但是它却能对预测数据做出更正确的判断。

这是机器学习中的一个核心问题，叫做overfitting problem(数据过拟合)，我们解决的办法就是在损失函数中引入regularization term(正则项)。

好！终于可以收篇了！下一篇写正则项！！