支持向量机算法

Posted 2021-04-26 数据科学与人工智能

 摘要 

本文主要讲机器学习中一个非常重要的二类分类模型：支持向量机（Support Vector Machines）。文中主要讲解了SVM的三种模型：线性可分支持向量机、线性支持向量机、非线性支持向量机，重点讲解该模型的原理，及分类决策函数的计算推导过程。

引例小视频

基本方向

首先，SVM不能通过“支持向量机”字面意思来理解。其次，SVM是机器学习中很经典的一个二类分类模型。分类的最终目的是找到样本之间的一条分界线，然后用新样本点和分界线的关系，来判断类别。这是我们的基本思想。

在前面，我们已经学习了一个很基础、很经典的二类分类模型：

那么，SVM和感知机之间又有什么关系呢？

让我们先简单回顾一下感知机。

假设，我们有如下训练数据集T：

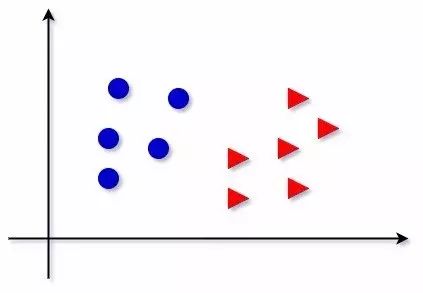
对于感知机来说，我们可以找到无数个超平面S（直线S），正确地对图中的数据集进行划分：

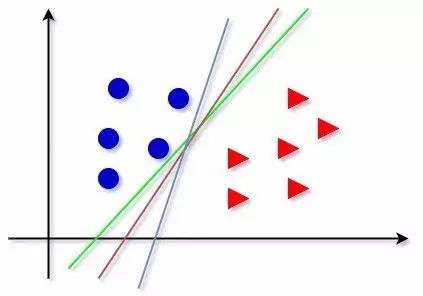
但是，在所有的划分超平面中，有一个平面是最好的，它可以尽最大可能地让所有的样本点都离得该划分平面最远，这就是SVM想要做的。

虽然，有无数个超平面可以对样本集进行划分，但是，不可否认，下面的这条直线应该是最优的：

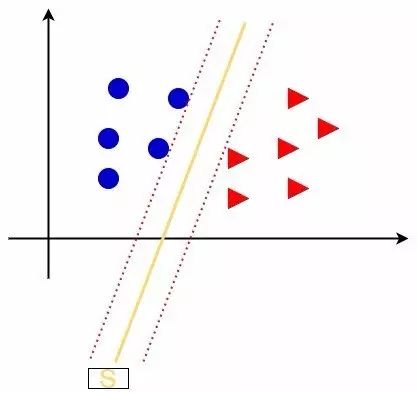
上图中的S使得两类样本点之间的间隔到达了最大，这条S就是我们在SVM中力求需要找到的，而这个特点也使得SVM有别于感知机。

支持向量机学习模型包括（由简到繁）：

1、线性可分支持向量机

这是一类最简单的支持向量机模型，它要求训练数据集是线性可分的，如上图中给出的训练数据集就是线性可分的。

2、线性支持向量机（不可分）

这类模型不要求训练数据集线性可分，但还是通过第1类的方法来做。

3、非线性支持向量机

这是最复杂的支持向量机，它的训练数据集本身是非线性的，但是通过线性变换，我们可以将这个数据集投射到另外一个特征空间，在新的特征空间中训练数据集变为线性可分。而这其中使用了一个非常重要的概念，叫做核技巧（Kernel Trick）。

以上就是支持向量机的一个基本方向，我们的大致路径和前面感知机的分析方法一样，通过假设空间，确定损失函数，然后通过求损失函数的极值来确定对应参数。

那么，接下来就一起来具体学习吧。

线性可分支持向量机（定义、函数间隔、几何间隔）

一般滴，当训练数据线性可分时，存在无数多个分离超平面可以将两类数据正确分开。感知机利用误分类最小的策略，求得分离超平面，不过这时的解有无穷多个。线性可分支持向量机利用间隔最大化求最优分离超平面，这时候，解就是唯一的。

• 定义

给定线性可分训练数据集，通过间隔最大化或者等价求解相应的凸二次规划问题学习得到的分离超平面为：

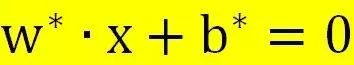
相应的决策函数为:

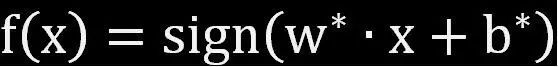
目前，根据线性可分支持向量机所要完成的任务，得到了对应的定义。那么，接下来，我们要解决的问题是：如何确定上面的分类决策函数中的w和b。

在这里，我们使用的是最大间隔法，但是在讲最大间隔法之前，我们还必须掌握两个基本的概念：函数间隔和几何间隔。

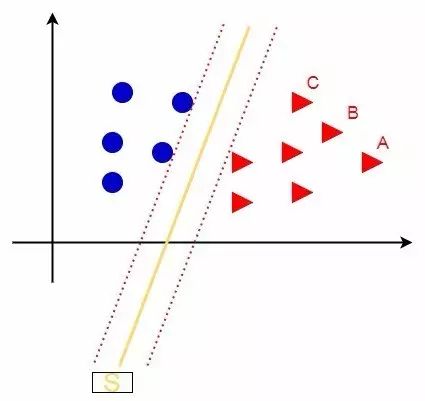
如上图所示：我已经找到了分离超平面S，对于A,B,C三个点全部落在了分离超平面的同一侧，说明A、B、C属于红色三角形这一类。但是，我们需要确定，对于A、B、C来说，他们的确信程度到底有多高呢？

首先对于A点来说，到S的距离是最远的，所以，我们可以说A点的确信度最高，其次是B，而因为C点距离分离超平面S很近，所以，C点的确信度最低。

由此可见，我们可以通过一点到分离超平面S的距离来衡量该点的确信度。

在超平面 wx+b=0 确定的情况下，我们可以用 |wx+b| 相对地表示点x到分离超平面的远近，而wx+b的符号与类标签y的符号是否一致可以表示分类的正确性。所以，我们可以用 y(wx+b) 来表示分类的正确性及确信度。我们将这个量叫做函数间隔。

• 函数间隔

假设有训练数据集T和超平面S （w,b）。

超平面S关于一个样本点（xi,yi）的函数间隔为：

超平面S关于所有样本点T的函数间隔为：

在预测分离超平面的时候，只有函数间隔是不够的，我们还需要引入另外一个概念，几何间隔。

我们上面说了函数间隔只能相对地表示点到超平面的远近，而几何间隔便是真正点到超平面的距离。

为此，我们先复习一下点到直线的距离公式：

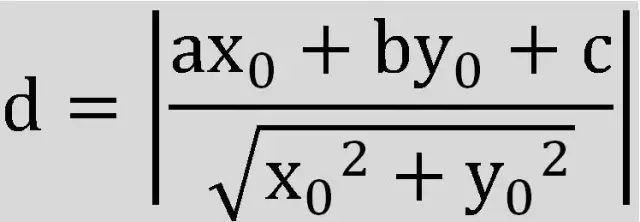
可见，函数间隔实际上就是距离公式的分母部分，而几何间隔就是距离公式。

• 几何间隔

  假设有训练数据集T和超平面S （w,b）。

超平面S关于一个样本点（xi,yi）的几何间隔为：

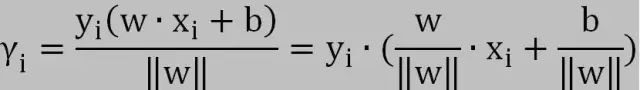
超平面S关于所有样本点T的几何间隔为：

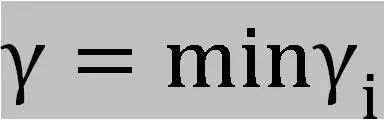
最后，我们可以得到函数间隔和几何间隔之间的关系为：

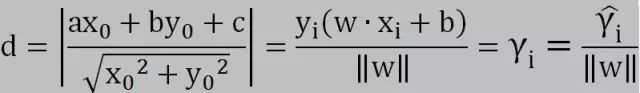
接下来，我们就可以用最大间隔法来解决线性可分支持向量机中确定w和b的问题了。

硬间隔最大化（最大间隔法、对偶算法、支持向量和间隔边界）

• 最大间隔法
  

根据以上线性可分支持向量机中的介绍，我们希望找到一个超平面，这个超平面距离所有的样本点都是最远的，也就是我们要找一个最大的几何间隔值，使训练数据集T的几何间隔大于等于它。即：

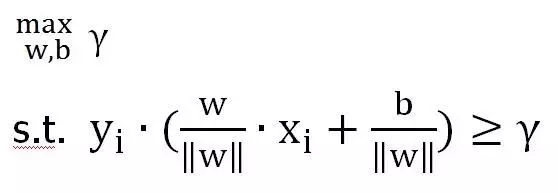
以上公式是使用几何间隔来表示，因为我们已经知道了几何间隔和函数间隔的关系，所以，我们可以将函数间隔带入公式：

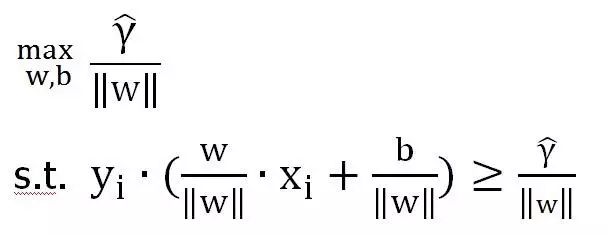
而函数间隔的取值并不影响上面的求解，所以，我们令函数间隔为0。问题就转化成了：

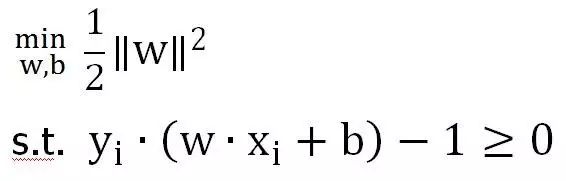
目前，我们的问题集中在如何解上面的式子上。

为了解决上面这个问题，我们引入了对偶算法。

• 对偶算法
  

对偶算法是应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解。

在上面小节中，我们已经得到了使用最大间隔法求解最优化的最后形式：

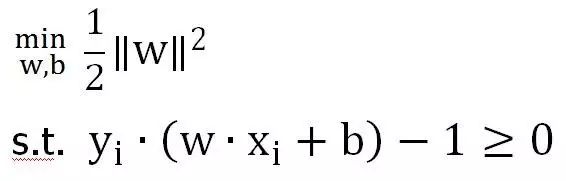
现在，我们利用多元函数求极值的方法：拉格朗日乘数法。

这样，我们就需要构造一个辅助函数：

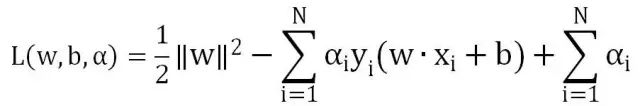
这样，我们的原始问题就变为了以下问题的求解：

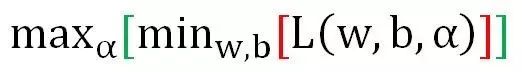
我们得到了关于w，b，a的函数L，分别对w和b求导：

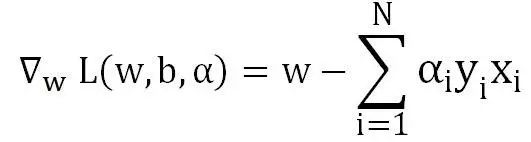
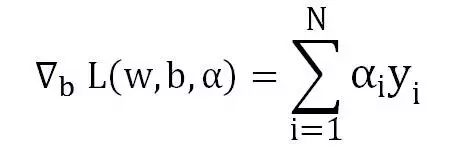
令对应偏导分别为0，则：

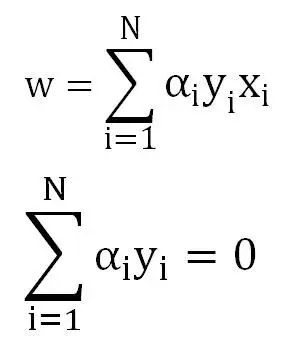
将上式带入原来的L函数即可得到L函数极小值的形式：

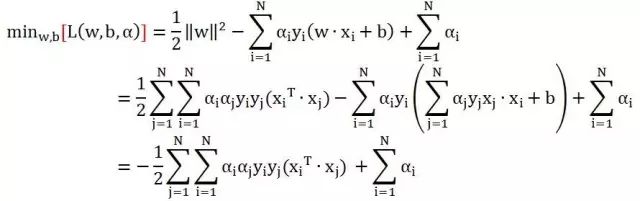
这样，上面的问题：

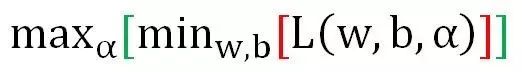
就等价于求解：

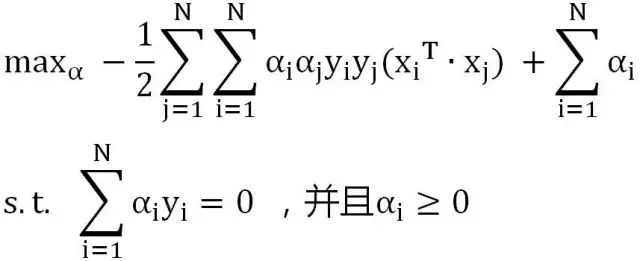
继续等价于求解：

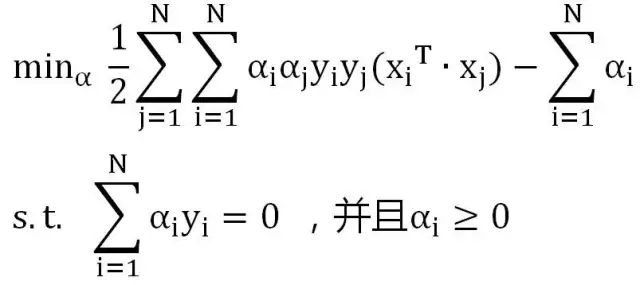
根据上面的式子，我们可以得到关于α的方程，以及约束条件，这样就可以将α求出，由此就可以得到w和b的值分别为：

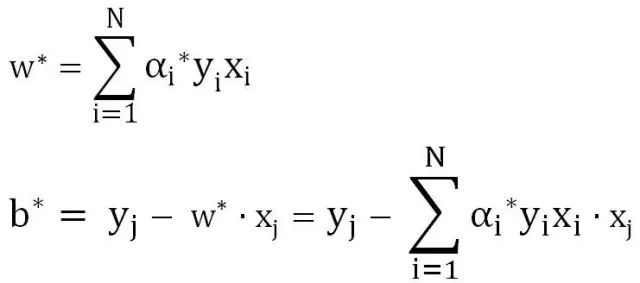
以上，就是对偶算法的核心思想。其实就是利用拉格朗日乘数法解决约束条件下多元函数极值的问题（参见张宇《高等数学18讲》）。

• 支持向量和间隔边界
  

最后，我们引入两个简单定义。

支持向量：在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量（support vector）。可见，只有少量的样本点决定了分离超平面。

（我会把support vector翻译为支撑向量，可能更形象化）

间隔边界：如上图S左右的两条虚线，即为间隔边界。

线性支持向量机

假设训练数据集不可分，有一些“特异点”，将这些特异点除去后，剩下大部分的样本点组成的集合是线性可分的。这时候，我们就使用线性支持向量机。

线性支持向量机学习仿照前面的线性可分支持向量机，上面我们所使用的间隔最大化，叫做硬间隔最大化，在这里，我们使用软间隔最大化寻找对应的分离超平面。由于实现以及求解算法和线性可分支持向量机类似，故这里不再阐述。

具体细节可参考李航的《统计学习方法》中7.2一节的精彩讲解。

非线性支持向量机

以上，我们解决了线性可分条件下的支持向量机算法，现在，我们看非线性。

回到我们引例中的视频，虽然有时候我们的训练数据集是非线性的，但是，我们可以通过线性变换映射到更高维的空间中去，以前非线性的样本居然就变为线性的了。

如下图所示：我们在原空间中的样本点是不可线性分割的，有一个椭圆函数可以将其分割开：

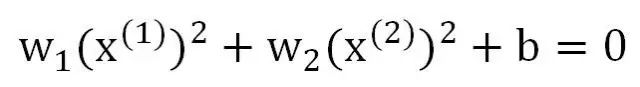
假设我们有一个变换：

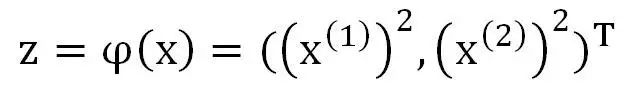
这样就可以变换成为新空间中的直线：

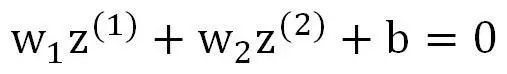
原来我们的训练数据集是不可线性分割的，但经过线性变换后，就可以分割了。这样就把非线性训练数据集转化为了可线性分割的训练数据集。如下图所示：

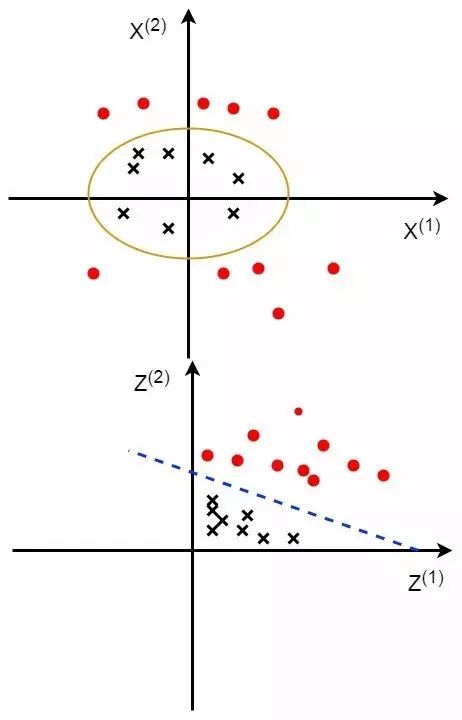
我们在这里整理一下非线性支持向量机的思路：

因为所给训练数据集T是非线性分割的，所以，我们希望通过一个线性变换M，将T转化到另外一个空间中，在那个空间中，所有数据集T线性可分，那么，我们就可以使用上面的线性可分支持向量机进行求解；但是，最为重要的是：求解完成后我们希望将得到的超平面S，通过线性变换M的逆变换，使S还原到原来的空间中。这其实和相似矩阵有点类似。

我们还能记得在线性可分支持向量机中，最后得到的式子为：

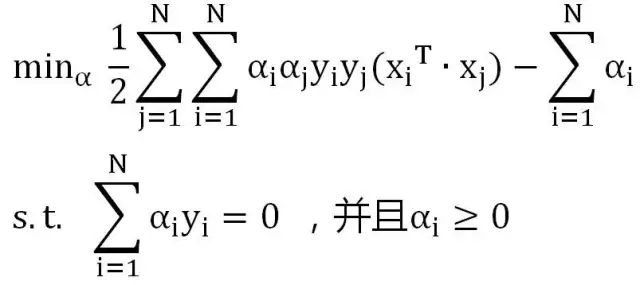
现在，我们假设有一个训练数据集T，是非线性的。

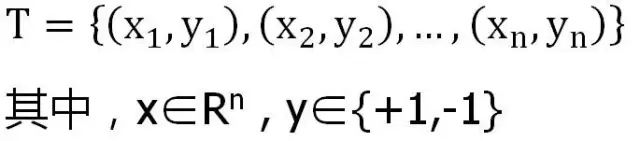
我们通过线性变换，将其变换到另外一个空间Z中：

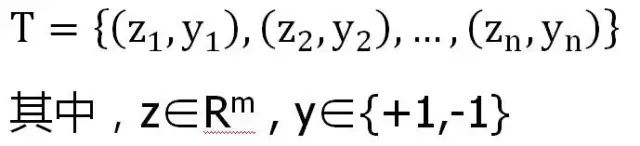
如果在空间Z中，T线性可分，则：

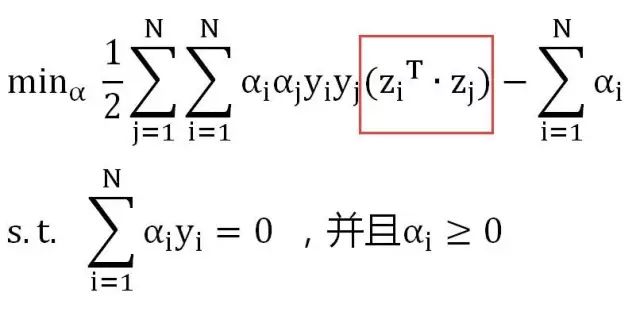
我们这里重点看一下上图中红色框内的部分。它表示在Z空间维度上两个向量的内积。

而Z和X有一下关系：

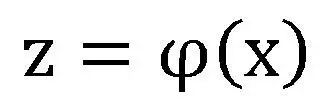
我们在做线性变换的时候，通常是由低维度向高维度转换，那么我们是不是可以用低维度向量之间的运算来表示高纬度向量的内积呢？

这就是，核技巧（Kernel Trick）。

• 核技巧

假设我们有这样一个函数：

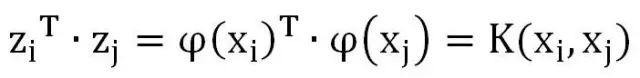
等式左侧为Z的内积，等式右侧为关于X的一个函数K，我们把K叫做核函数。

这样，在核函数给定的情况下，可以利用上面解线性可分情况的分类问题来求解非线性分类问题的支持向量机。

小结

以上对支持向量机的几种不同模型进行了简单介绍，我们重点掌握的是间隔最大化算法，以及核技巧的概念。

祝玩得开心！

参考资料

• 《统计学习方法》 - 李航

• 《机器学习》 - Youtube

• https://www.zhihu.com/question/30371867

• https://www.zhihu.com/question/21094489

---

文章推荐：

1

2

---

阅读原文，更多精彩！

分享是收获，传播创价值！