机器学习（04）：SVM支持向量机

Posted 2021-04-26 工业与数据的那些事

内容摘要

本文介绍了分割超平面的概念，推导出了SVM的目标函数，并采用拉格朗日乘子法将原函数转化为对偶函数进行求解；同时还对核函数进行了解释，最后利用SVM训练一个判别不同气体类型的分类器。

1. 分割超平面

什么是超平面？超平面在二维空间是一条直线，在三维空间是一个平面，我们上节的逻辑回归部分提到的决策边界实际上就是一个超平面。如果一个超平面可以把我们的样本集划分为两部分，则称之为分割超平面。如下图所示，分割超平面为w Φ(x)+b=0，其中Φ(x)是某个确定的特征空间的转换函数，它的作用是将低维的特征x映射到更高维度，在下图中Φ(x)= x：

当样本点落在分割超平面的法线的正方向，即w Φ(x)+b >0时，记为正例，y=+1；当样本点落在分割超平面的法线的负方向，即w Φ(x)+b <0时，记为负例，y=-1。这是我们希望分割超平面在测试集上的分类器效果。

为了提高分类器在测试集上的泛化能力，我们希望分割超平面在训练集上有着更强的分类能力，即希望训练集的样本点都落在分割超平面的两边，并且分的越开越好。因此我们针对训练集的分类器调整为：当样本点落在分割超平面的法线的正方向，即w Φ(x)+b >1时，记为正例，y=+1；当样本点落在分割超平面的法线的负方向，即w Φ(x)+b <-1时，记为正例，y=-1。

如上图所示，我们将w Φ(x)+b=1称为上边界，w Φ(x)+b =-1称为下边界，上下边界之间的区域称为过渡区，刚好落在上、下边界上的样本点称为支持向量（supportvector），上下边界之间的间隔称为分割间隔。

我们的目标是得到一个分割超平面，使得其分割间隔越大越好，这样的分类器鲜果越好。

 

2. SVM目标函数

根据上面的介绍：当w Φ(x)+b >1， y=+1；当w Φ(x)+b<-1，y=-1。为了简化处理，我们将两个式子合并为一个等价的式子来表达：y(wΦ(x)+b)-1>0。当样本点刚好落在分割超平面的上下边界上时，有y(wΦ(x)+b)-1=0。

为了得到更好的分类器，我们希望分割间隔越大越好。那怎么度量分割间隔呢？通过下图的示意可以看出分隔间隔就是上、下边界之间的距离，即上边界上的点到超平面的距离 + 下边界上的点到超平面的距离：

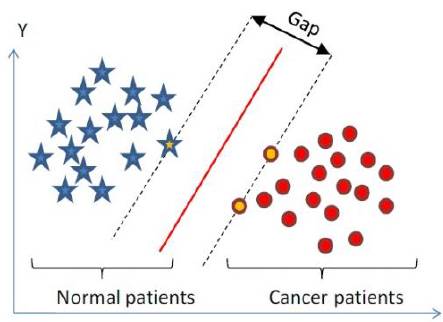
根据点到超平面的距离公式，边界上的点到超平面的距离为|w Φ(x)+b|/||w||。对于边界上的点（即支持向量）有y(w Φ(x)+b)-1=0，所以有|w Φ(x)+b|=1，因此边界上的点对超平面的距离为1/||w||，分隔间隔gap则是两倍的1/||w||。由此得到分割间隔的度量公式，即目标函数：

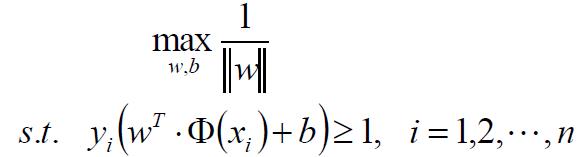
由于1/||w||不是凸函数，不方便求极值，因此将其转换为等价的目标函数：

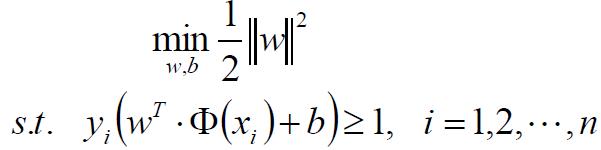
3.用拉格朗日法求带约束条件的极值问题

由于我们的目标函数是带有约束条件的，因此采用拉格朗日乘子法，将目标函数和约束条件写在一起：

上式中α为大于0的系数，而y(w Φ(x)+b)-1>=0，因此α(y(w Φ(x)+b)-1)总是>=0，所以有L(w,b,α)<= ½||w||²。换句话说，L(w,b,α)的极大值等于½||w||²，即max L(w,b,α)= ½||w||²。因此，原目标函数min ½||w||²等价于下面的极小极大值问题：

根据实践证明，极小极大值问题近似于其对偶问题，即极大极小值问题：

那我们现在的目标是转化为求解该对偶问题。为了求解对偶问题，我们首先求极小值min L(w,b,α)，分别对w,b求偏导并令其为0：

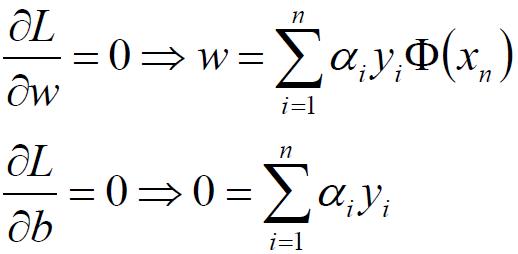
将上面两式带回到L(w,b,α)函数中：

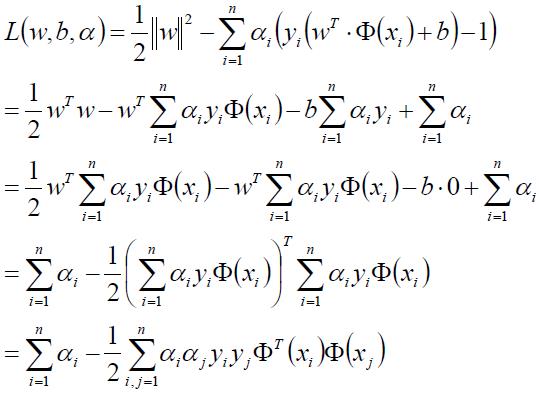
接下来我们继续求min L(w,b,α)对α的极大值：

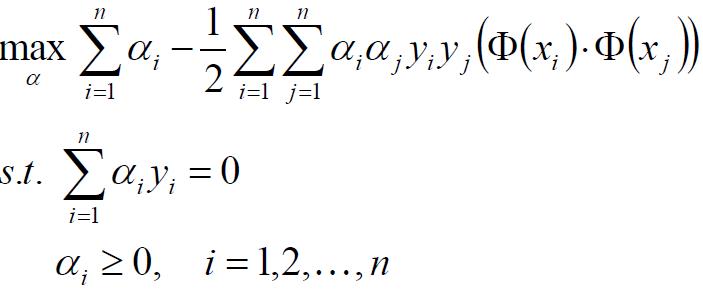
我们通过SMO(Sequential Minimal Optimization)算法求出参数w*和b*：

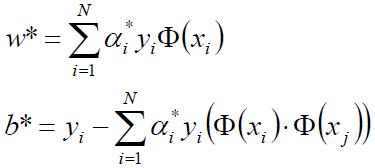
进而可以得到分割超平面w* Φ(x)+b*=0，然后根据测试样本点落在分割超平面的正方向还是负方向，预测为正例（+1）还是负例（-1）。

 

4. 隐变量α的理解

在上面的拉格朗日函数L(w,b,α)中，我们引入了约束条件α>=0。经过实例证明，当α>0时，则该样本点一定是支持向量；当α=0时，则该样本点不是支持向量。因此，我们可以理解为，只有支持向量才对目标函数L(w,b,α)产生影响，这也是为什么该算法叫做支持向量机的原因。

在实际样本，绝大部分样本点都不是支持向量，只有少数点才是支持向量，因此支持向量机最终得到的是一个稀疏模型。

 

5. 引入松弛因子ξ

如果样本数据本身是线性不可分，如下图所示：

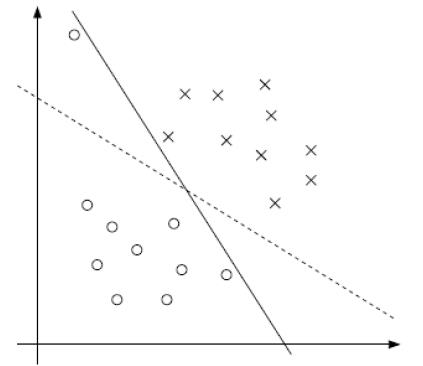
我们在原约束条件上增加松弛因子ξ（ξ>=0），让其变得线性可分，需满足：

因此目标函数也要加上松弛项：

同样地，采用拉格朗日法可以得到带约束的最优化问题：

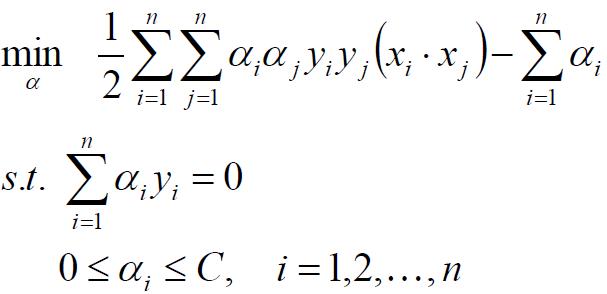
然后采用SMO算法可以求出w和b，最终得到分割超平面，在此不赘述。

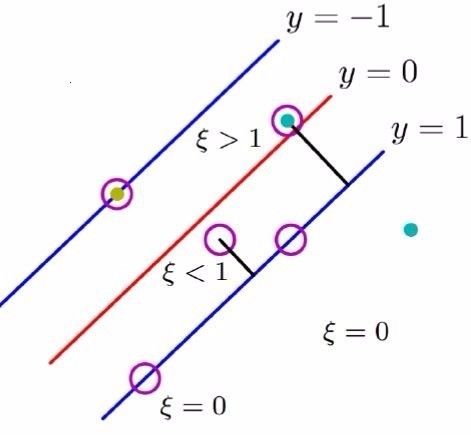
这里想解释一下目标函数中松弛因子ξ的作用。我们可以把松弛因子ξ理解为损失量：当一个正例的样本点被判定落在上边界或者上边界外时，我们认为分类正确，此时损失量ξ=0；当一个正例的样本点被判定落在上边界与分割超平面之间时，我们也认为分类正确，但是有一定的分错风险，即带有一定的损失量，只不过损失量是在可控范围的，此时损失量0<ξ<1；当一个正例的样本点被判定落在分割超平面的另外一边时，我们认为分类错误，此时损失量ξ>1。所以C Σξ可以看作损失函数，我们的目标就是使得损失函数取最小值，½||w||²则可以看作是损失函数中引入的L2正则项。

 

6. 超参数C

在待松弛因子的目标函数中，需要给定超参数C，该参数控制了SVM的训练精度。C越大，则过渡区域越窄，分割间隔越小，代表训练误差越小，可能导致过拟合；反之C越小，则过渡区域越宽，分割间隔越大，代表训练误差变大。因此增大C，可以提高训练精度；减少C可以提高泛化能力，防止过拟合。下图是给定不同的C值时的分类效果：

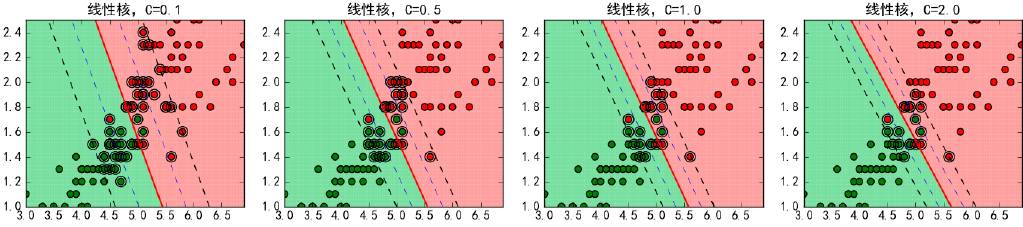
这里超参数C与分割间隔是成反比的。可以回忆一下，在岭回归与Lasso回归一节介绍正则项时，也存在一个控制缩减程度的超参数λ，λ值与约束条件大小r（即正方形或圆形的半径）是成反比的。

 

7. 核函数Kernel

核函数是计算两个向量在隐式映射到高维空间中的内积的函数。根据模式识别理论，我们可以将原始低维空间（下左图为二维空间）的样本映射到新的高维空间（下右图为三维空间），从而使得在低维空间线性不可分的样本变换为在高维空间线性可分。

但是直接映射到高维空间进行分类计算，会出现在高维空间运算时存在的“维度灾难”。那如何解决这个难题呢？这时就需要引入核函数，它可以有效解决该问题，核函数可以将高维空间的内积运算<Φ(x₁), Φ (x₂)>转化为低维空间的运算，比如（x₁* x₂）²。这样不仅可以解决在高维空间直接运算存在的“维度灾难”，大大的减少计算量；又可以利用分类算法在高维空间展现线性可分的效果，最终解决低维空间线性不可分的难题。总结一下，核函数实现了在低维空间运算，在高维空间分类。

特别说明的是，从低维空间映射到高维空间使用到的映射函数Φ是隐式函数，我们无需知道映射函数Φ的具体形式和参数。

常见的核函数有多项式核函数、高斯RBF核函数、Sigmoid核函数，其表达式依次为：

在实际应用中，往往依赖先验的领域知识或者交叉验证等方法来选择有效的核函数，如果没有先验领域知识，通常会采用使用最广泛的高斯核函数。

 

8. 实战示例

本文采用的数据集源自加州大学（圣地亚哥分校）的ChemoSignals 实验室。该实验室在2007年1月~2011年2月的连续36个月期间，通过气体发生装置的16个气体传感器采集到了13910条测量数据，每条测量数据包括128个气体相关的特征。利用这些测量值训练一个分类器，用于识别6种不同浓度的挥发性气体类型Ammonia、Acetaldehyde、Acetone、 Ethylene、Ethanol、Toluene。

该数据集提供的原始数据是dat格式，需要经过一定的预处理后再进行训练。由于该样本集数量较大，因此选择linear线性核函数。为了能寻找到最优的超参数C，我还使用了grid search方法，遍历不同C值，最终选择C=7.0时训练效果最好。下面最终模型的评估指标：

    Accuracy Score: 0.8418

    Precision: 0.8509

    Recall: 0.8498

    F1 Score: 0.843

数据集来源：http://archive.ics.uci.edu/ml/datasets/Gas+Sensor+Array+ Drift+Dataset