支持向量机算法实现

Posted 2021-04-26 gylionking

 支持向量机算法实现

一 实验目的

1、通过调用支持向量机算法的编程实现，加深对支持向量机算法的理解。

2、学习可视化图形展示方式，并对分类结果进行分析。

二 实验平台

操作系统：Windows系统或者linxu。编程软件：Python2.7或Python3.5。

三 实验内容

svm(support vector machine)是一种用来进行模式识别，模式分类的机器学习算法。svm的主要思想可以概括为二点：(1)针对线性可分情况进行分析。(2)对于线性不可分的情况，通过使用核函数，将低维线性不可分空间转化为高维线性可分的情况，然后再进行分析。

SVM算法的具体原理分成二部分，一是线性可分的情况，二是线性不可分的情况。

①线性可分情况：

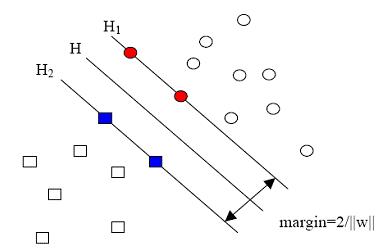
图1 线性可分示例 图2 线性可分情况

图1中间的那条线就是划分的分割线，可以用f(X)=w*x+b，w,x是向量形式，因此要找到一个目标解，即是找出分割的临界条件。图2是最佳的分类情况，即是margin最大，保证了分类的准确性。要使式（1）最大化：

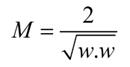
（1）

就是要使分母最小：

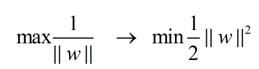
（2）

取||w||最小，其限制条件就是：

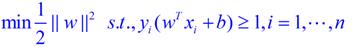
（3）

经过转换成：

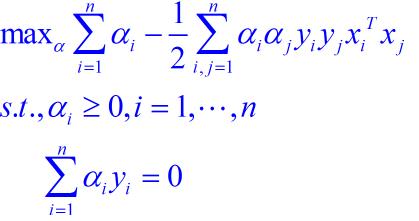
（4）

②线性不可分的情况

图3 线性不可分示例

选择不同的核函数，可以生成不同的SVM，常用的核函数有以下4种：

1. 线性核函数K(x,y)=x·y；
2. 多项式核函数K(x,y)=[(x·y)+1] d；
3. 径向基函数K(x,y)=exp(-|x-y|2/d2）
4. 二层神经网络核函数K(x,y)=tanh(a(x·y)+b）

（5）

步骤：

1、输入训练集数据。

2、提供训练集数据构建svm_problem参数。

3、设定svm_param参数中的svm类型和核函数类型。

4、通过svm_problem和svm_param构建分类模型model。

5、最后通过模型和测试数据输出预测值

参考程序mysvm.py。

实现效果;

​

实现代码：

import numpy as npy

from sklearn import svm

import matplotlib.pyplot as plt

'''加载数据1'''

x1=[]

y1=[]

for i in range(0,10):

if(i=8):

x1.append([i,i])

y1.append(0)

else:

x1.append([i,i])

y1.append(1)

x=npy.array(x1)

y=npy.array(y1)

'''创建SVM'''

#核函数

#线性核函数

linear= svm.SVC(kernel='linear').fit(x, y)

#多项式核函数

poly= svm.SVC(kernel='poly',degree=4).fit(x, y)

#径向基核函数

rbf= svm.SVC().fit(x, y)

#Sigmoid核函数

sigmoid=svm.SVC(kernel='sigmoid').fit(x, y)

#测试（预测）环节

a=1

x21,x22= npy.meshgrid(npy.arange(x[:,0].min(),x[:,0].max(),0.01),npy.arange(x[:,1].min(),x[:,1].max(),0.01))

for i in [linear,poly,rbf,sigmoid]:

rst=i.predict(npy.c_[x21.ravel(),x22.ravel()])

#plt.subplot(横向划分, 纵向划分,定位)

plt.subplot(2, 2,a)

plt.contourf(x21,x22,rst.reshape(x21.shape))

#yk设置不同颜色

#训练数据的点也绘制出来

for j in range(0,len(y1)):

if(int(y1[j])==0):

plt.plot(x[j:j+1,0],x[j:j+1,1],"yo")

else:

plt.plot(x[j:j+1,0],x[j:j+1,1],"ko")

a+=1

plt.show()

​

​

​

​

​