云通原创 | 支持向量机在私募基金投资策略分类上的应用

Posted 2021-04-26 fofpower

引入

请输入标题     bcdef

机器学习是根据样本数据寻找规律，然后再利用这些规律来预测未来的数据。目前机器学习的方法主要分为：经典参数统计估计、经验非线性方法、统计学习理论。统计学习理论在神经网络结构选择、局部极小点等问题上的应用非常广泛，支持向量机（SVM）就是基于这一理论产生的。

本文的工作是在这些分类方法的基础上，使用支持向量机进行基金策略分类准确性及有效性的验证，将会涉及基金的成立以来年化收益率、年化夏普比率、最大回撤、年化波动率等指标来刻画基金特性。如此一来，对于新的观测样本，我们就能根据基金属性，以及一系列已经分类好的历史样本，来将这个新样本分到两个不同的策略类中的某一类。

请输入标题     abcdefg

目录

⊙SVM概述

⊙  核函数

⊙  分类识别

⊙总结

01

SVM概述

首先，什么是支持向量机？简单地说支持向量机（下文简称SVM）就是用来解决分类问题的一种算法。比如我们要用一根直线将苹果和香蕉分作两堆， 这个直线与两个类最靠近的点（支持向量）的最小距离相同。

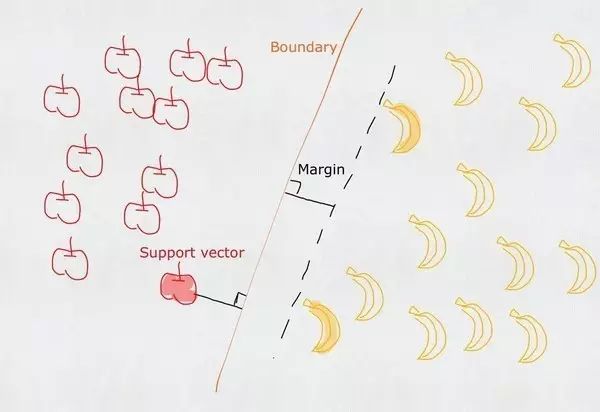
图1.用一根直线将苹果和香蕉分作两堆

但是实际问题没这么简单，考虑的问题不单单是平面距离。比如对花的两个品种分类，假设决定他们分类的有两个属性，花瓣尺寸和颜色。单独用一个属性来分类时，就像刚才分水果那样，找到尺寸这个维度的距离界限。接着设置两个值：尺寸x和颜色y，把所有的数据都丢到x-y平面上作为点，理论上如果只有这两个属性决定了两个品种，数据肯定会按两类聚集在这个二维平面上。

接着我们只要找到一条直线，把这两类划分开来，分类就很容易了，以后遇到一个数据，就丢进这个平面，看在直线的哪一边，就是哪一类。

例如：x+y-2=0这条直线，我们把数据(x，y)代入，只要认为x+y-2>0的就是A类，x+y-2<0的就是B类。

那么问题来了，如果香蕉和苹果不能用直线分开呢？比如这种：

图2.用一根曲线线将苹果和香蕉分作两堆

很简单，我们可以一掌把水果拍飞，香蕉轻飞至上层，苹果重在下层，此时再用一个平面将两类分开，俗称站在更高维度看问题，如果回到初始平面的视角上，这个分割平面将退化成一条曲线。

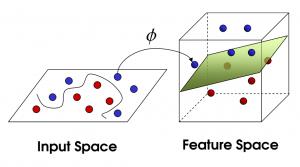
图3.在三维空间用一个平面将苹果和香蕉分作两堆

从平面上升到三维立体空间需要做一个映射，借助一个名为Kernel的工具，例如：分类的函数是个圆形x^2+y^2-4=0。这个时候令x^2=a； y^2=b，马上就变成了a+b-4=0 这种直线问题了。

这就是SVM的主要思想。

02

核函数

目前应用最多的四类核函数分别为：线性核函数、多项式核函数、高斯核函数。选择不同的核函数和参数，SVM的性能会有很大的差异，因此核函数及其参数的选择是SVM理论和应用研究中的一个重要课题。

下面列出了几个核函数的具体形式：

1）高斯核函数K(x，xi) = exp(-||x-xi||²/2·σ²)；

2）多项式核函数K(x，xi) = (x-xi+1)^d， d=1,2,…,N。

核函数方法的广泛应用，与其特点是分不开的：

1）核函数的引入避免了“维数灾难”，大大减小了计算量。而输入空间的维数n对核函数矩阵无影响，因此，核函数方法可以有效处理高维输入。

2）无需知道非线性变换函数Φ的形式和参数。

3）核函数的形式和参数的变化会隐式地改变从输入空间到特征空间的映射，进而对特征空间的性质产生影响，最终改变各种核函数方法的性能。

4）核函数方法可以和不同的算法（本文是与SVM）相结合，形成多种不同的基于核函数技术的方法，且这两部分的设计可以单独进行，并可以为不同的应用选择不同的核函数和算法。

SVM看上去是比较复杂，但是在实际应用当中还是比较简单的，因为Matlab本身就已经提供了SVM的工具箱（函数），我们直接调用就可以了，当然，大家也可以自行安装一些其他SVM的工具箱来实现。但是，和任何一个机器学习算法一样，最难的不是使用一个算法，而是真正明白我们要解决的问题。如果问题的本质需要非线性分类边界，而我们使用了线性的核函数，那结果可想而知。反过来也是一样。

03

分类识别

在私募基金投资策略分类问题上，假设我们有n只准确分类的私募基金，每一只都被标识为市场中性（0）或者相对价值（1）策略。每一只私募基金都有四个关键特征：成立以来年化收益率、年化夏普比率、最大回撤、年化波动率。

将以上问题用数学语言转化为分类问题，则我们有n个训练样本，每一个样本都是一个4维的特征向量x_i。此外，每一个训练样本都有一个已知的分类y_i（例如市场中性或者相对价值）。因此，我们有n对训练样本（x_i，y_i）。分类器将通过学习这些训练样本来优化自身的参数，得到最终的分类模型。我们使用测试样本来检查分类器的分类效果。

关于核函数的选择，我们不妨先来看一下在前文所述三种核函数下训练集的分类情况。为了方便展示，我们先选择年化收益率、年化波动率这两个特征画出二维分类图，毕竟二者是投资者最常用的收益和风险指标。首先是线性核函数：

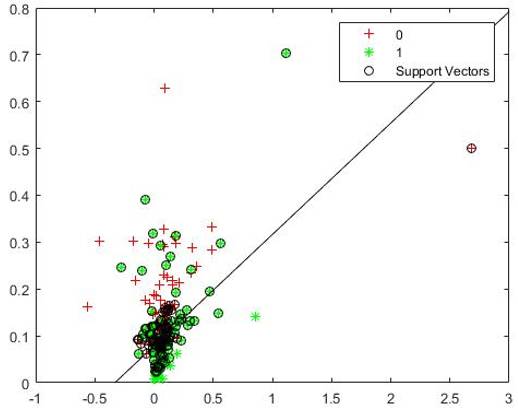
图4.用线性核函数对测试样本的分类

数据来源：私募云通CHFDB数据库

从图4可以看出，线性分类器几乎无法将两种测试样本分开，相对价值（1）策略的基金可以说是均匀地分布在这条直线两侧。

图5.用高斯核函数对测试样本的分类

数据来源：私募云通CHFDB数据库

更换核函数后，分类效果显著提升，从图5我们可以看到，市场中性（0）策略基金几乎完全被包含在圆形区域中，而绝大部分相对价值（1）策略基金在圆形区域外，只有极少数还在区域内。

图6.用多项式核函数对测试样本的分类

数据来源：私募云通CHFDB数据库

最后是多项式核函数，相比较线性核函数而言，图6的分类效果看上去要好一点，但是凭我个人的肉眼判断，还是比不上高斯。请大家细看黄色箭头所指的样本，在图6中被分为市场中性（0）而在图5被分为相对价值（1），但其本身正确分类是相对价值。当然我们不能以偏概全，关于二元分类器的效果评价方法并不少，比如ROC，AUC，Confusion Matrix等，我们准备在之后的文章中加以介绍。

04

总结

SVM的核心就是通过使用核函数（某一个给定的非线性方程），将原始的特征空间变换为更高维的特征空间。正如我们前文所说的那样，最难的不是使用这个算法，而是真正明白我们要解决的问题，到底适合怎样的核函数。下面我们来总结一下SVM的优缺点。

优点：

1）高维度：SVM可以高效的处理高维度特征空间的分类问题，在实际应用中意义深远。比如，在基金投资策略分类问题中，CHFDB库中所有不相关的指标都可以选进特征空间，特征空间的维度可以达到38维甚至更高。

2）节省内存：尽管训练样本点可能有很多，但SVM做决策时，仅仅依赖有限个样本（即支持向量），因此计算机内存仅仅需要储存这些支持向量，大大降低了内存占用率。

3）应用广泛：实际应用中的分类问题往往需要非线性的决策边界。通过灵活运用核函数，SVM可以容易的生成不同的非线性决策边界，保证它在不同问题上都可以有出色的表现。

缺点：

1）不易解释因子重要性（非常重要）：SVM取得优异的分类效果固然可喜，但投资者更愿意知道是哪些因子起了作用（解释因子的重要性）。在这方面，SVM更像是一个黑盒。当我们使用了一些复杂的非线性核函数将原始特征空间扩展到更高维的特征空间后，我们很难知道新生成的特征长什么样子。

2）非概率性：在实际分类问题中，我们希望分类器告诉我们这个样本多大的概率属于第一类，多大的概率属于第二类，这些概率有助于我们判断分类的可信程度。SVM无法直接回答这个问题，因为样本只能在超平面的某一侧。但是我们仍然可以通过计算样本点到超平面的距离来做近似的判断：样本点越远离超平面，它属于该类的可能性越高；样本点越靠近超平面，它属于该类的可能性也相应降低。

3）要求样本数大于特征数：特征数p大于样本数n会使SVM的效果大打折扣。这很好理解。因为如果没有足够的样本，就无法在特征空间中找到真正有效的支持向量，这样在面对新的待分类样本时，SVM的分类效果就会变得很差。但这一缺点很容易克服，在CHFDB数据库中找到分类确定的样本加入测试集即可。

在今后的讨论中，我们还会进一步从实战的角度介绍如何有效的使用SVM对新增的私募基金进行分类，将机器学习的过程总结成流程图加以展示，欢迎大家持续关注fofpower!

FOF EASY 是基于私募云通·中国私募证券投资基金数据库（CHFDB）开发的，旨在帮助用户结合私募市场数据了解自有产品的业绩和风险情况，并以辅助机构投资人进行产品分析、投顾挖掘、组合产品设计和动态跟踪产品，及时提示风险，发现问题。

免责声明

本文中所提及的基金产品及投顾公司仅为展示说明功能，不构成任何投资参考意见，亦不构成财务、法律、税务、投资咨询意见或其他意见，对任何因直接或间接使用本文所涉及的信息和内容或者据此进行投资所造成的一切后果或损失，私募云通不承担任何法律责任。

私募云通

提供私募基金数据服务，包括通用数据和定制化数据服务；提供私募基金全市场分析、投资策略分析、基金产品业绩归因、投顾尽职调查等服务。

欲了解更多私募云通产品，请登录。

FOF EASY 注册/登陆网址：

公司邮箱：[e-mail]  

联系人：陈经理  134-7278-2097