支持向量机+易中天品三国

Posted 2021-04-26 AI从零开始

学习就是一种另类的旅行

唯物论，唯心论是两种对立的世界观。人们的认识总是二元对立的，有没有人考虑过世界是高元对立的呢？且先不说这个，旅行是物质的实践活动，这是对物质世界的探索，是一种对最原始的的美的一种追求；同样，读书学习是精神的实践活动，这是对精神世界的探索，和旅行一样，也是一种对最原始的美的一种追求。所以建议大家，常旅行，多读书！

江东流

摘要

第一部分：

支持向量机（SVM）的学习

第二部分：

易中天品三国笔记分享

支持向量机

Support Vector Machine

原理介绍

在机器学习中，支持向量机是一种最有影响力的监督学习模型之一。可以分析数据，识别模式，在小样本、非线性和高维模式识别中表现较好。用于分类和回归分析，本文主要介绍分类任务。

高维优势：

SVM的最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了高维变量引起的灾害。（如果没有基础，看不懂，就先看下边的原理哈）

相比较神经网络：

如果说神经网络方法是对样本的所有因子加权的话，SVM方法是对只占样本集少数的支持向量样本“加权”(支持向量样本下文有解释)。当预报因子与预报对象间蕴涵的复杂非线性关系尚不清楚时，基于关键样本的方法可能优于基于因子的“加权”。少数支持向量决定了最终结果，这不但可以抓住关键样本、“剔除”大量冗余样本，而且注定了该方法不但算法简单，而且具有较好的“鲁棒”性。

非线性可分：

使用核映射的非线性模型。对于线性可分的训练样本，存在一个超平面能将训练样本正确分类。在实际任务中，原始输入样本空间并不一定线性可分，但是通过对原始样本进行核映射的非线性变换后的特征空间是可以分的，可以说特征空间线性可分的，也可以说是原始输入样本空间是非线性可分的。如下图所示

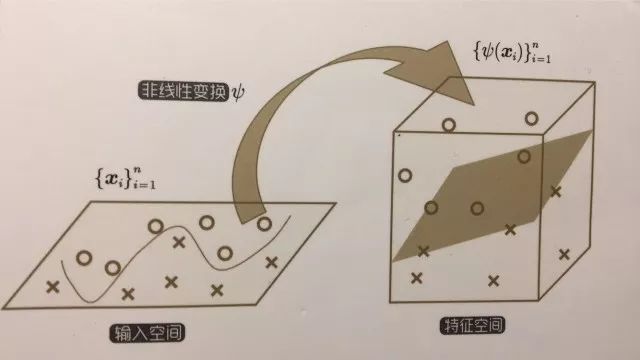
原理说明：

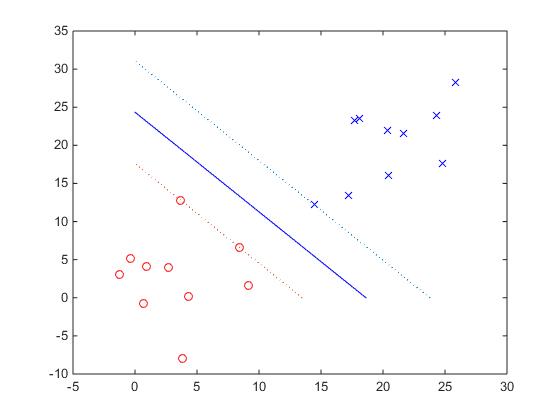
对于一个线性可分的二分类问题，我们想找一个超平面，该超平面可以将样本数据分为两类，如果线性可分，很明显有无数个超平面可以做到这一点，而支持向量机是寻找间隔最大的那个超平面，且到两类最近的样本的距离相等。 思想就是这么简单，我们再来分析一下这种分类方法为什么叫支持向量机，首先，这种分类方法只与分类器距离最近的两异类样本有关，与除去这些样本的其他样本无关。注：每个样本对应于一个特征向量，所以叫支持向量机，“机”表示机器学习算法，是支持到超平面距离最近的样本（特征向量）的机器学习算法。支持向量机二维数据分类如下图所示

超平面：

我们还记得中学学的直线的一般方程吧，Ax+By+C=0，将x看做x1，将y看做x2，就是一般意义上的直线了（这里说的很详细，怕基础较差的朋友看不懂啊），直线可以看做是一维的平面，如果存在多个维度x3，x4.......这样的图像就是超平面！

间隔最大分类：

最大间隔就是支持向量机的目标函数，最大化问题转化成最小化问题来求解，约束条件上图中已经给出，这就是支持向量机的基本型。

支持向量机的求解：

显然，这是一个凸二次规划问题，可直接求解，也可以使用拉格朗日对偶问题等方法来解，本文不再列出具体解法，可参考周志华的《机器学习》。

核映射：

这是支持向量机的一个重要特点，在上文非线性可分中已经讲到了，输入样本空间线性不可分的时候，经非线性运算，转化的特征空间，对于有限维原始空间来说这种方法是可分的。例如“异或”问题，二维线性不可分，转化的另外一个更高维空间就可以分了。

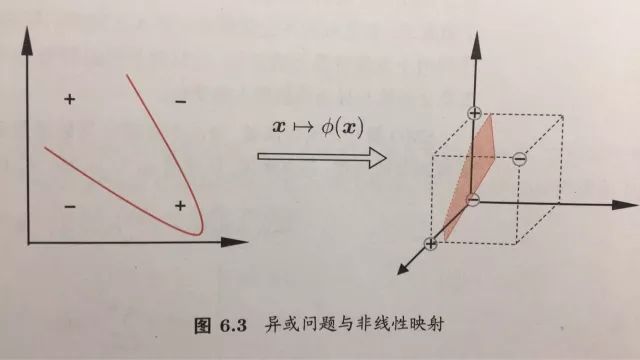
周志华的书中有这么一句“幸运的是，如果原始空间是有限维，即属性数有限，那么一定存在高维特征空间使样本可分”这句话当然没问题，我这里进一步挖掘一下哈，对于上边的异或问题可得

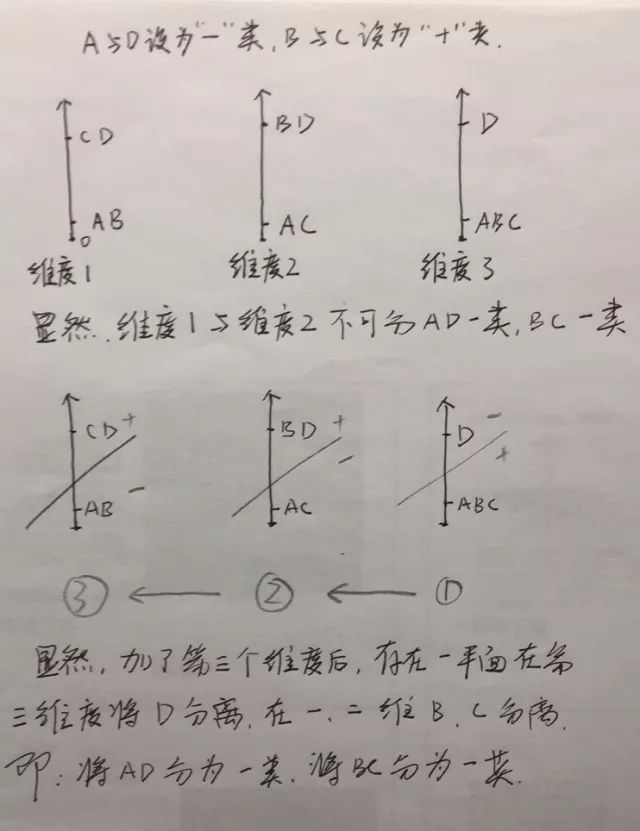
误区：只要维度足够高，异或问题就可分。

这是不正确的，一个简单的例子，高纬度重复维度一或者维度二的分布就不可分！

由于在算法求解的时候，只涉及到输入样本空间x间的内积运算，在特征空间也只涉及到样本映射后的数据间的内积运算，这种特征空间维度可能很高，计算也太大，所以可以用适当的核函数来表示，简化运算。那么这种从输入样本空间到特征空间的变换就可以用核映射来表示了。也正是这种机制，在不知道特征映射的形式时，就不知道什么样的核函数是合适的，核函数也仅是隐式的形式定义了特征空间，这就使得“核函数选择”成为支持向量机的最大变数，核函数选择不合适，就会导致分类性能不佳。

MATLAB程序代码分析：

function u = svm( X,Y )%子函数

%SVM 转化为凸二次规划

%列出凸二次规划的参数，然后带入quadprog函数中即可求解

    [K,N] = size(X);

    u0= rand(K+1,1); 

    A = - repmat(Y,1,K+1).*[ones(N,1) X'];

    b = -ones(N,1);

    H = eye(K);

    H = [zeros(1,K);H];

    H = [zeros(K+1,1) H];

    p = zeros(K+1,1);

    lb = -10*ones(K+1,1);

    rb = 10*ones(K+1,1);

    options = optimset;    % Options是用来控制算法的选项参数的向量

    options.LargeScale = 'off';

    options.Display = 'off';

    options.Algorithm = 'active-set';

    [u,val] = quadprog(H,p,A,b,[],[],lb,rb,u0,options)

end

    function test_svm()%主函数

    close all;

    %定义样本点数据

    t1  = 5+4*randn(2,10);

    t2 = 20+4*randn(2,10);

    X = [t1 t2];

    Y = [ones(10,1) ; -ones(10,1)];

    %绘制图形

    plot(t1(1,:),t1(2,:),'ro');

    hold on;

    plot(t2(1,:),t2(2,:),'bx');

    u = svm(X,Y)%u(1)=b,u(2)=x1,u(3)=x2;

    x = [-u(1)/u(2) , 0]

    y = [0 , -u(1)/u(3)]

    plot(x,y,'b');%绘制超平面

    x1 = [-(u(1)+1)/u(2) , 0]

    y1 = [0 , -(u(1)+1)/u(3)]

    plot(x1,y1,':');%绘制w'x+b=1 超平面

    x2 = [-(u(1)-1)/u(2) , 0]

    y2 = [0 , -(u(1)-1)/u(3)]

    plot(x2,y2,':');%绘制w'x+b=-1 超平面

    end

运行结果：

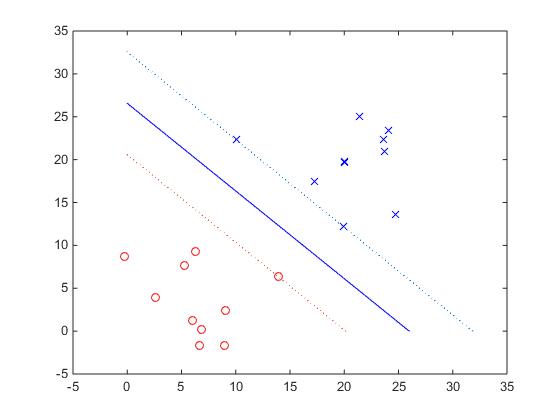
由此可见，SVM分类效果较好。有的时候为了防止过拟合，也常用软间隔SVM，具体内容此处不多涉及，感兴趣的朋友可以自行学习，然后与我一起探讨~~~

哦对了，给大家出道小题目哈，看看大家学的如何吧：

支持向量机就先给大家介绍到这里吧，代码我都发到咱们群里了，下面是本文的一些参靠文献。有什么疑问，欢迎大家留言和交流~~~

参考文献

（http://blog.sina.com.cn/s/blog_7798183d0102v2lo.html#cmt_567F3860-7F000001-668E24B8-86B-8A0）

2、支持向量机SVM 原理、推导与Matlab实现http://blog.csdn.net/TaiJi1985/article/details/75087742

3、周志华《机器学习》

4、衫山将《图解机器学习》

易中天品三国

部分笔记分享

恍惚之间，一个学期又过去了，研一的上学期结束了，这学期小编看了一部大型历史演播类节目《易中天品三国》，一般是很少看电视局之类的节目的，细细回想大四之前十年左右，好像也就看过一部电视剧《北平无战事》，看的电影也不多，直到大四保研之后，才疯狂的恶补了一下。

三国是一个风云变幻，沧海横流，英雄辈出，令人神往的时代。小编的英雄心啊，对这种乱世英雄很是羡慕。不知道大家如何看待这部局，看过的朋友，我想问一下这部剧是什么吸引了你？我喜欢这部剧是因为敬佩里边的英雄，将之作为学习的对像。下边是我从中学到的部分笔记，供大家享用~~~

1、定国之术，在于强兵足食。

2、天下大乱，首倡义兵，屯田备战。（正义之师，顺天应命）

3、夫济大事，必以人为本。（刘备，以人为本最早出处）

4、携天子以令诸侯。（天时）

5、团结大多数，打击一小撮，首恶必办，胁从不问。

6、理想主义者共同特征，抓住每一点机会。（小机会，大机缘）

7、宝刀赠烈士，货卖与识家。把真实的感情作为一种政治手段表演出来。（高明）

8、做人情的诀窍，是千万不要让对方觉得你在做人情。（曹操对待汉献帝）

9、耗子腰里别了杆枪，起了打猫的心。（哈哈）

10、打败了检讨自己，打胜了感谢别人。有成绩归功别人，有错误责备自己。（真英雄！）

11、中庸之精髓，常规与权宜。

12、每个人都有毛病，这不重要，重要的是知人善任。

帅才

当今之世，缺乏的不是将才，是帅才。将才，精通一门技术，掌握某个领域的精髓即可。而帅才，则需要纵横古今中外的视野，需要顺天应命的情怀，需要时可以做将才的格局。所以，在此建议大家，要有理想，有视野，有情怀，有格局！

与其相忘江湖，不如青梅煮酒

在这个寒冷的时节里

因为有你的关注

而变得温暖