量子支持向量机QSVM

Posted 2021-04-26 量子机器学习

【写在前面的话】关于前期文章的集合，可以参见。

前期文章中的算法解读，都是针对一些经典的简单的运算，比如求解线性方程，或者奇异值阈值算子。这些运算可作为子程序用于机器学习算法中。

接下来的文章，咱们就针对更具体的量子机器学习算法进行解读。今天，咱们先来看一看，量子支持向量机QSVM。

Preliminaries

SVM：Support Vector Machine, 支持向量机；

QSVM： Quantum Support Vector Machine, 量子支持向量机。

参考文献：

[1] Patrick Rebentrost, Masoud Mohseni, and Seth Lloyd. Quantum Support Vector Machine for Big Data Classification, Physical Review Letters, 

113, 130503 (2014). 

[2] 李航. 统计学习方法[M]. 清华大学出版社, 2012.

本期大纲

我们从以下几点进行展开：

1. SVM概述

2. QSVM解决的问题

3. QSVM算法

SVM概述

我们从机器学习中简单的分类开始。机器学习算法可以简单的分为两类：非监督学习和监督学习，两者的主要区别在于前者事先不知道样本的标签，而后者事先已经知道样本的标签。同样，算法可以用于求解回归问题（输出的是连续数据类型），也可以用于求解分类问题（输出的数据类型是离散数据）。一个简单的举例如图1所示。其中，我们讨论的SVM属于用于分类问题的监督学习算法。

Note: SVM算法也可用于回归问题。

图1 Machine learning algorithms (sample)

我们简单的介绍下SVM。SVM利用了少数的支持向量，通过一个分类超平面将数据分为两类，使这两类之间的间隔最大化，因此它也被成为最大间隔分类器。如图2所示，超平面将红绿两类元素进行分类，使两类之间的举例m达到最大，处于虚线上的点称为支持向量。

这里重点记录两个变量，法向量w和偏移量b，它们是决定这个超平面的参数。

图2 Support Vector Machine

一个支持向量机通过线性可分器实现。目标是寻找到一个超平面能够最好的区分两类数据，并且提供了一个决策边界供后续的分类任务。一个简单的例子是一个一维的线性数据，在点x的两边的数据分别属于类1和类2。在多维的情况下，一个超平面作为边界，在超平面一侧的数据属于一类，在超平面另一侧的数据属于另一类。图中给出的是一个二维的情况。对于线性不可分的情况，可以通过映射实现低维度到高维度的转换，使其变成线性可分。

有关SVM的更深入学习可以参考李航编著的《统计学习方法》[2]。

QSVM解决的问题

虽然SVM只利用了少量的支持向量，但在计算上还是遍历了所有的样本和所有的特性，因此时间复杂度是特征数量N以及样本数量M的多项式级。当样本数量很大，比如达到TB（2^40）和PB（2^50）级，计算量是相当大的。

在大数据的背景下，量子算法能够提供一个指数级的加速，就像经典中处理1TB的数量，在量子中只要40个量子比特的数量级就可以了。

在2014年MIT和GOOGLE研究所联合发表在PRL的Quantum Support Vector Machine for Big Data Classification这篇文章中，介绍了QSVM的实现方法。

QSVM算法

图3是小编自己总结的文中的一个脉络，也许和作者原来的思想不同，仅供参考。这篇文章小编总结是通过两个量子方法解决了SVM中涉及的两个参数的计算复杂度问题。

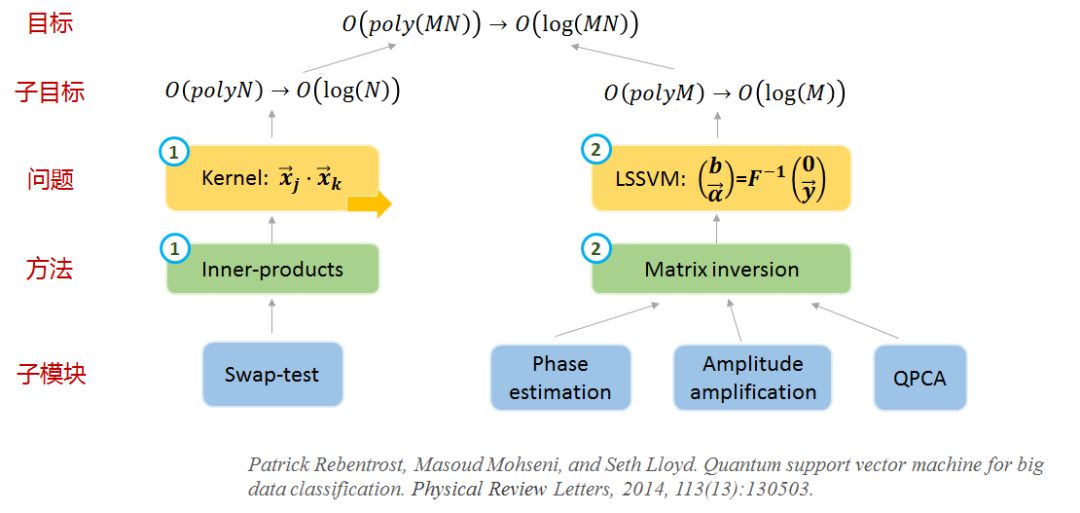
图3 Outline of QSVM

接下来介绍这两个问题及相应的量子求解算法。

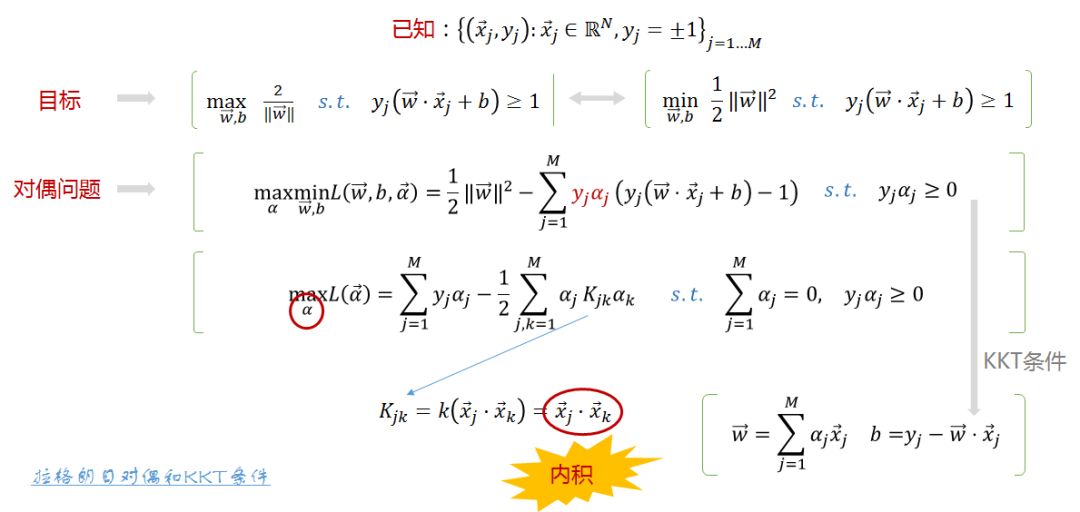
图4 问题1

首先是第一个问题。原始的SVM算法是约束最优化问题。

在求解原始的SVM算法时，会将原始问题中对前面提到的参数w和b的求解，通过拉格朗日对偶及KKT条件转换为对拉格朗日乘子alpha的求解，最终通过带入alpha得到原始问题的解w和b（关于KKT条件可参考《统计学习方法》P227）。

在求解alpha时，会涉及到核函数，也就是样本之间的内积操作。经典算法复杂度是O(N)，量子的swap test方法可以达到O(logN)，关于该算法具体可参见前期文章。

求得内积后就是求解alpha，解alpha是一个二次规划的问题，这篇文章并没有对原始SVM进行分析，而是对最小二乘支持向量机LSSVM的求解进行了分析。我们接下来看问题2。

图5 问题2

LSSVM通过引入松弛变量e_j，将原来SVM的不等式约束转换为等式约束y_j^2=1，大大方便了拉格朗日参数alpha的求解，将原来的QP（Quadratic Programming二次规划）问题转换为求解线性方程组的问题。量子算法在求解线性方程组时能够达到指数级的加速，因此可以用于对LSSVM的求解。量子求解线性方程组的算法请参见前期，算法的完整链接可参见。

Note: 等式中的参数γ决定了训练错误和SVM目标之间的相关权重（determines the relative weight of the training error and the SVM objective）。

QSVM 算法：训练

我们通过两张图来简单了解下QSVM算法训练过程的流程。图6为文字版，图7为线路版。

图6 QSVM算法：训练

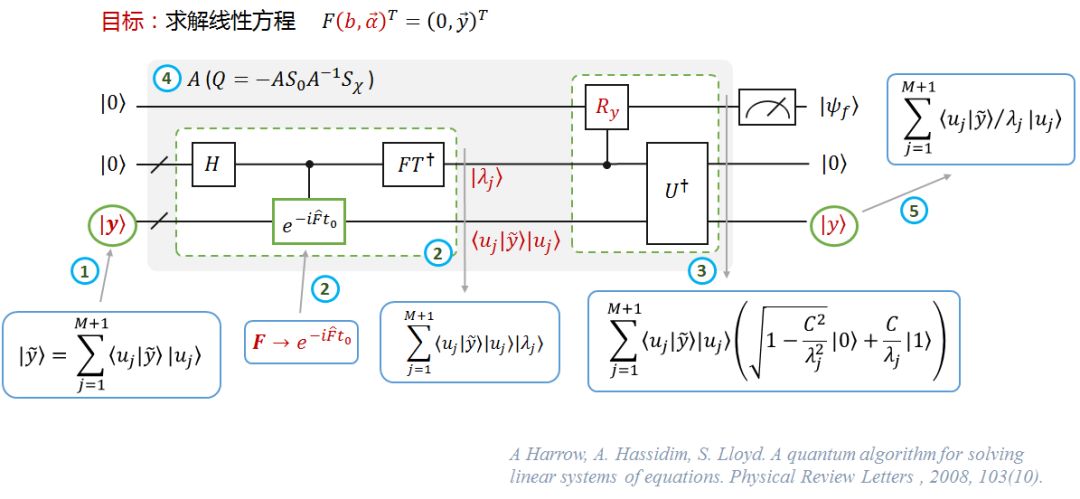
图7 QSVM算法：训练

图7的线路与HHL算法的相似，这里不再赘述。具体参见。

对于QSVM算法中，最重要的一个部分是矩阵F的模拟，所以文中详细给出了了F的模拟方法。主要分三个层次。

【1】模拟e^(-iF ̂Δt)：对于算法第二步的输入，模拟 e^(-iF ̂Δt)的核心是模拟K∕trK。

【2】模拟K ̂=K/trK：这一步核心操作可以通过约化密度算子来实现，也就是通过对密度算子求偏迹运算得到。

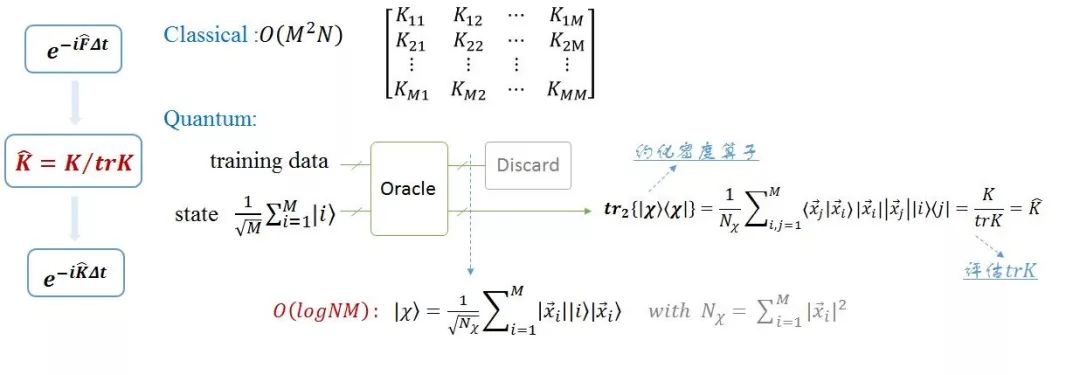
【3】模拟e^(-iK ̂Δt)：如果K ̂是稀疏的，可以有效的模拟。在K ̂为非稀疏矩阵时，QPCA这篇论文中提供了一种对非稀疏对称或厄密矩阵的有效模拟方法。

通过这几步的拆分最终可以实现 e^(-iF ̂Δt)的有效模拟。关于图中公式的推导，请参见文末附录。

QSVM算法：分类

图8简单的总结了关于用于分类的QSVM算法。

图8 QSVM算法：分类

下期预告

本期先介绍这么多喽。小编在理解上也可能会存在错误，希望大家多多指正。下期将介绍QSVM算法用于非线性SVM及其误差分析。

此外，有读者留言说希望介绍量子强化学习的专栏，小编目前对这个方向不太了解，希望对这个方向有认识的童鞋来约稿呀~

新的学期，一起分享，一起进步~

附录

QSVM[1]中公式3的推导。

关于这个公式，小编曾苦苦推导了两天，分享给大家。

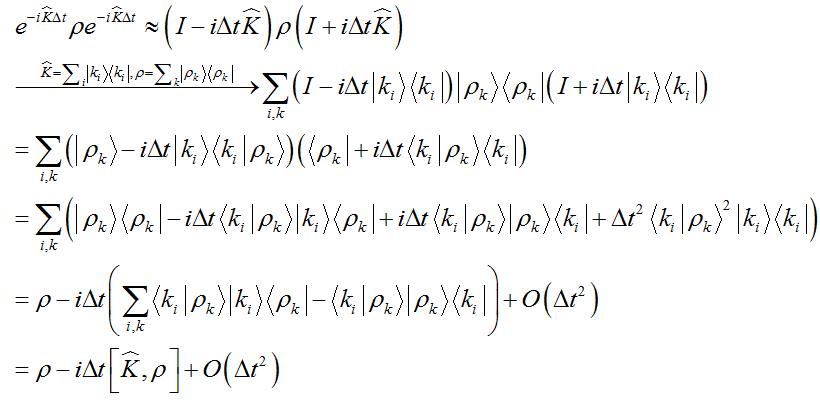
如果你希望在这个领域中深造，

加群请备注学校-专业-姓名，谢谢！