专栏机器学习-SVM支持向量机-Demo
Posted ABC技术研习社
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了专栏机器学习-SVM支持向量机-Demo相关的知识,希望对你有一定的参考价值。
就目前而言,都没有一本书对于SVM有个看的过去的科普。所以这里来讲一讲吧。
支持向量基思路与神经网络大相径庭
相比较而言SVM植根于凸优化理论,具有良好的最优化性,而对于神经网络而言并非是一个严谨的凸优化过程。
但是相比较而言SVM在算法上理解起来比神经网络更加难以理解,这其中设计拉格朗日函数、对偶问题,可能更加难以理解的问题是内积核,这个是由前面两个概念所推演而出的。从另一方面而言SVM是不反直觉的。所以这里推荐一本介绍比较详细的书《神经网络与机器学习》第六章。
最优化问题
支持向量机需要最大化向量距离,同时满足支持向量约束:
其中
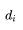 是分类标签(-1, 1),
是分类标签(-1, 1),
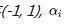 为拉格朗日乘子,这是一个稀疏的,只有支持向量不为0。两个分类目的在于两个分类边缘最大化。
为拉格朗日乘子,这是一个稀疏的,只有支持向量不为0。两个分类目的在于两个分类边缘最大化。
对偶问题为, 最大化目标函数:
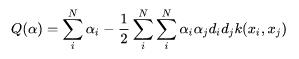
这个k就称为内积核。
可能我们最熟悉的一张图是这个
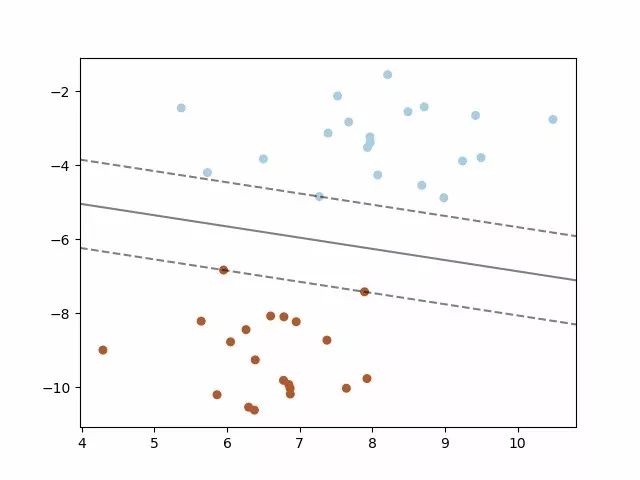
上面虚线所经过的点就是支持向量,其是对于最大化对偶函数求解过程中,alpha不为0的就为支持向量。具体公式推演请参阅《神经网络与机器学习》第六章。
这张图对于我们理解问题没有任何帮助,反而会限制我们的思维,比如遇到这种情况:
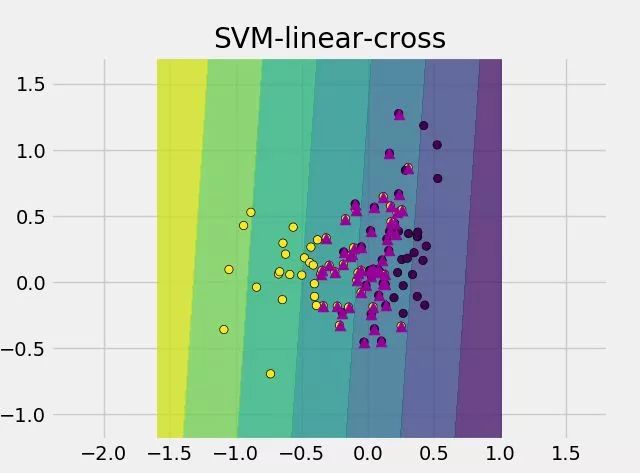
三角形的点所对应的就是支持向量,此时支持向量如何理解呢?
我们来看下决策曲面:
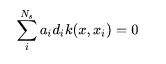
 是支持向量个数,可以看的所谓支持向量就是为了形成决策曲面。而训练过程就是挑选出合适的支持向量以得到超曲面。
是支持向量个数,可以看的所谓支持向量就是为了形成决策曲面。而训练过程就是挑选出合适的支持向量以得到超曲面。
同时可以看到SVM实际于更接近与曲线拟合问题,这种分类的复杂性隐藏于支持向量与核函数之中。而非神经网络所类似将复杂性显式的置于权值之中。因此对于分类问题其效果要比等效单层神经网络的朴素贝叶斯算法更优秀。同时有限项多项式自带抗过拟合效果(也就是粗枝大叶的分类)
来换个rbf核函数:
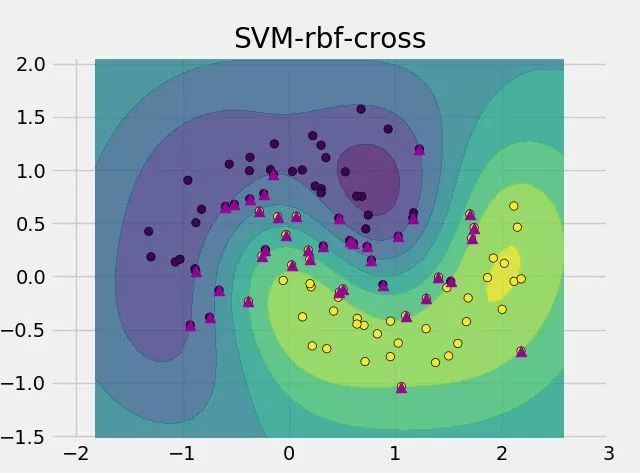


以上是关于专栏机器学习-SVM支持向量机-Demo的主要内容,如果未能解决你的问题,请参考以下文章