AI | 机器学习故事汇-支持向量机 (SVM)
Posted 海量数据学院
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AI | 机器学习故事汇-支持向量机 (SVM)相关的知识,希望对你有一定的参考价值。
作者简介:唐宇迪,海量数据学院执行院长,计算机博士,深度学习领域的一线实战专家,专注于机器学习、计算机视觉与图像识别领域,曾参与多个国家级计算机视觉项目,并在图像识别领域有着丰富经验,实现过包括人脸识别、物体识别、关键点检测等多种应用的最新算法。
【目标】本系列算法讲解旨在用最简单易懂的故事情节帮助大家掌握晦涩无趣的机器学习,适合对数学很头疼的同学们,小板凳走起!
对于一个分类任务而言,最主要的目标就是能分得开,但是对于上图当中的两类数据点来说,我可以找到三条线把它们都完全分得开,其实可以找到无数条的!那么问题也随之而来了,到底选谁呢?第二点,如果数据本身就很复杂,我们的这个线性分类还够用吗?第三点,这么强大的一个算法,它的计算复杂度怎么样呢?这些就是我们现在面临的问题,准备逐一攻克吧!
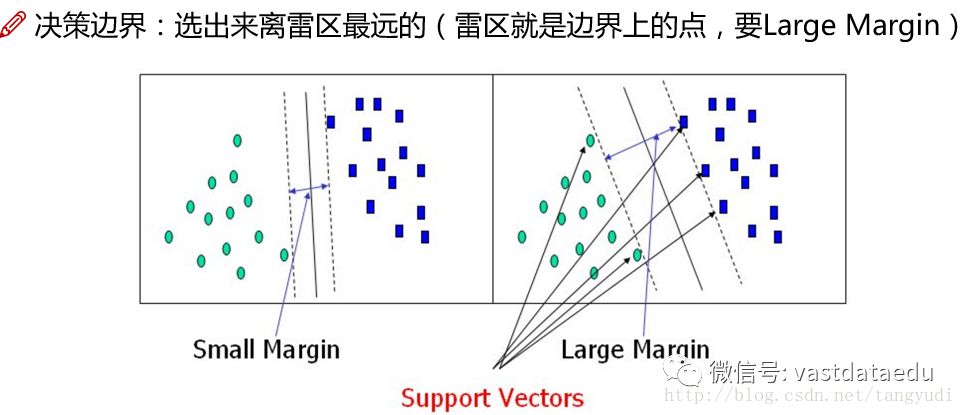
以上两张图,左边的决策区域小一些,右边的大一些。但是这两张图都完成了一个任务,完全把数据点切分开了。这个可以这样比喻,假设左右两边的数据点是交战双方的雷区,想想战狼2最后是不是从两个交战区域冲出来了?

两边都是雷区,我们现在要开辟出来一条隔离带,既不能碰到任何一个雷,还得让我们的大部分安全通过,那这条隔离带你说左边的好还是右边的好呢?必然是右边的吧,因为更胖一些,这样我们的部分更安全,说白了我们要的决策边界泛化能力应该更强一些的。
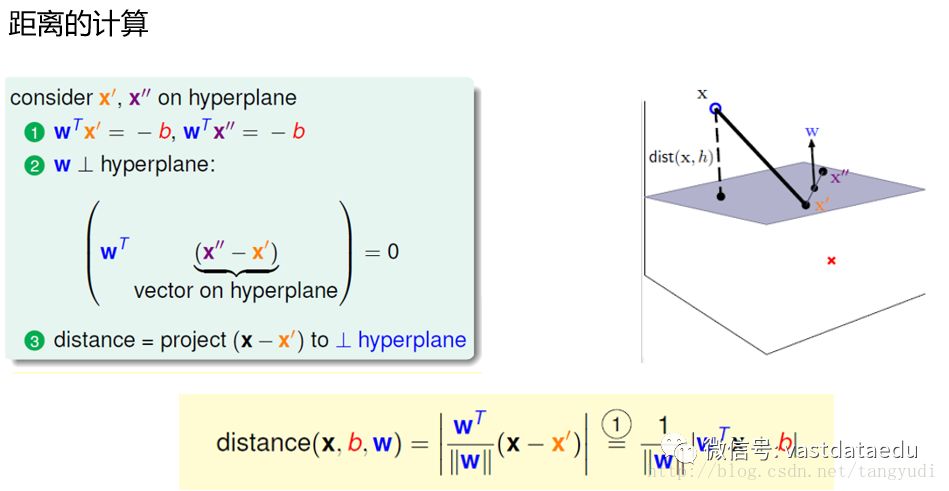
既然说到雷了,最起码的一个要求就是不能碰到它。那么我们来想,你要是碰到雷应该先碰哪个呢?离你隔离带最近的那个吧?那这里我们就得说说距离这个问题了,它决定了雷距离咱们隔离带有多远。
假设我们的隔离带就是这个平面,有一个雷X,那么现在咱们来算一下这个雷到我平面的距离有多远。直接算感觉好像有点难,咱们来转换一下,这里假定平面上有两个点X'和X'',如果我知道X到X'的距离,然后把这个距离投影到我的垂线方向,这样就间接的计算出雷X到平面的距离了。平面的垂线方向又恰好是它的法向量,只要求出它的单位向量就可以啦。问题迎刃而解,这样就有了一个雷到隔离带的距离了。

接下来对我的数据集进行如下定义,支持向量机是一个经典的二分类问题,在这里我们认为如果说一个点就是一个正例,那么对应的标签值就是+1,如果一个点是负例,那么对应的标签值就是-1。对应于我的决策方程,就可以做这样的定义:如果预测值Y(x)>0,它是一个正例;如果 Y(x)<0,它是一个负例。两个式子看起来有点多,整合一下吧,既然>0的时候标签值为+1,<0的时候标签值为-1。那么它们的乘积就必然是恒大于0的啦!

下面咱们来看一下我们要优化的目标是什么呢?我现在要找最好的一个隔离带(也就是决策方程,说白了就是w和b),这个隔离带要能够尽可能的安全,所以就要使得离它最近的那个雷(先会碰到最近的)越远越好。只要大家能理解这句话,支持向量机也就差不多有个概念了。在看点到决策边界的距离,原始的式子中有个绝对值,现在我们展开也可以,因为y*y(x)恒正。

来看我们要优化的目标,先求最小,之后又求最大,是什么意思呢?想想咱们的隔离带,就是先求最近的雷,然后让这个雷滚的越远越好。这就是我们最小和最大的意思。但是现在这个式子看起来有点复杂,能不能简化一下呢?我们认为y(x)恒大于0,现在咱们把这个条件放的宽松一些,可以通过放缩变换让y(x)>=1,这样问题就简单了。既然要求y*y(x)的最小值,现在最小值就是1,这样这个式子能化简掉了。

下面只剩下求解一个最大值啦。但是我们的常规套路是把一个最大值问题转换成一个最小值问题,那可以直接求它倒数的最小值。这个带有约束条件的极值问题该怎么求呢?自然想到了一个神器:拉格朗日乘子法。这个概念如果没接触过,可以这样理解:现在我的目标是找到最合适的W和B,但是这样还带约束的条件看起来比较难,所以我们想把这样一个问题转换成一个求解容易些的中间值问题,这个中间值能够和W还有B扯上关系,这样求出来了中间值就能找出来W和B了。

这个式子就是我们标准的拉格朗日乘子法,感兴趣可以翻翻咱们的高数书来回顾下。

这里我们利用了对偶条件,看起来就是最大最小调换了一下。其实这是一个证明,可以参考下拉格朗日KKT条件。接下来要先求解什么样的w和b能够使得当前的L式子的值最小。这个我们自然想到了直接求偏导,也就是分别对w和b求偏导,然后得到了上述式子。 
将得到的解带回到原式当中,相当于把w和b就约分掉了,那么我们现在要求解的就是什么样的a值,能够使得这个式子最大。 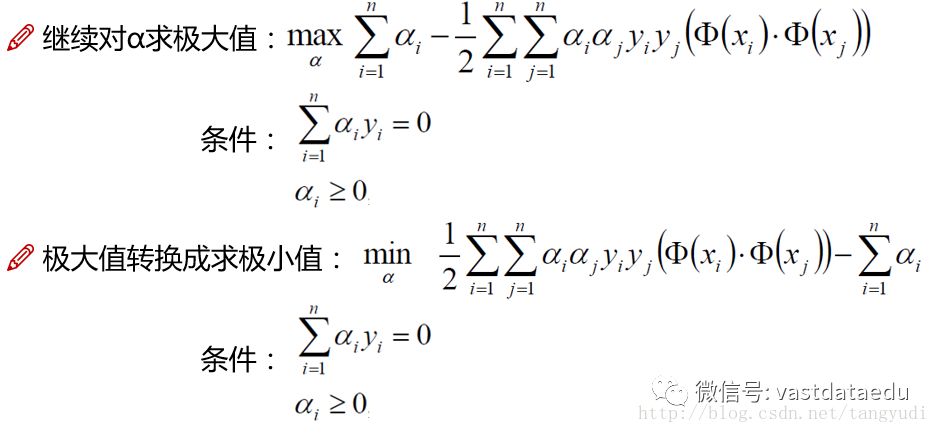
对要求的极大值式子同样加上了相反数变换成了求极小值的问题,到这里已经接近我们最终的答案啦~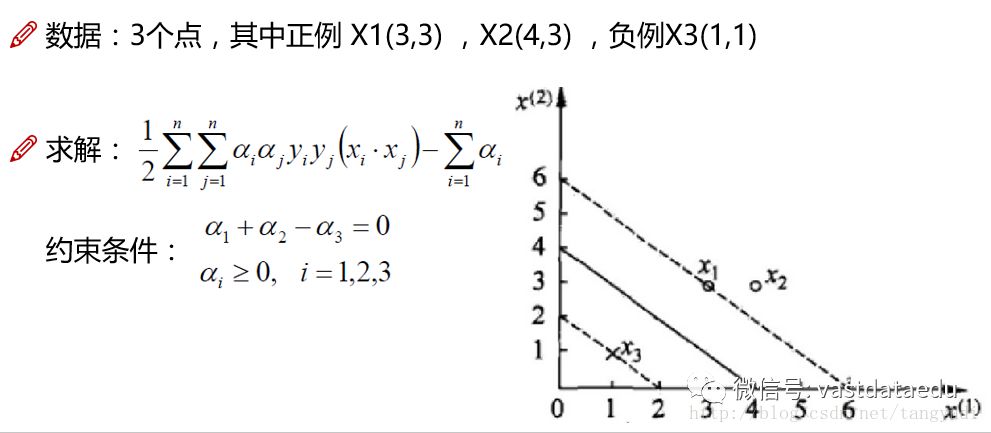
来看一个小例子吧,这个只是举例来说SVM怎么求解,真正的求解方式请参考SMO算法。这里我们有三个数据点,2个正例、1个负例,通过它们要得到最好的决策方程。在约束条件中,就要把之前所考虑的条件都带上,拉格朗日乘子法也有自身的约束条件,就是所有的a值必须都大于0。
对于这样的式子,将我们的数据全部带入就好了,注意一点,这个x之间求的是内积! 
在求极值的过程中,我们直接对a1和a2求偏导得到了结果,但是发现结果却不满足我们的约束条件,这怎么办呢?既然极值点不满足,我们只能在边界上来寻找了。 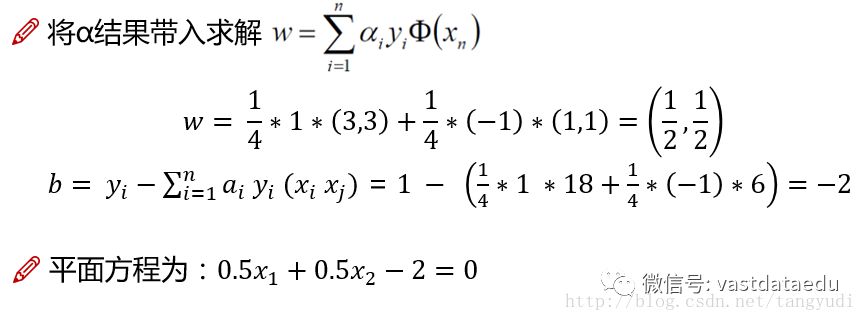
在边界上我们求出来所有的a值,这样就完成了求解的任务!因为我们知道a和w之间的关系,再继续求解就能够算出来w和b,到此我们就求解出来了,这个问题的解有了决策边界。
回过头来想一想,对于a值来说,有些算出来是一个数,有些算出来就是0,咱们的a2就是0,回到那3个点的图中看一下,会发现2号样本点是非边界上的点。那咱们来想它的a值等于0,最终的w在计算的时候就跟它无关了,那么在这里我们得出了一个非常重要的结论,支持向量机是由边界上的点所支撑起来的(因为边界上的点的a值不为0,非边界上的点的a值为0),那么我们就把边界上的点叫做支持向量。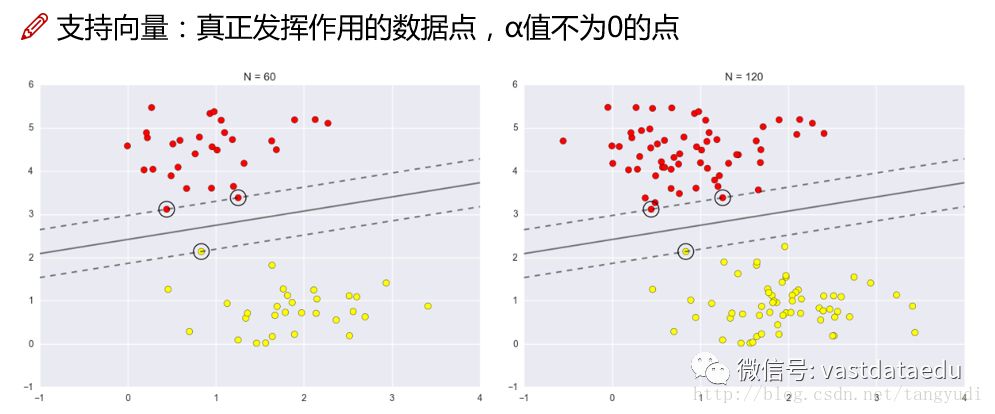
这里做了这样一个实验,保证边界上的点不变,然后在数据集中增加数据,发现决策边界没有发生变化。左边是60个数据,右边是120个的,只要支持向量没变,边界就不会变,这就是支持向量机,因为再加的点a值都为0。

新问题又来啦!在这里我们发现了在构建决策边界的过程中,如果某一个点比较特(离群点),我们的边界会为了满足它而把隔离带做的很小,这该怎么办呢?让我们的决策边界要求放低一些吧。 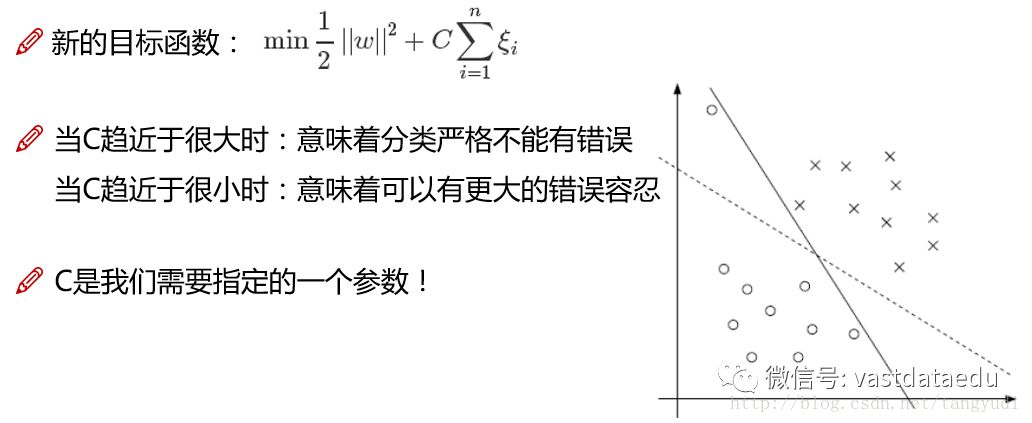
由于之前的要求太严格了,在这里我们指定了一个新的东西叫做松弛因子,在目标函数中把它考虑进来了,什么意思呢?引入了参数C相当于松弛因子让咱们决策边界放松的大小。如果C很大,那我们还想让目标函数很小,松弛因子就得很小。如果C很小呢?那么松弛因子稍微大一些也没关系。
又一个问题来啦,现在我的数据复杂起来了,在低维中很难进行区分,这该怎么办呢?一个最简单的想法就是把数据映射到高维空间,这样特征信息就更多了,决策边界就更容易建立出来。
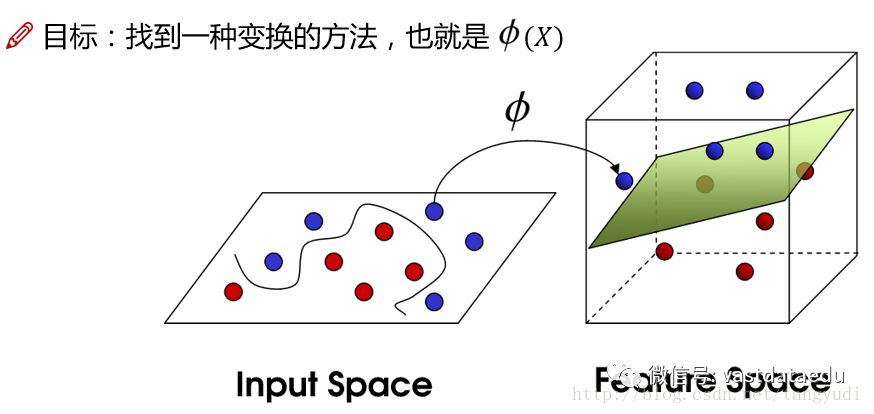
这里我们要做的就是找到一种变换的方法,将数据的特征进行高维的映射。但是问题也来了,这样的计算复杂度也上来了。其实是这个SVM在数学上有这样一个巧合,我们可以把高维特征的内积在低维当中直接计算好,然后做映射也是一样,恰好解决计算的问题!
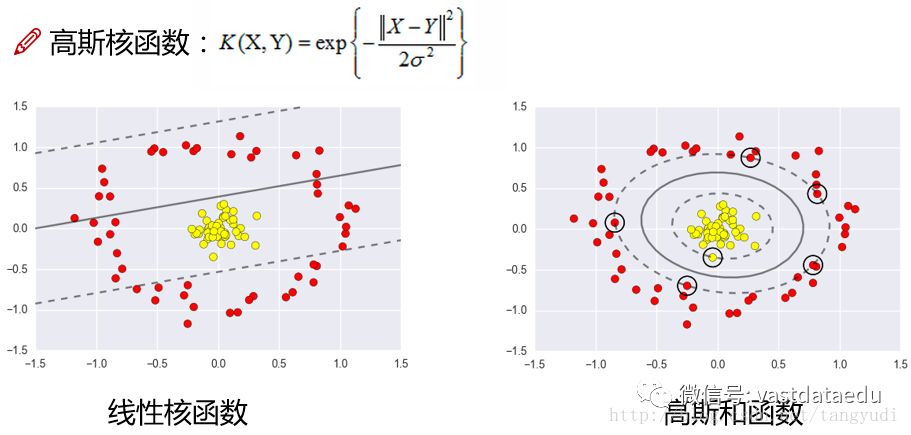
这个就是线性的和经过核函数特征变换后的结果。这些就是咱们支持向量机的推导啦。
海量数据学院开课啦
Python 机器学习
培训时间:
2018 年 4 月 20-22 日
培训地点:
上海(支持远程听课)
面向人群:
机器学习/数据挖掘工程师、转型 AI 的开发工程师
培训讲师:
唐老师,海量数据学院执行院长,计算机博士,深度学习领域的一线实战专家,专注于机器学习、计算机视觉与图像识别领域,曾参与多个国家级计算机视觉项目,并在图像识别领域有着丰富经验,实现过包括人脸识别、物体识别、关键点检测等多种应用的最新算法。
课程简介:
使用数据领域最主流语言 Python 及其分析与建模库作为核心武器。对于机器学习经典算法给出完整的原理推导并基于实例进行讲解,基于案例演示如何应用机器学习算法解决实际问题。
Python 自动运维
培训时间:
2018 年 4 月 27-29 日
培训地点:
北京
面向人群:
运维工程师、开发工程师、系统架构师及相关技术支持人员
培训讲师:
熊老师,计算机专业硕士。近 15 年的 IT 领域从事技术研究和项目开发工作。曾在国内外知名的华为技术有限公司中央平台开发部任职,管理测试团队总人数近百人。拥有基于 CMMI、RUP、敏捷开发和测试过程和持续集成的实践经验,以及超过 30 个较大项目(千万元级以上)开发和管理实践经验。通晓多种软件设计和开发工具。现任某大数据公司 CTO,从事大数据分析和数据存储系统方向研发。
课程简介:
本课程主要介绍使用 Python 脚本语言实现管理任务的自动化。首先学习 Python 语言的使用和基本语法、框架。接下来介绍 Python 运维框架的开发。然后详细介绍使用 Python 脚本与操作系统的交互,实现对系统和网络的监控功能。学习使用 Diango 框架以及 Saltstack 和 paramiko、pexpect 这些批量运维管理框架的使用。
课程咨询(王老师)
Tel:13810052112
E-mail:wangkw@vastdata.com.cn
海量数据学院
领先的ABC+职业教育机构
官网:www.abcplus.com.cn
以上是关于AI | 机器学习故事汇-支持向量机 (SVM)的主要内容,如果未能解决你的问题,请参考以下文章