机器学习二十三：scikit-learn 支持向量机算法库总结

Posted 2021-04-26 AI玩转智能

AI

菌

之前通过一个系列对支持向量机(以下简称SVM)算法的原理做了一个总结，本文从实践的角度对scikit-learn SVM算法库的使用做一个小结

scikit-learn SVM算法库封装了libsvm 和 liblinear 的实现，仅仅重写了算法了接口部分

而 libsvm 是台湾大学林智仁教授等开发设计的一个简单、易于使用和快速有效的SVM模式识别与回归的软件包，拥有C、Java、Matlab、Python等数十种语言版本

回顾SVM分类算法和回归算法

我们先简要回顾下SVM分类算法和回归算法，因为这里面有些参数对应于算法库的参数，如果不先复习下，下面对参数的讲述可能会有些难以理解。

　　　　

对于SVM分类算法，其原始形式是：

其中m为样本个数，w , b 是我们的分离超平面的 w∙ϕ(xi)+b=0 系数,  ξi 为第i个样本的松弛系数， C为惩罚系数。ϕ(xi) 为低维到高维的映射函数

通过拉格朗日函数以及对偶化后的形式为：

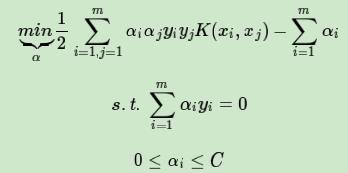
其中和原始形式不同的α为拉格朗日系数向量

对于SVM回归算法，其原始形式是：

，ξi∨，ξi∧为第i个样本的松弛系数，ϵ为损失边界，到超平面距离小于ϵ的训练集的点没有损失

通过拉格朗日函数以及对偶化后的形式为：

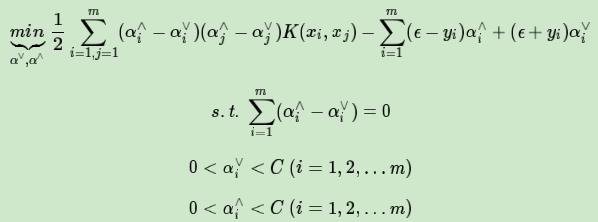
其中和原始形式不同的，α∨，α∧为拉格朗日系数向量

核函数概述

而上面出现的

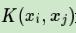
正是我们的核函数。它能够把数据映射到高纬度空间，从而使得一些线性不可分的数据集能用一个超平面分类

而核函数主要有四种：

1）线性核函数 （Linear Kernel）

    表达式为：

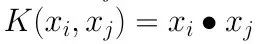
就是普通的内积，LinearSVC 和 LinearSVR 只能使用它

 2）多项式核函数 （Polynomial Kernel）

    表达式为：

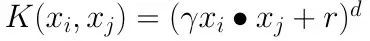
 其中，γ,r,d都需要自己调参定义,比较麻烦

3）高斯核函数（Gaussian Kernel）

    表达式为：

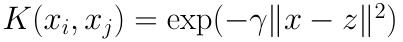
它是libsvm默认的核函数，当然也是scikit-learn默认的核函数。其中，γ大于0，需要自己调参定义

 4）Sigmoid核函数

    表达式为：

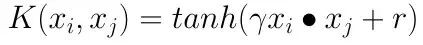
其中，γ,r都需要自己调参定义

　一般情况下，对非线性数据使用默认的高斯核函数会有比较好的效果，如果你不是SVM调参高手的话，也建议使用高斯核来做数据分析

SVM分类算法库使用概述

而scikit-learn中SVM的算法库分为两类，一类是分类的算法库，包括SVC， NuSVC，和LinearSVC 3个类。另一类是回归算法库，包括SVR， NuSVR，和LinearSVR 3个类。相关的类都包裹在sklearn.svm模块之中

对于SVC， NuSVC，和LinearSVC 3个分类的类，SVC和 NuSVC差不多，区别仅仅在于对损失的度量方式不同，而LinearSVC从名字就可以看出，他是线性分类，也就是不支持各种低维到高维的核函数，仅仅支持线性核函数，对线性不可分的数据不能使用

我们这里就以SVC为例，再横向对比NuSVC与LinearSVC的用法（官网API参考：http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC）

首先来我们需要先对SVC函数进行初始化，参数有以下几种：

上面的都是一些默认参数。具体的解释如下：

（1）C: 目标函数的惩罚系数C，C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。默认 C = 1.0；

（2）kernel：参数选择有 ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’和其他可用核函数 , 默认的是"rbf"; 

（3）degree：也就是多项式核函数 ‘poly’中的 d, 决定了多项式的最高次幂； 

（4）gamma：核函数 ‘poly’, ‘rbf’,‘sigmoid’中的 γ , 默认是 γ = 1

（5）coef0：核函数 ‘poly’,‘sigmoid’中的 r 独立项

（6）shrinking ：是否采用shrinking heuristic方法，默认为true

（7）probablity: 可能性估计是否使用(true or false)；

（8） tol ：停止训练的误差值大小，默认为1e-3

（9）cache_size ：核函数cache缓存大小，默认为200。在大样本的时候，缓存大小会影响训练速度

（10）class_weight: 每个类所占据的权重，不同的类设置不同的惩罚参数C, 缺省的话自适应， 主要是为了防止训练集某些类别的样本过多，导致训练的决策过于偏向这些类别；

（11）verbose: 跟多线程有关，不大明白啥意思具体； 

（12）max_iter: 最大迭代次数，默认 = 1， 如果 max_iter = -1, 则将无限进行; 

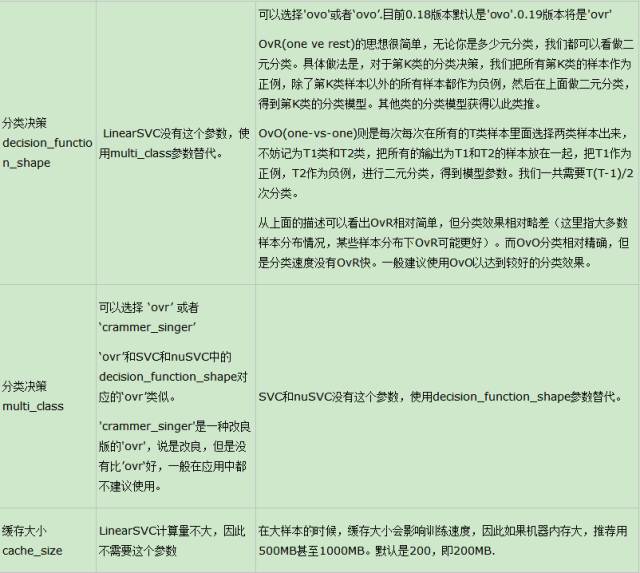
（13）decision_function_shape （分类决策）： ‘ovo’ 一对一, ‘ovr’ 多对多  

        OvR(one ve rest)的具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元分类，得到第K类的分类模型。其他类的分类模型获得以此类推。

        OvO(one-vs-one)则是每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元分类，得到模型参数。我们一共需要T(T-1)/2次分类。

（14）random_state ：用于概率估计的数据重排时的伪随机数生成器的种子。 

在了解这些参数以后让我们把 SVC 与LinearSVC 、NuSVC对比一下：

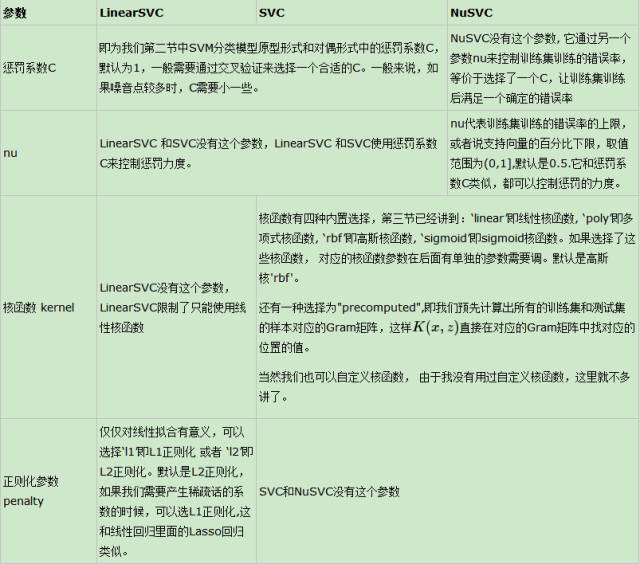
调好参数后，我们就可以使用SVC.函数了，官网给出的有以下几种：

这里我们用一个实例来讲解SVM 分类。首先我们载入数据和类的定义：

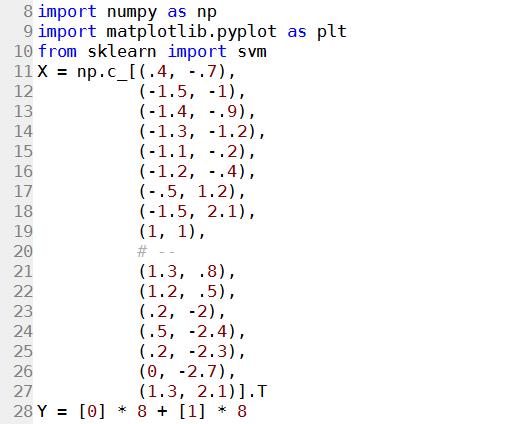
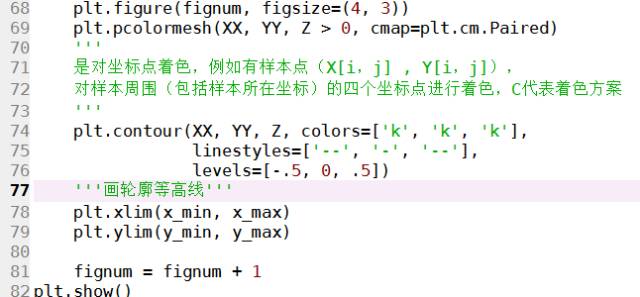
然后我们进行循环：

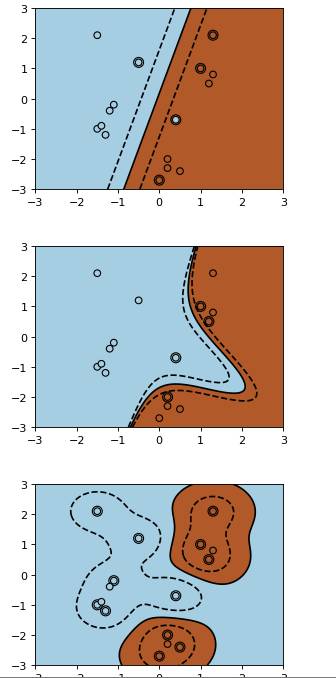
得到的效果如下：

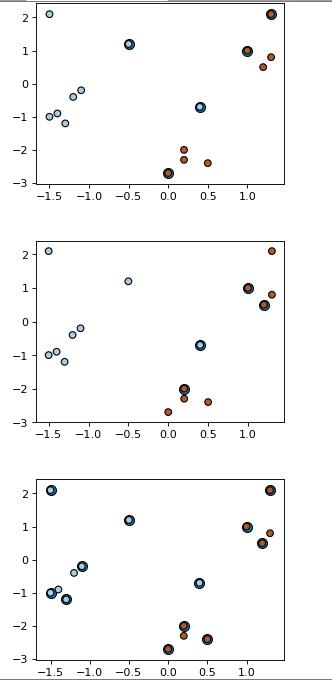
从上面的三张图我们也许看不出三种核的分类有什么区别，不过等我们把支持向量画出来后，就可以体会到了。不过在此之前，还要将两个函数 np.c 与 np.mgrid

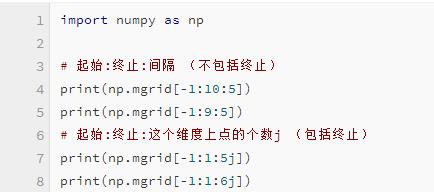
然后又是np.c

所以接下里我们就有了：

在处理好所有数据后，我们就有了：

这样就很容易看出核函数的区别了

SVM回归算法库使用概述

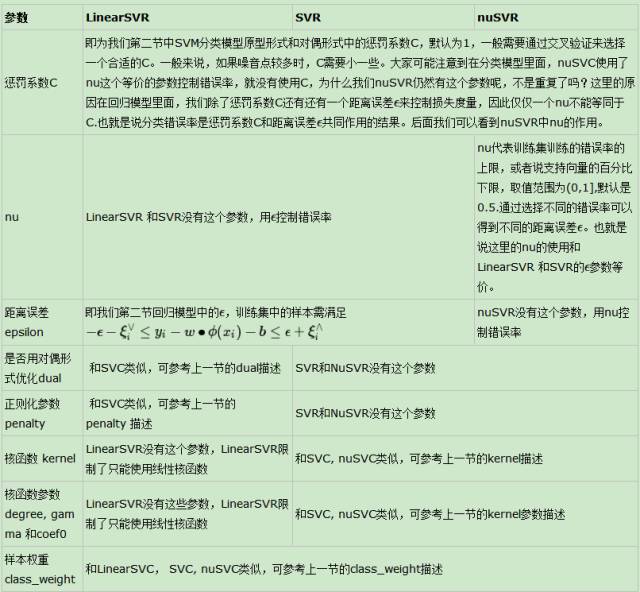
同样的，对于SVR， NuSVR，和LinearSVR 3个回归的类， SVR和NuSVR差不多，区别也仅仅在于对损失的度量方式不同。LinearSVR是线性回归，只能使用线性核函数

由于SVM回归算法库的重要参数巨大部分和分类算法库类似，因此这里重点讲述和分类算法库不同的部分，对于相同的部分可以参考上一节对应参数。

我们这里就以SVR为例，再横向对比NuSVR与LinearSVR的用法（官网API参考：http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html#sklearn.svm.SVR）

首先来我们需要先对SVC函数进行初始化，参数有以下几种：

上面的都是一些默认参数，与SVC的区别不大。就各位自行体会了

主要的属性如下；

横向对比结果：

接下来这里我们也用一个实例来讲解SVM 回归。首先我们载入数据和类的定义：

这里也有几个值得注意的函数：

    1）np.sort 和 np.sorted

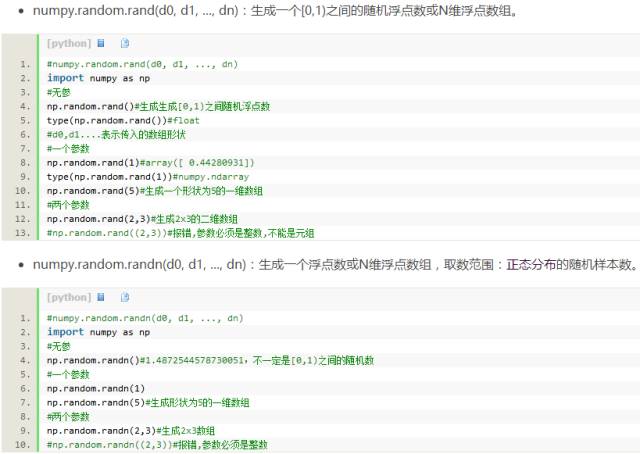
    2）np.random.rand与np.random.rand

    3)  np.ravel 与 np.flatten

首先声明两者所要实现的功能是一致的（将多维数组降位一维），两者的区别在于返回拷贝（copy）还是返回修改后的样本

接下来就是对数据进行拟合：

在画出图像前，让我们先看看一个函数。

当你将很多个曲线画在一张图上时，自动产生的legend矩形框往往会覆盖住已经画出来的曲线，很不美观，这时你就需要写专门的代码对legend的位置进行精确的控制，而不能再依靠系统帮你自动控制了

所以我们使用：plt.legend()，其熟悉可以参考官网说明：http://matplotlib.org/api/legend_api.html#matplotlib.legend

还有：matplotlib中legend位置调整：http://blog.csdn.net/robertchenguangzhi/article/details/49719467

最后画出图像进行对比：

我们可以看到：

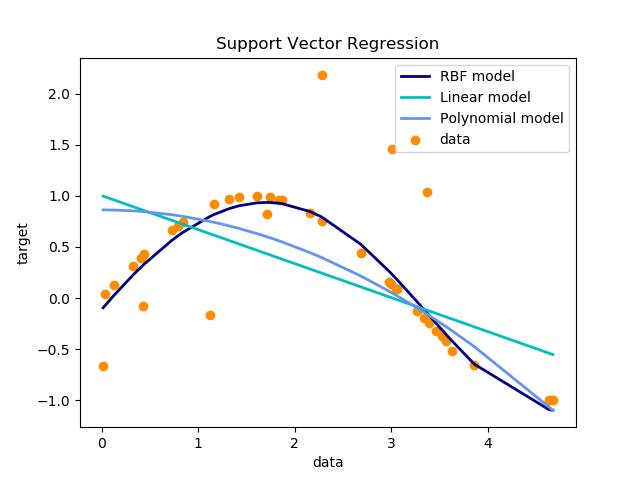
这就是三种核函数进行回归产生结果的不同

帮助

上面面已经对scikit-learn中类库的参数做了总结，这里对其他的调参要点做一个小结。

　　　　1）一般推荐在做训练之前对数据进行归一化，当然测试集中的数据也需要归一化。。

　　　　2）在特征数非常多的情况下，或者样本数远小于特征数的时候，使用线性核，效果已经很好，并且只需要选择惩罚系数C即可。

　　　　3）在选择核函数时，如果线性拟合不好，一般推荐使用默认的高斯核'rbf'。这时我们主要需要对惩罚系数C和核函数参数γ进行艰苦的调参，通过多轮的交叉验证选择合适的惩罚系数C和核函数参数γ。

　　　　4）理论上高斯核不会比线性核差，但是这个理论却建立在要花费更多的时间来调参上。所以实际上能用线性核解决问题我们尽量使用线性核。

不失初心，不忘初衷

AI玩转智能