一次简单的报告：机器学习之支持向量机SVM

Posted 2021-04-26 无敌心心酱

  上次组会我简单的报告了一下支持向量机，自学的不深，但对想入门了解的小伙伴来说应该是有帮助哒~ 因为我的报告非常简单哈哈！

  首先介绍一下我报告的框架：

接下来就是干货啦~~

一、 什么是机器学习？

1. 学习→机器学习

大家先思考一个问题：什么是“学习”？学习是我们通过观察获得技能的一个过程，那么什么是“机器学习”呢？机器学习和我们人类学习是一个道理，只不过他们是用资料data来进行学习。

2.   机器学习的规律

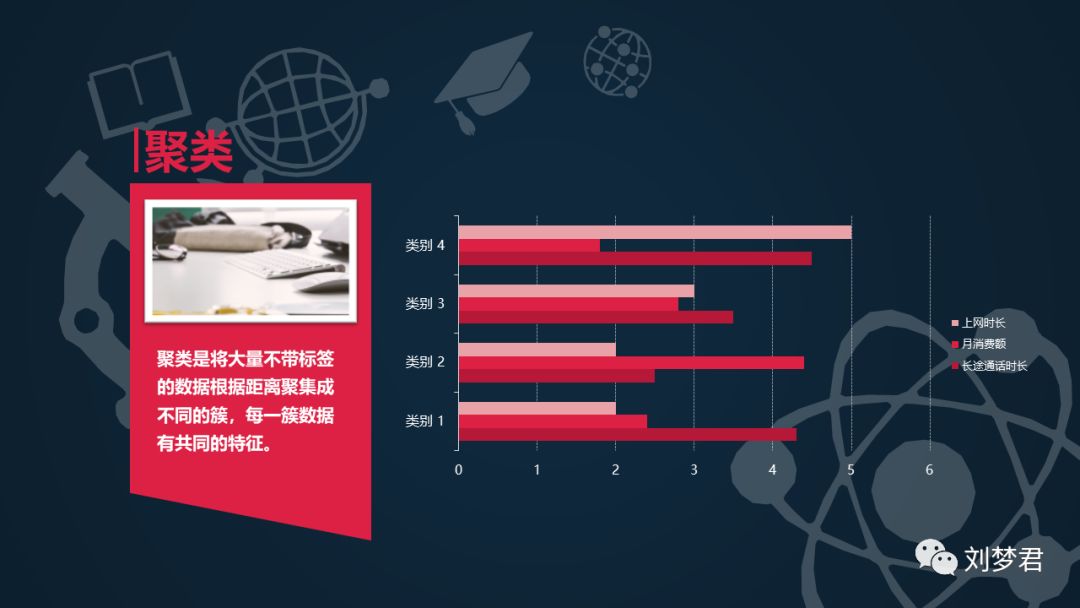
机器学习是从大量数据中学习出特定规律的算法。其中提到的规律有很多种，比如分类、聚类、回归、关联分析等。

分类就是给定大量带标签的数据，计算出未知标签样本的标签取值。如年龄 40 岁以上、工科、研究生以上学历，这类人薪资水平是高收入；年龄 20-30 岁、文科、大专学历，这类人的薪资水平是低收入；现有一位 23 岁大专文科人士麦某，求该人的薪资水平是哪类？根据分类建模，就可以知道这个人的薪资水平很可能是低收入。

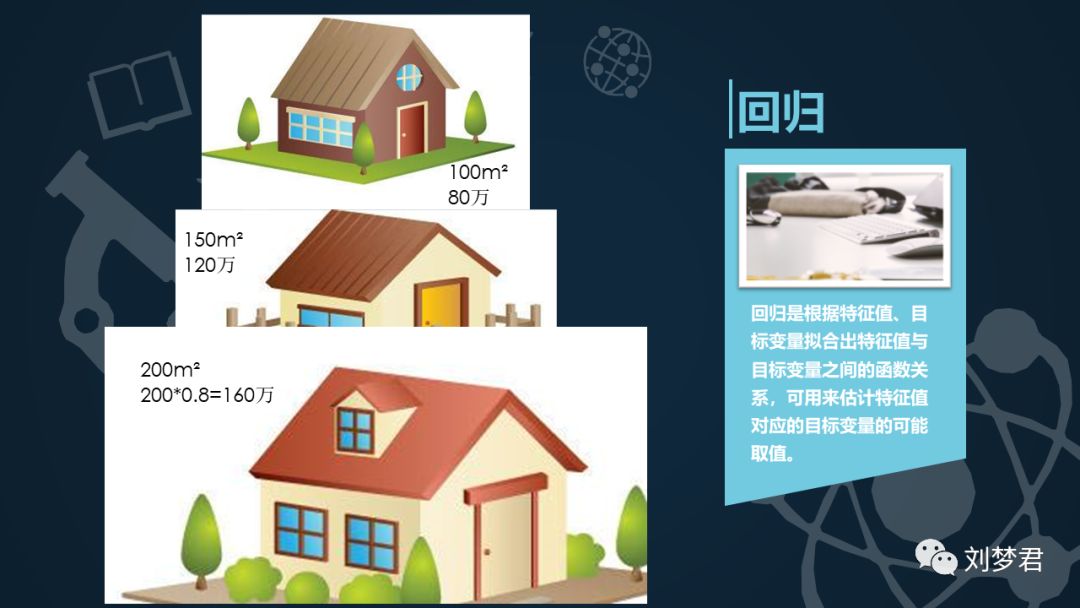
回归是根据特征值、目标变量拟合出特征值与目标变量之间的函数关系，可用来估计特征值对应的目标变量的可能取值。举个简单的例子，某市今年某 100 平米的房子价格是 80 万，某 150 平米房子价格是 120 万，那么某 200 平米的房子价格的取值就可能是 200*0.8=160 万左右。

关联分析是计算出大量数据之间的频繁项集合。如超市订单中有大量订单同时包含啤酒与尿布，这其中的频繁项就是啤酒和尿布，那么超市就可以针对这个规律对啤酒和尿布进行组合促销活动。

分类算法主要包括 K 近邻、决策树、朴素贝叶斯、逻辑回归、支持向量机、AdaBoost 等；回归主要包括线性回归、岭回归、lasso、树回归等；聚类主要包括 K-Means 以及它的各种变形算法；关联分析主要包括 Apriori、FP-growth 等算法。

支持向量机即 support vector machine(简称 SVM)，是机器学习领域经典的分类算法。

 

二、什么是支持向量机？

1. SVM的定义

支持向量机(Support VectorMachine，SVM)是Corinna Cortes和Vapnik等于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

在机器学习中，支持向量机（SVM，还支持矢量网络）是与相关的学习算法有关的监督学习模型，可以分析数据，识别模式，用于分类和回归分析。

（这样说的话可能大家会一脸懵逼，那我们通过一个小故事来理解一下吧~~）

2.   魔鬼和王子的故事

      很久很久以前，有一个魔鬼抓走了一位漂亮的公主，王子要去救公主回来。

魔鬼对王子说：你能用一根棍子把这堆球区分开么？

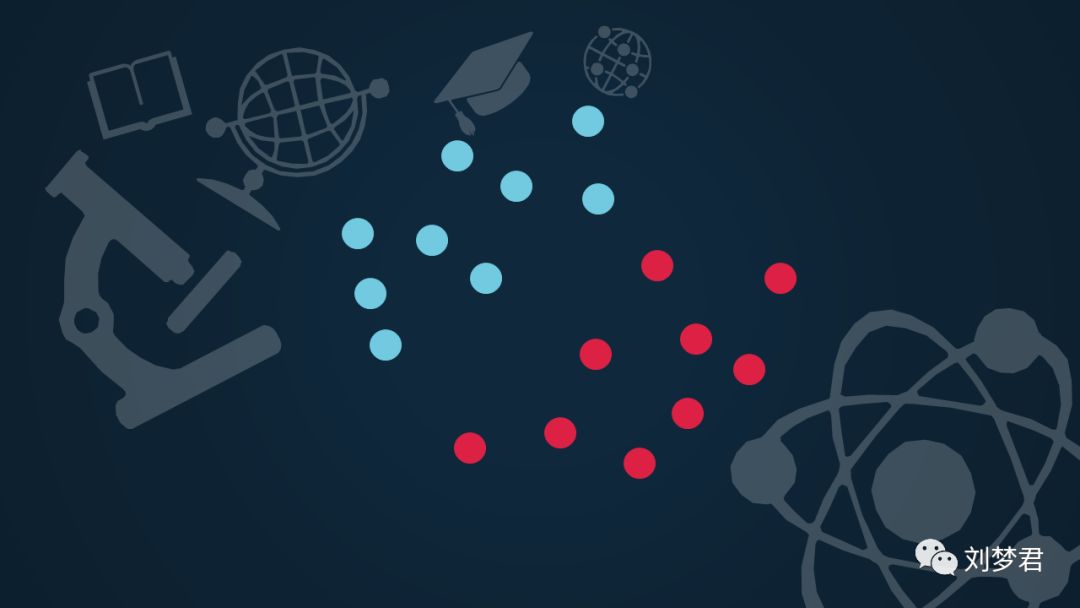
王子很容易的就把它们分开了。

这时魔鬼又放了几个球，结果有的球就跑错了阵营。

于是王子恳求魔鬼再给他一次机会。王子重新拜访了木棍的位置，这次魔鬼放的球就依然能够被很好的区分开了。

魔鬼为了刁难王子，又给了他这样的一堆球：

王子见状，一把拍起这堆球，待球飞起时，迅速用一张纸放在中间，分开了两拨球。

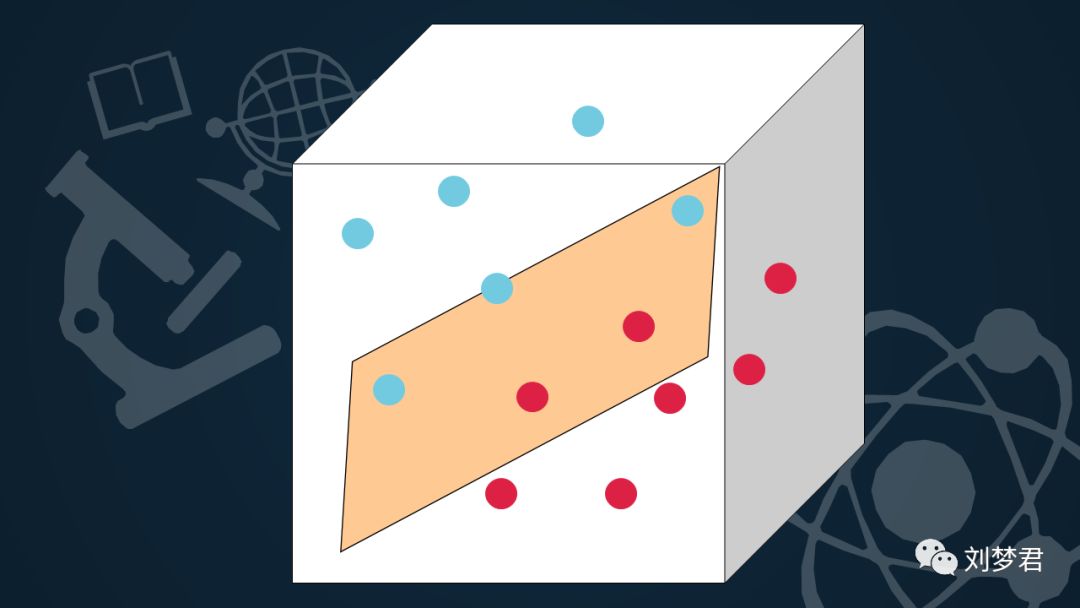
魔鬼不得不佩服王子的机智，于是放了公主，从此王子和公主幸福快乐的生活在了一起。。。

3.   引入概念：

     

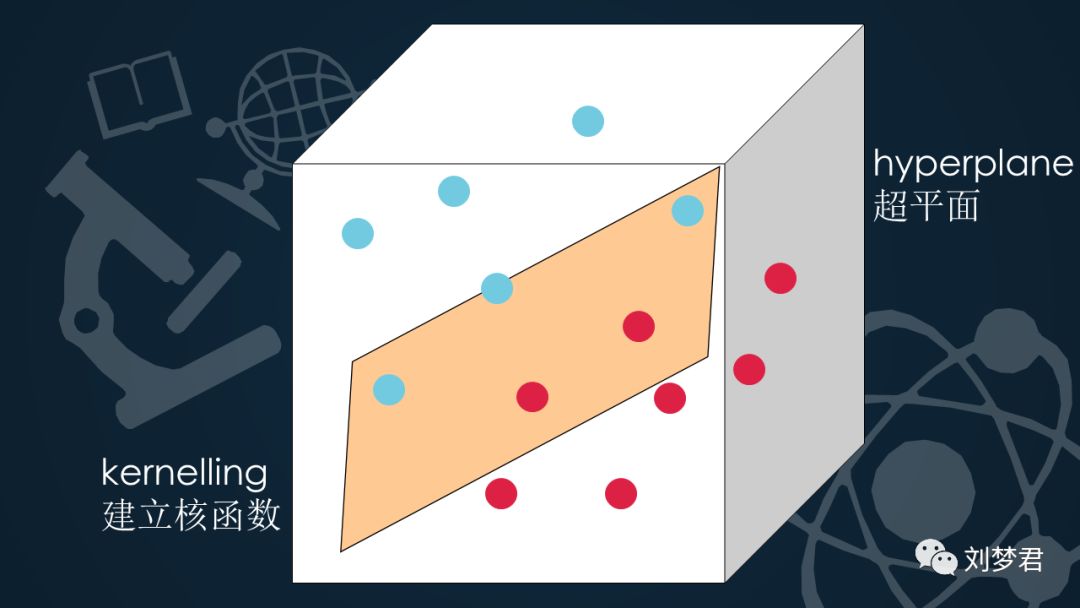
1）超平面：

在几何体中，超平面是一维小于其环境空间的子空间。如果空间是3维的，那么它的超平面是二维平面，而如果空间是二维的，则其超平面是一维线。所以它是平面中的直线，是空间中的平面。是直线的推广。其表现形式是：W^TX+b=0

在二维中是直线，a*x+b*y+c=0;

在三维中是平面，a*x+b*y+c*z+d=0;

推广到n维空间，a*x+b*y+c*z+…+k=0.

(a,b,c)是向量w,是由平面确定的数。 xyz是平面上任意一点的坐标，也是向量。

2）线性分类器：

从数学表达式来看，线性分类器就是一个函数：y=f（x）=W^Tx+b ，

其中X表示特征，y表示类别。

举一个二维空间超平面的例子，此时超平面也就是一条直线。首先看这张图：

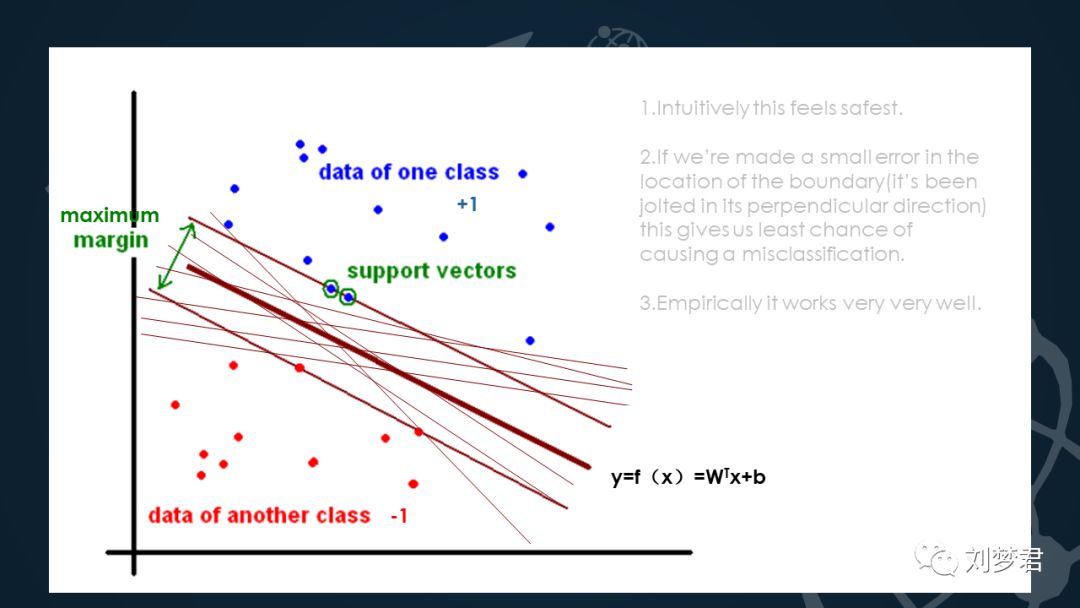
数据点用x表示，这个x是一个n维向量；类别用y表示，在这里我们把类别取+1和-1 ，比如说蓝点表示+1，红点表示-1。选择+1和-1是为了方便SVM公式的推导。

   首先我们希望的是，根据超平面把数据分隔开，使超平面的一边，y全是+1，另一边全是-1。我们怎么来分这些数据呢？这条线是一种分类的方法，但是也可以这样分…都看着像是正确的分类方法，但是哪样才是最佳的呢？前面我们说过，超平面是用来分类两类数据的，越接近平面的点，越难分隔，如果超平面稍微转动一下，他们就有可能跑到另一边了。因此从几何直观上来说，我们希望正负样本分的越开越好。也就是说正负样本之间的间隔越大越好。因为距离超平面越近的样本，分类器的置信度也就越低。我们所说的SVM的优化目标，也就是最大化分类的点的分类超平面的距离。这样能达到更好的分类效果。

如果我们令y=f（x）=W^Tx+b  当f(x)=0时，x就是位于超平面上的点。在这里我们假设所有满足f(x)<0的点的类别是y=-1,那么f(x)>0的数据点就对应y=+1的数据点。

   所以现在引入分类间隔的概念。Maximum Margin，是带有最大间隔的线性分类器，这是最简单的一种支持向量机的形式，这个分隔是指超平面到达第一个数据点的边界的宽度。这些边缘线上的数据点就叫做支持向量，这也是支持向量机名称的由来。可能会有人问：为什么要以最大间隔作为最优化呢？原SVM作者给出了几个原因：1.它直觉上是安全的，2.它给了我们犯错误的机会，如果它在边界附近转动可能不会造成分类的混乱。3.实验证明它的确工作的很好。

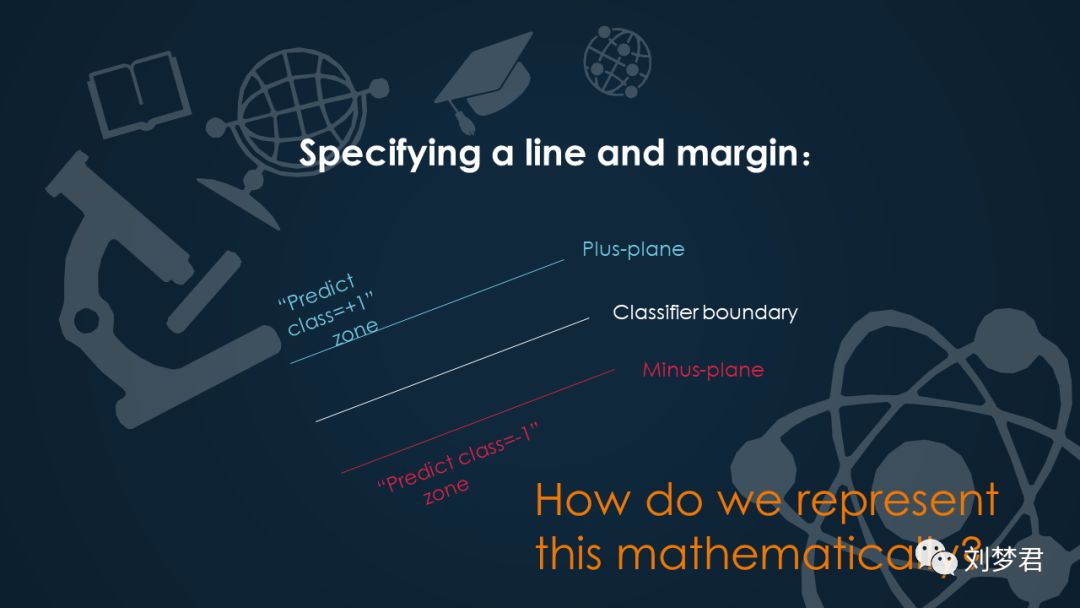
   3）Specifying a line andmargin：

现在来简单的说一下线性分界线的间隔。上面的区域是类别为+1的超平面分界线，上面这部分区域表示类别为+1的预测空间；下面的区域是类别为-1的超平面分界线，下面表示类别为-1的预测空间。那么我们如何用数学表达式来表示这个？

在类别为+1的线性函数中，我们可以这样表示它的函数关系式：plus-plane={x: W.X +b=+1}，同理我们也可以得到类别为-1的线性函数表达式：minus-plane={x: W.X +b=-1}。根据这个我们可以把数据分为三种：

classify as… +1 if W.X+b>=1 

          -1 if W.X +b<=-1

Universe if -1< W.X +b<1

一种是类别+1，一种是类别-1，还有一种是在分界线上的。

用M来表示间隔宽度，那么我们怎么用W和b来计算M呢？

省略公式推导过程（我也不会。。）

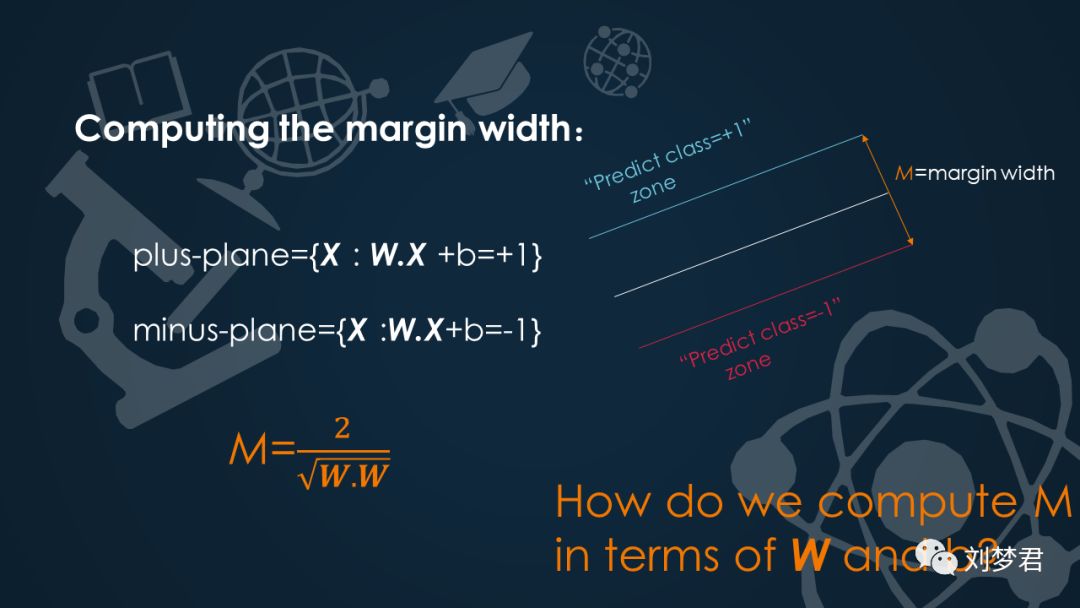
4.   SVM 基本原理

SVM 原理分为软间隔最大化、拉格朗日对偶、最优化问题求解、核函数、序列最小优化 SMO 等部分。虽然这些名词看起来很晦涩，但是深入探索后可能就会发现其中的思想并没有那么复杂。(然而我感觉实在是很复杂，数学公式都看不懂…) 感兴趣的童鞋可以自行深入学习之….Good Luck