05-支持向量机 (SVM) 上
Posted 机器学习算法和人工智能
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了05-支持向量机 (SVM) 上相关的知识，希望对你有一定的参考价值。
1. 背景：
1.1 最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出
1.2 目前的版本(soft margin)是由Corinna Cortes 和 Vapnik在1993年提出，并在1995年发表
1.3 深度学习 (2012)出现之前, SVM被认为机器学习中近十几年来最成功, 表现最好的算法
定义：在1963年提出的一种新的非常有潜力的分类技术, SVM是一种基于统计学习理论的模式识别方法，主要应用于模式识别领域.
2. 机器学习的一般框架：
训练集 => 提取特征向量 => 结合一定的算法 (分类器: 比如决策树, KNN) =>得到结果.
3. 介绍：
3.1 例子：
两类？哪条线最好？
3.2 SVM寻找区分两类的超平面(hyper plane),使边际(margin)最大
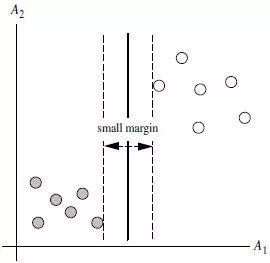
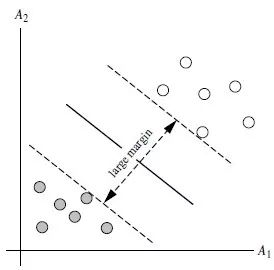
-总共可以有多少个可能的超平面？无数条
-如何选取使边际(margin)最大的超平面(Max Margin Hyperplane)？
-超平面到一侧最近点的距离等于到另一侧最近点的距离, 两侧的两个超平面平行
3.3 线性可区分(linear separable)和线性不可区分(linear inseparable)
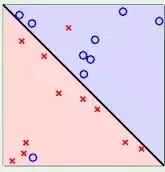
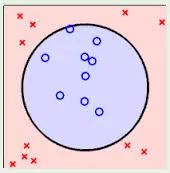
4. 定义与公式建立
超平面可以定义为：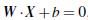
(W: weight vectot)
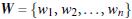
n 是特征值的个数
X: 训练实例
b: bias
4.1 假设2维特征向量：X = (x1, X2)
把 b 想象为额外的 wight
超平面方程变为: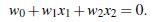 
所有超平面右上方的点满足: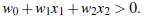
所有超平面左下方的点满足: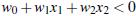
调整weight，使超平面定义边际的两边:
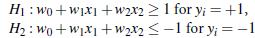
综合以上两式, 得到 (1):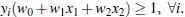 
所有坐落在边际的两边的超平面上的点被称作”支持向量"
分界的超平面和H1或H2上任意一点的距离为: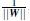 
(i.e.: 其中||W||是向量的范数(norm))
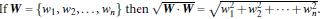
所以, 最大边际距离为: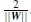 
5. 求解
5.1 SVM如何找出最大边际的超平面呢(MMH)？
利用一些数学推导,以上公式 (1) 可变为有限制的凸优化问题(convex quadratic optimization)
利用 Karush-Kuhn-Tucker (KKT)条件和拉格朗日公式，可以推出MMH可以被表示为以下“决定边界 (decision boundary)”
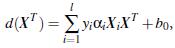
其中:
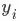是支持向量点 
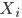(support vector)的类别标记(class label)
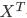是要测试的实例
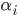和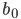
都是单一数值型参数,由以上提到的最优算法得出
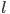是支持向量点的个数
5.2 对于任何测试(要归类的)实例,带入以上公式,得出的符号是正还是负决定
6. 例子:
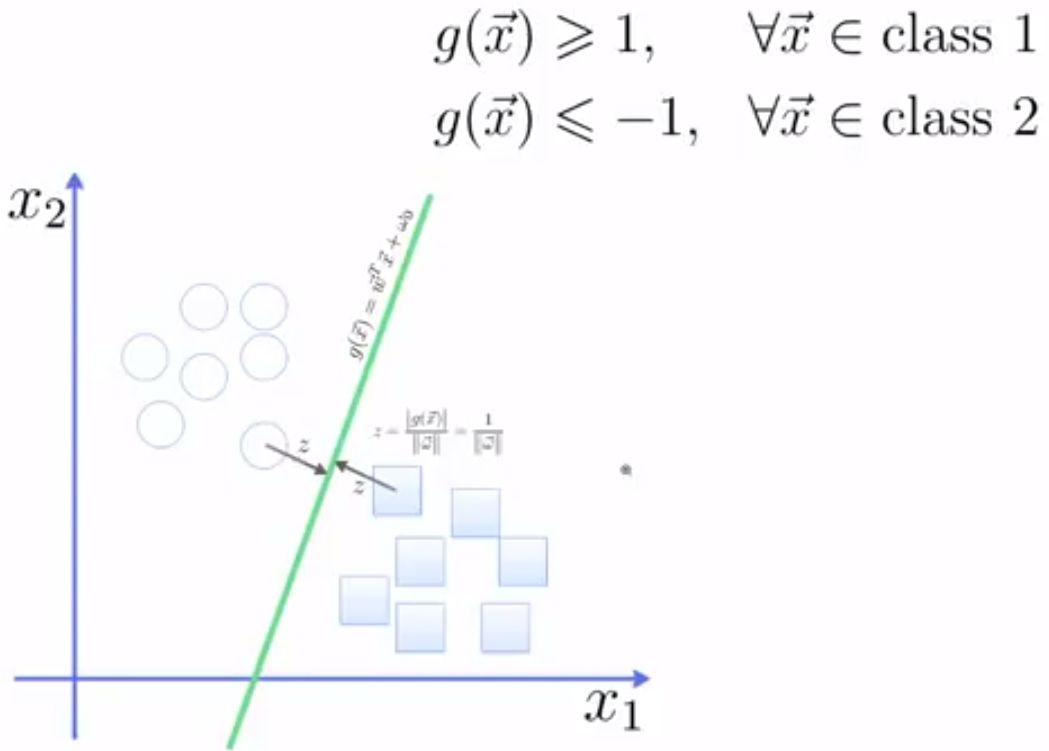
SVM 的应用-上
实践：案例一（简单认识SVM）
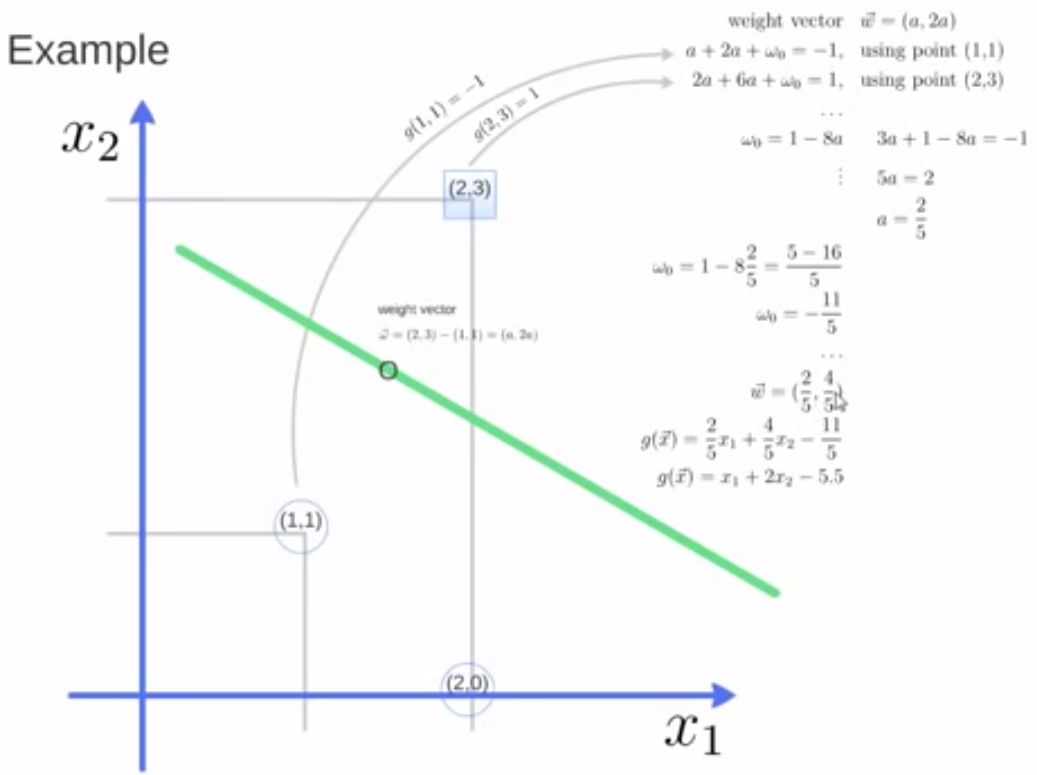
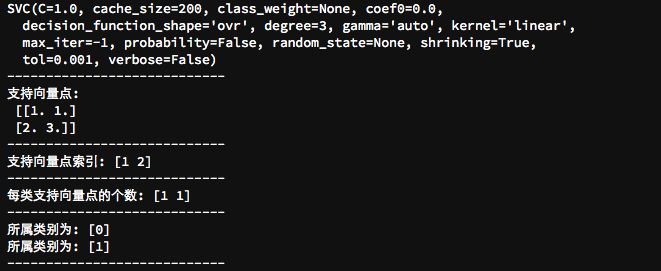
项目代码及运行结果：
运行结果:
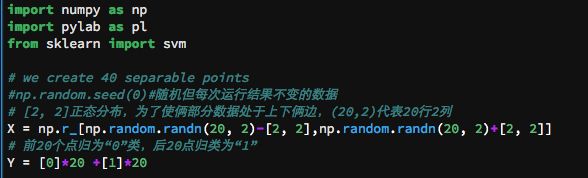
实践：案例二（复杂数据的线性可区分）
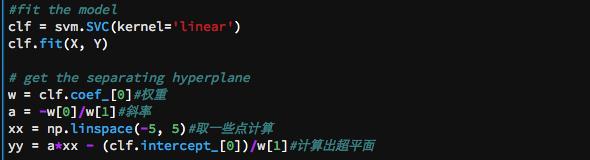
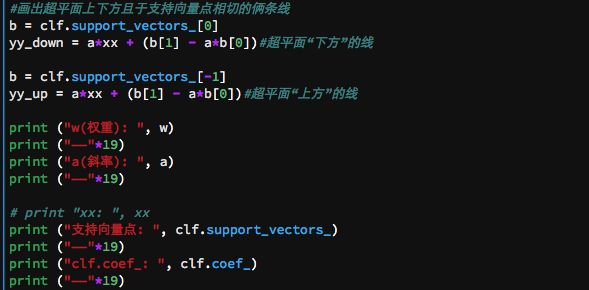
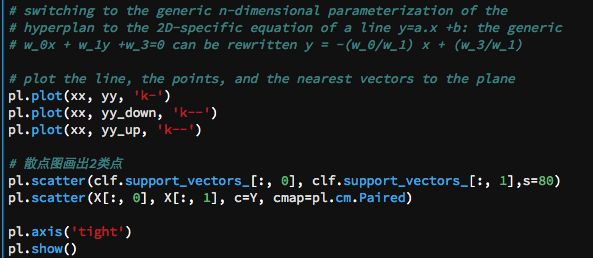
运行结果:
以上是线性可分的 SVM 的俩个小案例，如有错误欢迎指出和改正
以上是关于05-支持向量机 (SVM) 上的主要内容，如果未能解决你的问题，请参考以下文章