支持向量机(第三章)

Posted 2021-04-26 易智能EasyAI

第三章 SVM最优化问题

SVMs寻找最优超平面

感知器有几个优点：它是一个简单的模型，算法非常容易实现，有相关理论证明可以找出一个分类数据的超平面。然而，它有一个最大的问题是每次都不能找到相同的超平面。我们为什么关心这个？因为并不是所有的超平面都是等价的。如果感知器得到的超平面非常接近一类接据点，你有权利相信它很难推广来适应新的数据。

SVMs 没有这个问题。事实上，相反要寻找惟一超平面，SVMs 尝试去寻找这个超平面。我们称它为最优超平面，我们将说它是惟一的能最好的分割数据。

我们怎样比较两个超平面？

因为我们不能凭感觉选择最优超平面，我们需要有一个排序标准来比较两个超平面哪一个更好。

在本章接下来的部分，我们将试着去了解怎样比较两个超平面。另外，我们将找到一个方法去计算出一个能告诉我哪个超平面能量好的分类数据的数值。我们将要看到这些方法是如何工作的，但是现在我们可以先看它们为什么不能工作而正确的找出它们的局限。让我们试着从一个例子仅用超平面的方程式去比较两个超平面。

使用超平面方程式

给出一个示例和一个超平面，我们希望知道这个示例与超平面的关系。

一个关键要素是我们已经知道如果x的值满足这个直线方程，就说明它在这条直线上。同理对于一个超平面：对于数据点x和一个超平面定义于一个向量w和偏置b，如果x在超平面上，我们将得到。

但是如果点不在超平面上将发生什么呢？

让我们从一个实例来看发生了什么。在图22中，直线定义于和b=9。我们应用超平面方程式：

· 对于点A（1，3），代入向量a=（1，3）我们得到

· 对于点B（3，5），代入向量a=（3，5）我们得到

· 对于点C（5，7），代入向量a=（5，7）我们得到

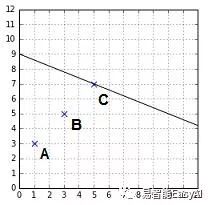
图22：通过方程式，A 返回的结果比B大

你们可以看到，当点不在超平面上时我们得到的结果值不等于0。事实上，如果点离超平面越远，我们得到的结果值比靠近超平面的点返回的值大。

另一个需要注意的是方程式返回的结果的符号能告诉我们点相对于直线的位置。用这个直线方向我们能得到图23所示的结果，我们得到：

· 点A（3,5）返回2.8

· 点B（5,7）返回0

· 点C（7,9）返回-2.8

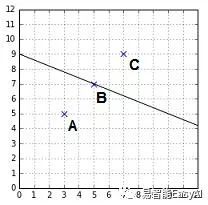
图23：通过方程式，C返回一个负值

如果方程式返回正值，这个点在直线的下方，当它返回一个负值时，这个点在直线的上方。注意在视觉上的上方或下方并不是必要的，比如图24所示的直线，它将是左边或右边，但是在逻辑上是相同的。超平面方程返回的值的符号可以告诉我们两点处于同一边。事实上，这就是我们第二章定义的假设函数要做的事情。

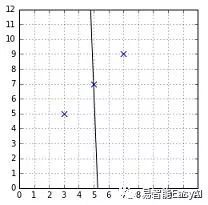
图24：直线可以不同的方式分割空间

我们现在开始有一个解决方法来比较两个超平面。

给出一个训练示例（x,y）和一个定义于向量w和偏置b的超平面，我们计算数值来知道这个点与超平面的的距离。

给出数据集，我们计算每一个训练示例的，定义数字B为中的最小值。

如果我们要在两个超平面中选择一个时，我们要选择一个最大值的B。

很简单，意思是我们有k个超平面，我们将计算和选择返回值为的超平面。

示例返回负值的问题

不幸的是，使用用超平面方程返回值有它的局限性。在方式程返回负值时选最小值就不正确了（方程式返回负值的分类）。

记住，我们总是希望返回值的点靠近超平面。B在示例返回的都是正值时工作得很好。从=+5和=+1这两点中，我们选择一个小的，所以我们选+1。然后，当示例返回=-5和=-1时，我们将选择-5因为-5比-1小，但是最接近的点实际上是=-1。

一个修正这个问题的考虑是取的绝对值。

给出一个数据集，我们遍历示例计算然后说B是中绝对值最小的数：

这个超平面能正确分类数据码？

计算数字B让我们可以选择一个超平面。但是，仅仅只是用这个数值，我们可能选出一个错误的。考虑图25所示：这是一个正确的分类，而且这个B是用后一个公式算出来的2。

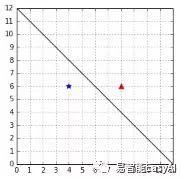
图25：正确分类数据的超平面

在图26中，示例数据被错误分类，但是这个B的值也是2。这个问题在于我们用B选出来的平面我们不知道哪一个是对的。理论上，它们看起来都很好，但是事实上，我们希望选择图25中的超平面。

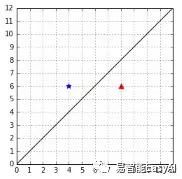
图26：错误分类数据的超平面

碰到这种情况如何调整我们的公式？

很好，在我们的训练数据（x,y）中有一个部分没有使用：就是这个y!

如果我们用来乘以y，改变一下记与，让我们称这个新的数为f：

f的符号总是：

· 正值表示这个点被正确分类

· 负值表示这个点被错误分类

给出一个训练集, 我们可以计算：

使用这个公式，当比较两个超平面时，我们可以一直选择F最大的哪个。增加的功能可以让图25和图26这种情况下，我们也总能选出正确分类的超平面（因为F将是一个正值，负值将是另外的平面）。

在文献里，数字f有一个名字，它被称为示例数据的函数间隔（functional margin）;它的数值可以用Python计算，如代码表19所示。类似的，数字F就是数据集的函数间隔。

代码表19

# Compute the functional margin of an example (x,y)

# with respect to a hyperplane defined by w and b.

def example_functional_margin(w, b, x, y):

result = y * (np.dot(w, x) + b)

return result

# Compute the functional margin of a hyperplane

# for examples X with labels y.

def functional_margin(w, b, X, y):

return np.min([example_functional_margin(w, b, x, y[i])

for i, x in enumerate(X)])

用这个公式，我们发现这个超平面的函数间隔在图25中是+2，而在图26中是-2。因为它的间隔要大，所以我们选择第一个。

提示：记住，我们希望选择的是具有最大间隔的超平面。

比率不变性

看起来这次我们找到了一个好的方法去比较两个超平面。然而，函数间隔有一个重要的问题：没有比率不变性。

给出一个向量和偏置，如果我们用10来乘它们，我们得到和。我们说我们等比例放大了它们。

向量和，表示同一个超平面因为它们的单位向量相同。这个超平面与向量w正交，它不关心向量的长度。重要的是它的方向，之前在第一章我们称它为单位向量。而且，我们从直角坐标系中可以看到这个超平面与纵坐标的截距是（0，b/），所以我们等比例放大b并没有改变超平面。

这个问题，我们可以看代码表20，当我们计算的函数间隔时，我们给出的数据是的10倍。意思是对于任一超平面，只是等比例放大w和b，我们将找到一个大的函数间隔。

代码表20

x = np.array([1, 1])

y = 1

b_1 = 5

w_1 = np.array([2, 1])

w_2 = w_1 * 10

b_2 = b_1 * 10

print(example_functional_margin(w_1, b_1, x, y)) # 8

print(example_functional_margin(w_2, b_2, x, y)) # 80

解决这个问题，我们只要去做一个小的调整。我们将用单位向量来代替向量w。这样，我们将用w的范式来除w。同样我们将用w的范式来除b平维持比率不变性。

再看求函数间隔的公式：

我们修改后变为一个新的数 γ：

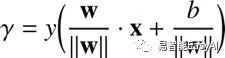
之前，给出一个数据集，我们可以计算：

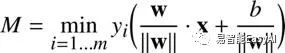
γ的优势在于它能给我们一个相同的数而不用在乎w的值的大小。数γ还有一个名称——它被称为学习示例的几何间隔，M就是这个数据集的几何间隔。一个Python实现如代码表21。

代码表21

# Compute the geometric margin of an example (x,y)

# with respect to a hyperplane defined by w and b.

def example_geometric_margin(w, b, x, y):

norm = np.linalg.norm(w)

result = y * (np.dot(w/norm, x) + b/norm)

return result

# Compute the geometric margin of a hyperplane

# for examples X with labels y.

def geometric_margin(w, b, X, y):

return np.min([example_geometric_margin(w, b, x, y[i])

for i, x in enumerate(X)])

我们可以验证几何间隔可以达到预期。在代码表22中，对于向量和等比放大的向量，函数返回相同的结果。

代码表22

x = np.array([1,1])

y = 1

b_1 = 5

w_1 = np.array([2,1])

w_2 = w_1*10

b_2 = b_1*10

print(example_geometric_margin(w_1, b_1, x, y)) # 3.577708764

print(example_geometric_margin(w_2, b_2, x, y)) # 3.577708764

被称为几何间隔是因为我们能通过几何方式推出这个公式。它可以测量向量x和超平面之间的距离。

在图27中，我们看到点是X在超平面上的正交投影。我们希望找到X和之间的距离d。

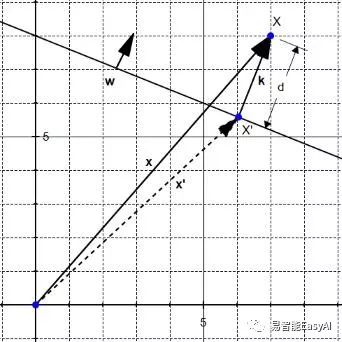
图27：几何间隔就是点X与超平面之间的距离d

向量k与向量w的方向相同，所以它们有相同的单位向量。我们知道k的范式是d，所以向量k可以定义为。

而且，我们可以看到，所以我们可以消掉k和做一些代数计算，我们得到：

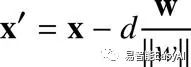
现在，点在超平面上，意味着满足超平面方程式，而且我们有：

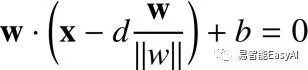
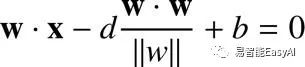
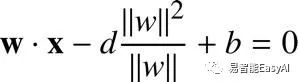
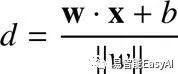
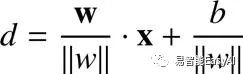
最终，像我们之前一样，我们用y来乘来确保我们选择的超平面可以正确的分类数据，而且它给出几何间隔方程式如我们之前所见：

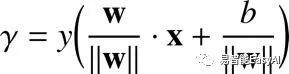
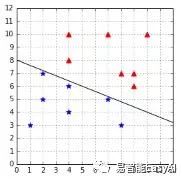
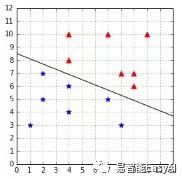
图28：定义为w=(-0.4,-1)和b=8的超平面 图29：定义为w=(-0.4,-1)和b=8.5的超平面

现在我们有定义好的几何间隔，让我们看它是如何来比较两个超平面的。我们可以看到图28中的超平面更接近蓝色星示例比红色三角示例与图29相比较。结果，我们得出它的几何间隔更小。代码表28用代码表21定义的函数来计算每一个超平面的几何间隔。然后得出图29的定义为w=(-0.4,-1)和b=8.5的超平面的几何间隔较大（0.64>0.18）。所以我们选择这个超平面。

代码表23

# Compare two hyperplanes using the geometrical margin.

positive_x = [[2,7],[8,3],[7,5],[4,4],[4,6],[1,3],[2,5]]

negative_x = [[8,7],[4,10],[9,7],[7,10],[9,6],[4,8],[10,10]]

X = np.vstack((positive_x, negative_x))

y = np.hstack((np.ones(len(positive_x)), -1*np.ones(len(negative_x))))

w = np.array([-0.4, -1])

b = 8

# change the value of b

print(geometric_margin(w, b, X, y)) # 0.185695338177

print(geometric_margin(w, 8.5, X, y)) # 0.64993368362

我们看到计算不同超平面的几何间隔，只要修改w和b的值就可以了。我们可以试着稍微增加一下它们的值看看是否能得到大些的几何间隔，但是它是随机的，并且会花大量的时间。我们的目标是在所有可能的超平面中找到一个最优超平面来分类数据，而且这样的超平面有无限多个。

提示：寻找最优以超平面等同于找到最大的几何间隔的w和b的值。

我们怎样才能找到产生最大几何间隔的w的值呢？幸运的是，数学家们设计了工具来解决这种问题。要寻找w和b，我们需要解决什么叫最优化问题。在了解最优化问题如何应用于SVMs前，让我们先快速浏览什么是最优化问题。

什么是最优化问题？

无约束最优化问题

最优化问题的目标是去找到使函数最小化或最大化的变量x（意思是，寻找x的值使函数返回最小或最大值）。实例，我们希望寻找函数的最小值问题可以写成：

或，可这样表示：

在这个例子中，我们要自由的搜索所有可能的x的值。我们说这个问题是无约束的。我们可以看图30，在x=0处得到函数的量小值为0。

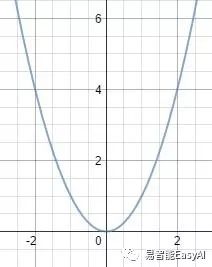图30：无约束时，最小值为0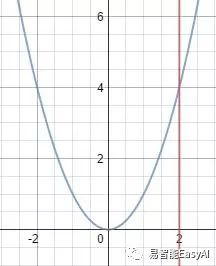

图31：因为约束条件为x-2=0，最小值为4

有约束最优化问题

唯一等式约束

有时我们对方程本身的最小值不感兴趣，但是经常遇到带有约束条件的最小值。在某些例子中，我们增加一个约束条件通过 subject to 来表示这个问题，也常常简写成s.t。例如，假如我们希望知道f的最小值但是限定x为一特定值，我们可以写成：

这个例子表示在图31中。通常，约束条件被写成右边为0的等式像这个问题可以写成：

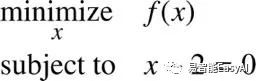
用这个记法，我们清楚的看到约束是一次方程而目标函数f是一个二次方程。因此我们称这个问题为二次最优化问题或是一个二次过程问题。

可行集

满足这个问题的约束条件的变量集合被称为可行集（或可行区域）。当解这个最优化问题时，解必须满足可行集。在图31中，可行集约束仅有一个变量，所以这个问题不复杂。然而，当我们要处理的函数有多个变量，像，它让我们知道要从许多值中试着去求最小值（或最大值）。

例如：

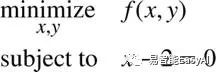
在这个问题中，可行集是所有成对的点（x,y），像这样。

多等式约束和向量表示

我们可以任意增加多个约束条件，在下面的例子是方程有三个约束条件的最优化问题：

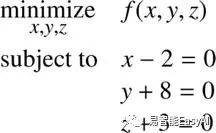
当我们有多个变量时，我们可以用向量表示去提高可读性。用向量让方程变为，这个问题就可以写为：

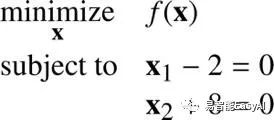
我们增加约束，头脑中要想着去减少可行集。如果一个解被求出，所有的条件都必须满足。

例如，我们看下面的问题：

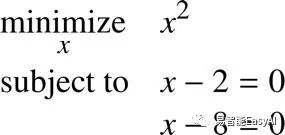
我们可以想象x=2和x=8是解，但这不符合事实。当x=2，约束条件x-8=0就不适合；并且法x=8，约束条件x-2=0就不适合。这个问题是无解的。

提示：如果在部题中加入过多的约束条件，它可能会变为无解的。

如果你增加约束条件改变一个最优化问题，将使优化结果变糟，或者，最好，你不要改变它（Gershiwin,2010）。

不等式约束

我们可以用不等式做为约束条件：

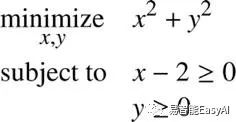
而且我们可以组合等式约束和不等式约束：

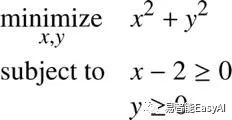
我们怎样解一个最优化问题？

存在很多方法来解每一种最优化问题。然而，介绍它们超过了这本书的范围。感兴趣的读者可以去看《优化模型和应用》Optimization Models and Application (El Ghaoui, 2015) 和 《凸函数优化》Convex Optimization (Boyd & Vandenberghe, 2004)，这两本好书即介绍了我们的主题又在网上可以免费阅读（查阅参照资料详细）。我们将焦点放回SVMs和掌握一个最优化问题使我们可以找到最优超平面。怎样去解SVMs最优化问题将在下一章详细介绍。

SVMs最优化问题

给出一个线性可分的训练集和一个由向量w和偏移量b定义的超平面，调用超平面的几何间隔M定义为：

这里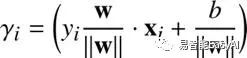是调用训练样例的几何间隔。

这个最优化的分类超平面就是用普通向量w和偏移量b定义的几何间隔最大的超平面。

找到w和b，我们需要解下面的最优化问题，约束条件为样例的间隔需要大于或等于M：

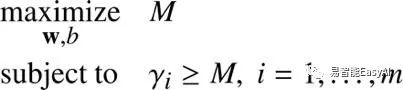
函数间隔和几何间隔的关系：

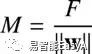
所以我们可以重写这个问题：

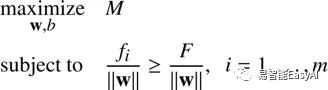
我们现在可以简化约束条件去掉不等式两边的范式：

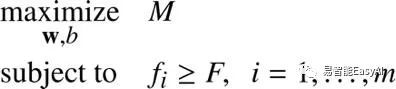
之前讲过我们试着去最大化几何间隔时等比改变W和b时不影响结果。我们可以选择等比变化的任意w和b，几何间隔不会变化。作为一个结果，我们决定等比改变W和b让F=1。它不会影响这个最优化问题。

问题就成了：

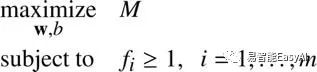
因为，所以问题等同于：

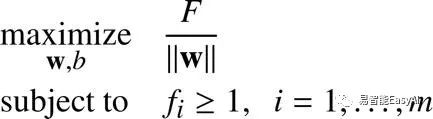
又因为我们决定让F=1，这就等价于：

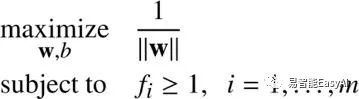
这个求最大值问题就等价于下面的求最小值问题：

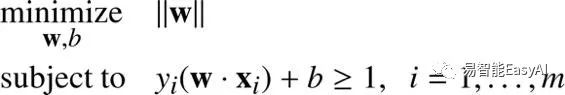
提示：你也可以从（https://www.svm-tutorial.com/2015/06/svm-understanding-math-part-3/）阅读最优化问题的替代推导，在那里我用函数间隔代替几何间隔。

下面的式子让这个最小化问题给出相同的结果。

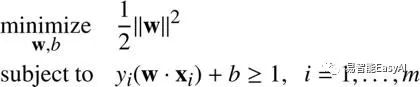
分式的增加是为了后来的方便，当我们用QP解法来解这个问题时范式的平方的优势在于去掉了求平方根。

最终，这个最优化问题在大部分的文献中写成：

为什么我们要费这么大的劲去重写这个问题？因为原始的最优化问题很难解，作为替代，我们现在有凸二次函数最优化问题，虽然它平淡无奇，但是非常容易解。

小结

首先，我们假定一些超平面要比其他的好：他它们要对未知的数据表现更好。在所有的超平面中，我们决定称其中最好的超平面为最优超平面。为了找到最优超平面，我们找到一个比较两个超平面的方法，而且最终因为一个数字可以让我们做到。我们意识到这个数字的几何意义且称它为几何间隔。

我们开始于最优超平面就是有最大几何间隔的超平面且我们可以用间隔的最大值去找到它。为了使事情简单化，我们注意到我们可以最小化w的范式，这个向量可以确定这个超平面，而且我们将确定w所确定的最优超平面（如果你回忆之前讲过的，会知道w是用在在计算几何向量的方程式中的）。