分类算法之支持向量机SVM

Posted 2021-04-26 机器学习学习机器

向劳动者致敬

被小长假耽误了更新，今天跟大家聊聊支持向量机。

支持向量机( Support Vector Machine)在上个世纪90年代就已经正式产生，在文本分类中显示出卓越性能。在90年代的机器学习领域，SVM是远超神经网路的神奇算法，并且它有完善的数学理论基础，涵盖凸优化，核函数，拉格朗日算子等。所以，即使在今天，支持向量机仍然有十分重要的地位。

0 1

分类问题

首先解释一下什么是分类问题。

举个例子来说，就像下面这张图，我们如何画一条完美的线将香蕉和苹果分开。

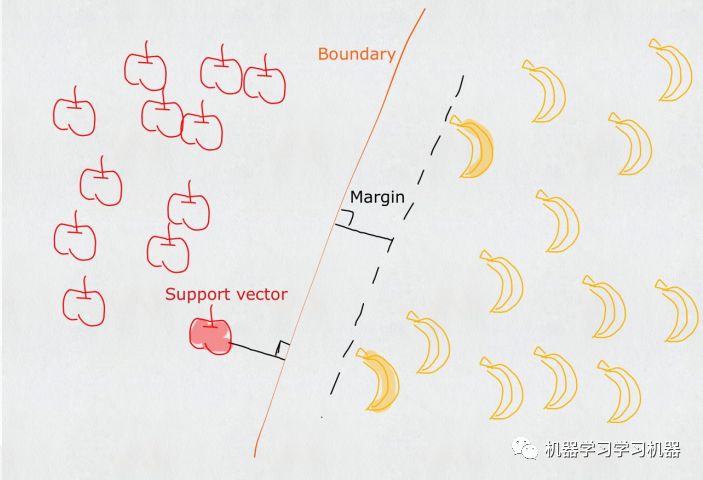
很好，这样的线可能有很多条。可是当香蕉和苹果更多的时候，你就会发现有一个香蕉和一个苹果站错了队，比如:

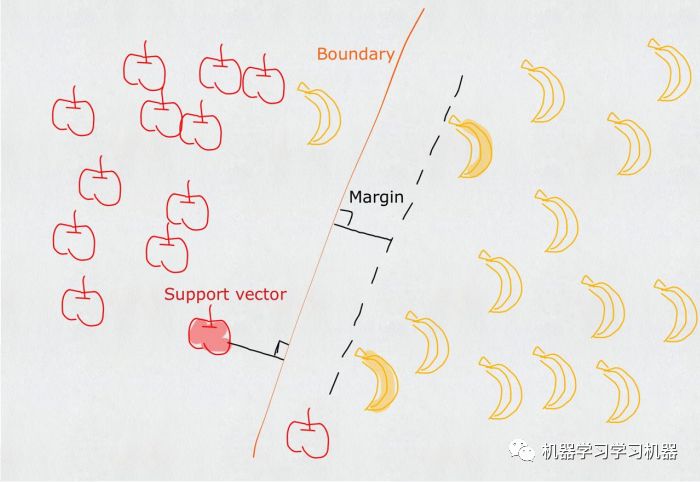
所以SVM所要解决的问题就是如何完美的将苹果和香蕉完美的分开，并且使它们之间的间隔尽可能的大。

0 2

支持向量机SVM

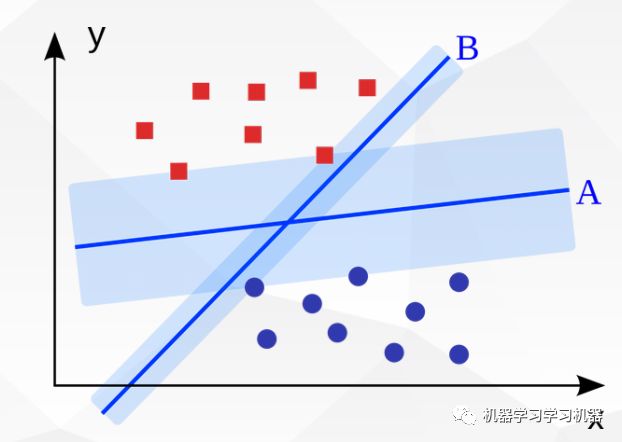
上图依然是一个分类问题，A和B都可以将红点和蓝点分开，但是哪个效果更好？

答案是A。因为从图上可以看出，不管是红点还是蓝点，边界点离直线A的距离都远大于B。对于分类器B来说，一旦有红点出现在A和B的位置，B就会犯错，而这个时候A依然是正确的。

所以支持向量机的核心思想就是：最大化间隔，最不受噪声的干扰。

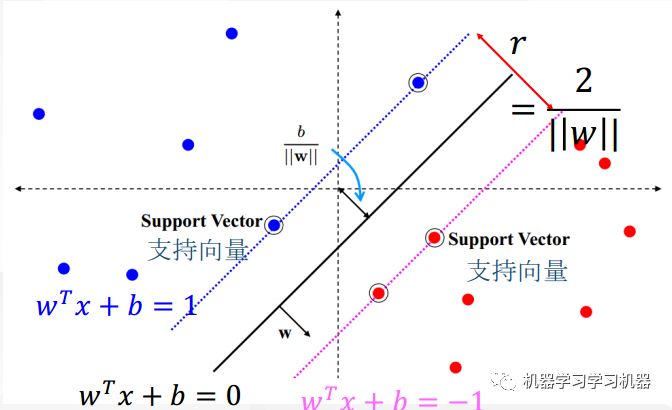
假设上面的问题是线性可分的，我们可以用一条黑线来划分蓝点和红点，那么位于红线和蓝线上的边界点就是“支持向量“，这两条线之间的间隔我们称之为"软间隔“()。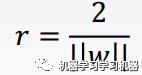

0 3

支持向量机的求解

将上面的问题表示成一个线性的公式就是：

y是我的目标变量，取值为-1和1，在线性等式满足使所有的y都正确分类的基础上，使得间隔 r 最大。 接下来就是一个线性约束的凸二次规划的问题，一定会有最优解。

在目前为止，我们都在讨论线性可分的情况，如果是像以下这种问题，你就会发现，你好像已经没有办法通过一条线把它分开了，这个时候怎么办呢？

我们很自然的就会想到，要是能把它转化为线性问题就好了。这个时候，核函数就出现了。我们通过某种变换，把一个二维的问题转化为三维问题，这样我们就可以通过一个平面去完美的画出这条线。当你把它映射到平面时，它就好像是一条曲线。

温馨提示

总的来说，支持向量机是分类算法的一种，通过支持向量的间隔最大化来解决分类问题，优化分类算法。当我们要解决的问题，线性可分时，SVM能够很方便的找出这条分类线。而对于线性不可分的问题，就需要通过核变化，将二维平面转换到三维甚至高维的空间去解决。

每天一点点，生活大不同。鼓励你们活蹦乱跳的给我留言，也欢迎大家点赞转发。

下期话题：分类问题之支持向量机SVM（二）