支持向量机（support vector machine, SVM）

Posted 2021-04-26 聪的2018迭代日记

支持向量的思想

给定一个样本集，分类学习最基本的想法就是基于训练集D在样本空间中找一个超平面，将不同类别的样本分开，但是能将训练样本分开的划分超平面可能有很多种。

划分超平面可以用以下方程描述：

ω为法向量，决定了超平面的方向，b为位移量。

样本中任意点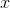到超平面的距离可以写为：

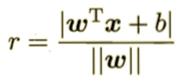
距离超平面最近的几个训练样本点使式子：

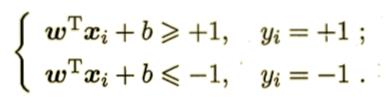
的等号成立。它们被称为“支持向量”（support vector）。距离为：

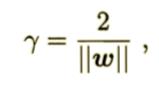
这个距离被称为“间隔”（margin）

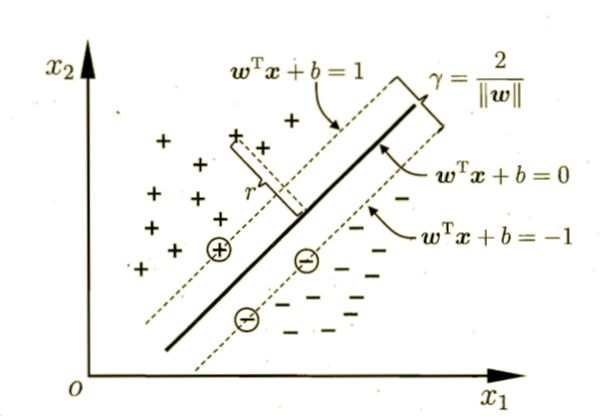
欲找到“最大间隔"的划分超平面，即为：

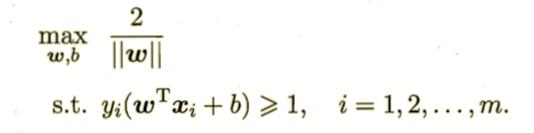
可以重写成：

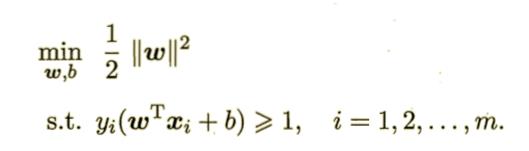
这就是支持向量机的基本模型。

对偶问题

我们求解这个最小值，可以使用一些优化计算包求解，但是还可以使用拉格朗日乘子法得到其“对偶问题”。

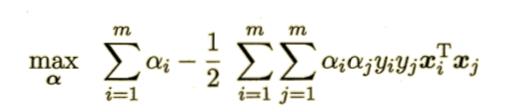
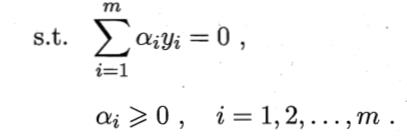
支持向量的一个重要性质就是，训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。

那么如何求解呢？这是一个二次规划的问题：这个问题的规模正比于训练样本数，这会在实际任务中找出很大的开销，为了避开这个障碍，人们提出了很多高效的算法，SMO是其中的一个代表。

核函数

在现实任务中，有很多样本空间是不能线性可分的，对这样的问题，可将样本从原始空间映射到一个高维空间。

另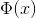表示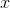映射后的特征向量，在特征空间中，超平面就是：

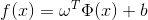
于是有：

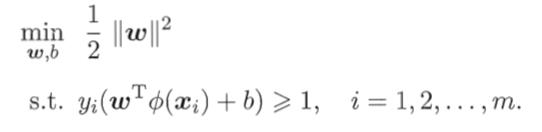
其对偶问题为：

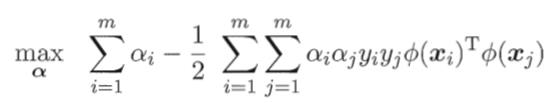
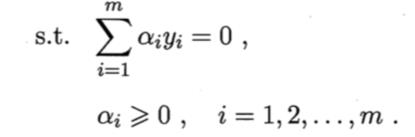
求解这个问题通常是非常困难的，因为涉及到一个问题，那就是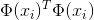：的求解非常困难，于是可以设想这样一个函数：

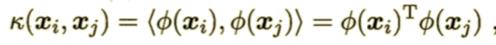
这个函数就是核函数。

于是对偶问题可以重写成：

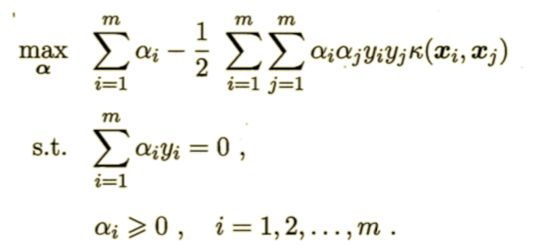
求解得到：

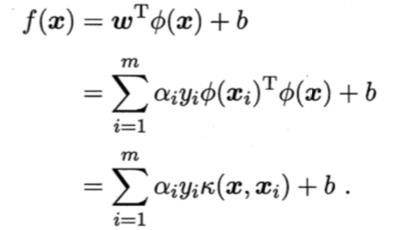
模型的最优解可以通过训练样本的核函数展开，这一展开式亦称为“支持向量展式”。

核函数的定义

只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。

软间隔与正则化

所有的样本都必须被超平面正确划分被称为“硬间隔”，而软间隔是允许某些样本不满足，如下图中的红色：

支持向量回归（SVR）

当且仅当预测函数与y之间有一个间隔带，落入其中的样本不计算损失，这样的回归模型就是支持向量回归。

核方法

通过引入核函数，将线性学习器扩展为非线性学习器。