好文力荐 | 从支持向量机到非平行支持向量机

Posted 2021-04-26 运筹千里

点击“运筹千里”关注

ORT & JORSC

从支持向量机到非平行支持向量机

邵元海, 杨凯丽, 刘明增, 王震, 

李春娜, 陈伟杰

本文通信作者介绍

邵元海

海南大学校聘教授，硕士生导师

摘要

非平行支持向量机是支持向量机的延伸, 受到了广泛的关注. 非平行支持向量机构造允许非平行的支撑超平面, 可以描述不同类别之间的数据分布差异, 从而适用于更广泛的问题. 然而, 对非平行支持向量机模型与支持向量机模型之间的关系研究较少, 且尚未有等价于标准支持向量机模型的非平行支持向量机模型. 从支持向量机出发, 构造出新的非平行支持向量机模型, 该模型不仅可以退化为标准支持向量机, 保留了支持向量机的稀疏性和核函数可扩展性. 同时, 可以描述不同类别之间的数据分布差异, 适用于更广泛的非平行结构数据等. 最后, 通过实验初步验证了所提模型的有效性.

关键词 数据挖掘, 支持向量机, 损失函数, 核学习, 非平行支持向量机

引言

非平行支持向量机作为支持向量机的拓展, 近几年受到了广泛的关注. 与支持向量机相比, 非平行支持向量机针对每一类别构造相应的支持超平面, 从而可以描述不同类别的数据分布差异, 对某些数据下的分类效果比支持向量机好, 比如交叉型数据等. 目前, 非平行支持向量机已经成为了支持向量机新的研究热点.

目前, 损失函数的研究是非平行支持向量机研究的热点之一. 然而关于支持向量机与非平行支持向量机之间的关系研究较少, 特别是至今没有一个非平行支持向量机可以退化或等价于标准的支持向量机模型. 本文正是从支持向量机出发, 研究非平行支持向量机. 利用构造不同的损失函数的特点, 提出能退化到标准支持向量机的非平行支持向量机模型和算法. 总结起来, 本文的主要贡献有:

i) 本文提出了一种新的非平行支持向量机模型, 该模型对分类问题引入了新的软间隔ε-不敏感损失函数, 并通过极小化ε-带宽度拟合每类样本类内的分布, 同时极大化类间分离的间隔, 适用于处理不同类型的数据.

ii) 本文提出的非平行支持向量机模型可退化为标准的支持向量机. 同时, 该模型保持了支持向量机的稀疏性和核函数可扩展性, 并且支持向量机的求解算法可以直接应用于该模型.

iii) 针对分离和拟合的情况, 本文给出了两种非平行支持向量机决策函数, 丰富了非平行支持向量机决策函数的意义.

iv) 最后, 本文从支持向量机角度出发研究非平行支持向量机, 丰富了支持向量机的内涵, 并为非平行支持向量机研究提供了一种新的研究思路.

提出的模型

前面提到的非平行支持向量机模型都能较好的处理交叉型等数据, 所使用的损失函数也各不相同, 但均不能退化为标准支持向量机模型. 本节我们从支持向量机出发, 研究非平行支持向量机. 注意到支持向量机中软间隔损失函数和ε-不敏感损失函数都有稀疏特性, 也是标准支持向量分类机和标准支持向量回归机所使用的损失函数. 我们从这两个损失函数入手, 构造一种新的损失函数并提出相应的非平行支持向量机模型.

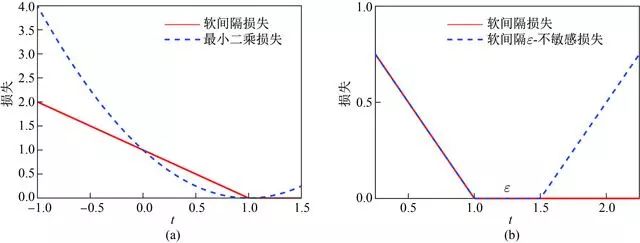
上图： (a) 支持向量机使用的软间隔损失和最小二乘损失函数  (b) 本文提出的软间隔ε-不敏感损失和软间隔损失函数

结论和展望

本文从支持向量机的特点出发, 通过定义新损失函数, 研究非平行支持向量机, 提出了一个新的非平行支持向量机模型. 该模型不仅可以退化为标准的支持向量机, 同时可以拟合样本点分布并最大化类间间隔, 也就是说该模型兼有支持向量机和拟合型非平行支持向量机的特点. 本文提出的非平行支持向量机模型具有稀疏性特性, 并且直接可用支持向量机算法求解. 我们通过实验验证了所提出的非平行支持向量机模型的有效性. 本文的研究为非平行支持向量机的研究提供了新的思路. 对于数据挖掘其他问题与模型, 如回归问题, 半监督问题和无监督问题等均可考虑构造与支持向量机等价的非平行支持向量机模型与算法. 而在推广的过程中, 如何控制新模型的复杂度和兼容性将是我们进一步工作的重点.

本文节选自：

邵元海, 杨凯丽, 刘明增, 等. 从支持向量机到非平行支持向量机 [J]. 运筹学学报, 2018, 22(2): 55-65.

小编

文章看累了，来看看作者吧

上图： 2017年邵元海(右)与恩师邓乃扬(左)

邵元海

教育经历

2008.9-2011.6  中国农业大学  管理学博士  

2006.9-2008.6  中国农业大学  理学硕士 

2002.9-2006.6   吉林大学         理学学士 

工作经历

2017.9至今  海南大学经济与管理学院  校聘教授  

2016.3-2017.3 University of California, Los Angeles   访问学者    

2016.1-2016.5  浙江工业大学之江学院   理学院执行院长    

2013.11-2016.6 浙江工业大学    硕士生导师    

2013.9-2016.6   浙江工业大学    副教授    

2012.7-2015.12 浙江工业大学之江学院   理学院院长助理    

2011.7-2013.9   浙江工业大学    讲师 

社会兼职

国家自然科学基金项目匿名评审专家

教育部学位中心通讯评议专家

中国统计学会理事

近期工作

主持的项目

1. 2018.1-2019.12 海南省自然科学基金项目: 大规模数据挖掘中稀疏问题的优化理论与算法(No.118QN181)   10 万  

2. 2017.9-2022.9   海南大学科研启动基金项目 ：基于统计学习理论的大数据分析 (No. kyqd(sk)1804)   160万 

近期论文

1. Shao Y H*, Li C N, Liu M Z, et al. Sparse Lq-norm least squares support vector machine with feature selection [J]. Pattern Recognition, 2018, 78: 167-181. 

2. Wang Z, Shao Y H*, Bai L, et al. Insensitive stochastic gradient twin support vector machines for large scale problems [J]. Information Sciences, 2018, 462: 114-131.

3.  Liu M Z, Shao Y H*, Wang Z, et al. Minimum deviation distribution machine for large scale regression [J]. Knowledge-Based Systems, 2018, 146: 167-180. 

4. 邵元海*, 杨凯丽, 刘明增,王震, 李春娜, 陈伟杰. 从支持向量机到非平行支持向量机 [J]. 运筹学学报, 2018 22(2): 55-65.

往期 精彩回顾

▼点击阅读原文，了解更多