这样一步一步推导支持向量机，谁还看不懂？

Posted 2021-04-26 Python与算法社区

后台回复 wuenda 获取鼻祖的最精简ML入门课, 回复 cs224 获取斯坦福NLP和深度学习的全部课程，回复数字 3 查看ML完整地由浅到深地学习笔记。

1 前言

讲解支持向量机(SVM)的文章数不胜数，不过大多缺乏中间很多推导细节。

相比其他经典机器学习算法，SVM里面有更多的数学推导，用到 拉格朗日乘子法 ， KKT条件 ，线性和非线性的 核函数 ，这些都对非数学专业的入门者造成一定门槛。

不过挑战意味着机遇，完全打通这些知识，可能会助你提升一个台阶，尽管当下SVM用的可能没有之前火爆，但SVM作为在深度学习模型之前应用最广泛的模型之一，仍然有必要研究推导，尤其是如果想继续深造，读博、做科研的。

昨天，闲来没事，又在纸上推导，纸笔学习体验效果一般。因此，今天试着在公式编辑器里感受下SVM的数学推导部分，用的方法比较直白，自信这个推导方法大家都能看明白。

SVM不再从头开始，直接从目标函数和约束部分开始，之前部分可以参考：

2 拉格朗日乘子法

OK. SVM经过拉格朗日乘子法，引入了 m 个系数，目标函数的形式如下：

变量含义和相关假设如下：

• 设 w 向量维度是 n,

  

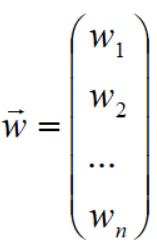
• a 的维度是 m (样本个数)，

• 样本(X,Y)的第一维度代表样本个数，设为m; 第二维度是特征维度n，如第 i 个样本的向量表示为：

  

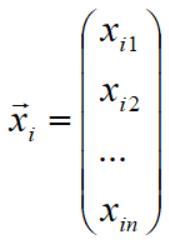
• b是标量

因此，下式可以化简为：

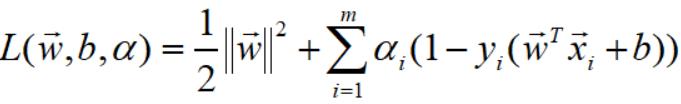
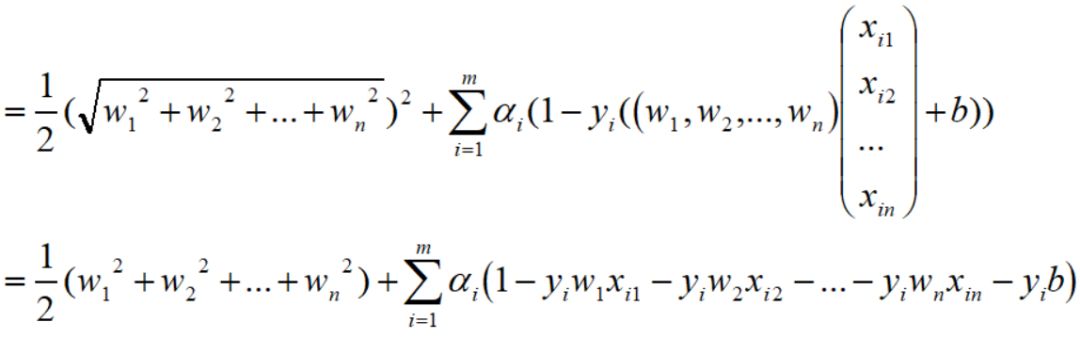
为了更好地理解， 先对w向量的第一个分量w1求偏导 ，和w1无关的分量全部消除，式子立即化简为如下：

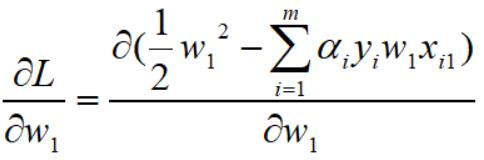
这些只涉及到最简单的求导公式，求出偏导：

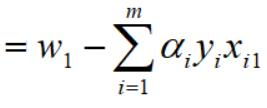
这样对w1的求导完毕，然后对整个的 w 向量求导：

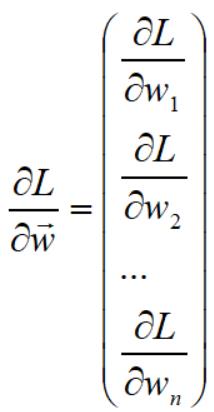
已经求得L对w1的偏导， w1,w2,…,wn的地位是相同的 ，所以依次带入即可，上式可以化简为如下：

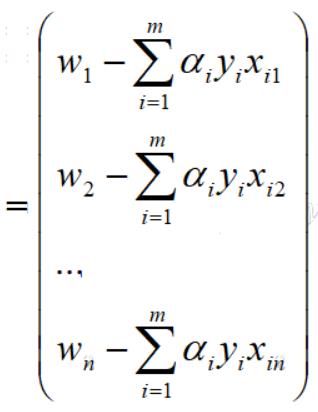
下面再利用一些基本的线性代数中行列式的一些知识，就可以转化为向量的表达，具体操作如下：

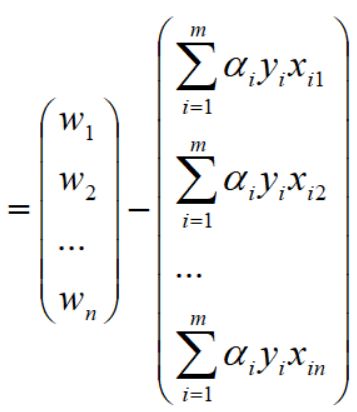
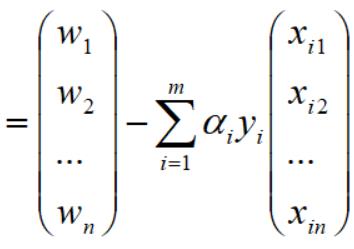
回到文章开始对w向量和xi向量的定义，得到如下向量表达：

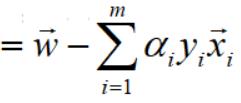
因此，对w向量的偏导求解完毕，结果如下：

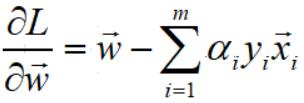
下面 再对b求导 ，b是标量，直接一步可以得到结果：

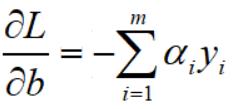
根据拉格朗日乘子法的理论，令L对w偏导等于0，得到关系式：

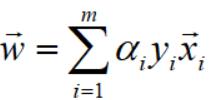
同理，令L对b偏导等于0，得到关系式：

3 化简L

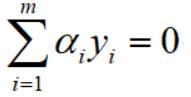
接下来，将得到2个关系式代入到L中，化简L.

为了更好理解，仍然采用更直观地表达方式，将向量完全展开，

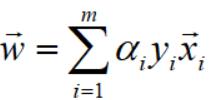
将上面关系式代入到L之前，我们先展开这个式子，

仍然还是先抽出w的第一个分量w1，因为L完全展开中涉及到其平方，

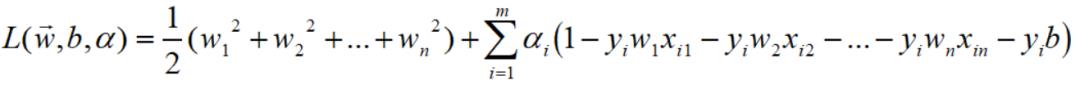
所以， 先化简w1的平方这一步 。因为w1可以进一步展开成如下形式：

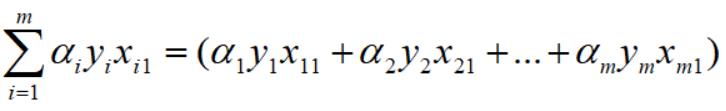
w1的平方，因此可以展成如下形式：

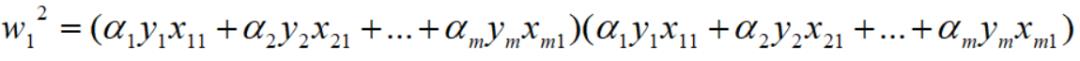
上面这个式子就是基本的多项式求和，w1的平方进一步浓缩下：

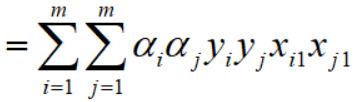
至此，w1的平法化简完毕，再整合所有其他w分量并求和，如下，整个推导过程依然相清晰，如下：

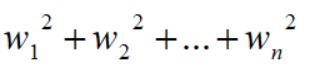
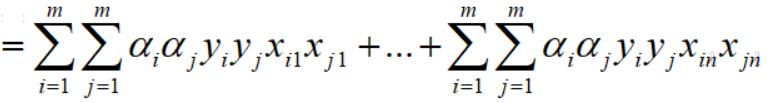
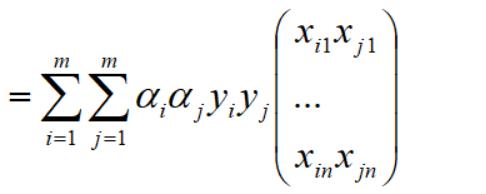
再对上式拆分成两个向量，如下：

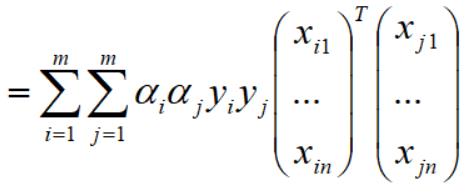
再写成浓缩式子：

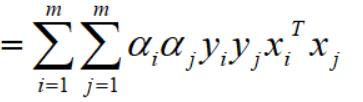
至此，代入w后化简中的第一项已经完毕。

再化简第二块：

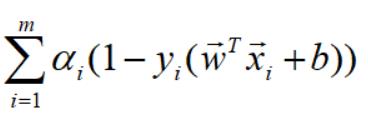
对上式展开，并利用条件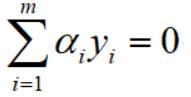：，化简如下：

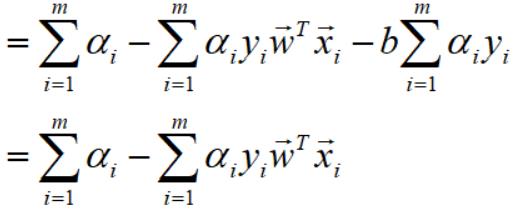
代入w满足的等式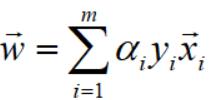后，

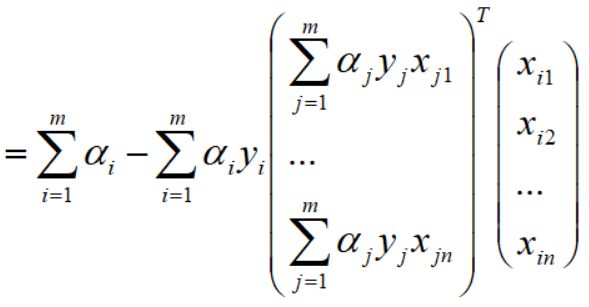
提取出公因子后变为如下：

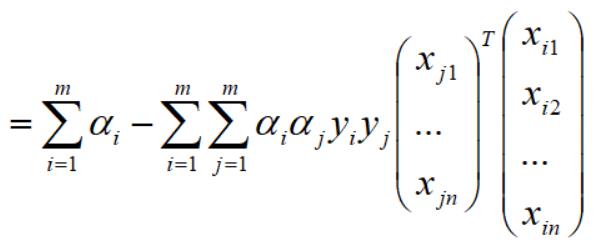
将上式写为向量形式：

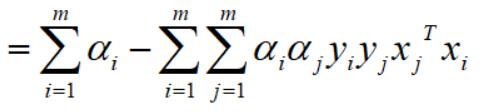
因为都是向量，所以转置相等，故，

至此，第一二项求解完毕，整理后得到：

4 小结

OK. 经过一番折腾，目标函数终于变为只有一个系数的函数，限于篇幅，接下来详细推送KKT求解全过程，敬请关注。

文章用心血凝聚，不走捷径，如不反感可否<点广告点赞>支持下， 这样我会更加坚定初心，更有勇气在这条"与别人不一样"的艰辛原创之路上一直走下去 …