监督学习——支持向量机(Support Vector Machine)
Posted 统计学习与PyR
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了监督学习——支持向量机(Support Vector Machine)相关的知识,希望对你有一定的参考价值。
昨天讲了核函数在SVM中的应用,今天我们谈谈数据不可分的情况以及SMO算法。
1.正则化和不可分情况(Regularization and the non-separable case)
截止目前,我们对SVM进行的推导,都有一个假设,就是样本数据是线性可分的,当样本数据线性不可分时,我们虽可以通过核函数将特征映射到高维特征空间中,这样会增加样本数据可分的概率,但并不是一定可以保证样本数据可分。比如说在某些案例中,我们找到的分类超平面不一定是所我们想要的,因为有的时候样本数据可能会出现异常值的情况。比如我们看下面左图所示的,是一个最优间隔分类器,但是如果有一个单独的异常值落在了右上方的区域,如下面右图所示,这样就会导致分界线出现明显的偏移,还会导致分类器的间隔缩小很多。
因此,我们可以看出之前的模型对噪声是非常敏感的,并且这里如果异常值在另外一个类中,这时候就是线性不可分啦。
这时候,要想让SVM算法能够适用于非线性可分的数据集,并且对异常值不太敏感,那么就需要对之前的优化模型进行重新构造(利用L1正则化),如下所示:
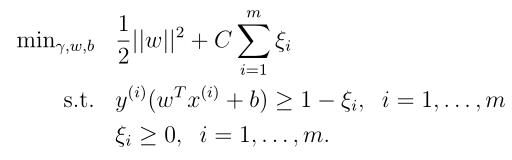
其中非负参数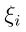 称为松弛变量,有了这个参数后,某些样本点的函数间隔就可能小于1啦,也就是说这些样本点都在最大间隔区间里面。由于我们放松了约束条件,所以需要重新调整目标函数,以对异常值进行惩罚,也就是在目标函数后面加上
称为松弛变量,有了这个参数后,某些样本点的函数间隔就可能小于1啦,也就是说这些样本点都在最大间隔区间里面。由于我们放松了约束条件,所以需要重新调整目标函数,以对异常值进行惩罚,也就是在目标函数后面加上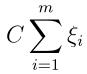 ,其中C表示惩罚因子,也就是异常值的权重,这就表明异常值越多,目标函数值会越大,而我们需要尽可能小的目标函数值。C越大表明异常值对目标函数影响越大,就是说我们越不希望看到异常值,并且我们可以看出目标函数控制了异常值的数目和程度,使大部分样本点仍然遵守约束条件,即大部分样本点都有至少为1的函数间隔。
,其中C表示惩罚因子,也就是异常值的权重,这就表明异常值越多,目标函数值会越大,而我们需要尽可能小的目标函数值。C越大表明异常值对目标函数影响越大,就是说我们越不希望看到异常值,并且我们可以看出目标函数控制了异常值的数目和程度,使大部分样本点仍然遵守约束条件,即大部分样本点都有至少为1的函数间隔。
模型修改后,我们的拉格朗日函数修改为:
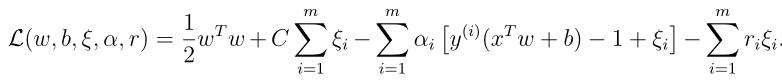
其中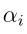 和
和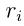 都是拉格朗日乘数,并且都大于等于0。
都是拉格朗日乘数,并且都大于等于0。
下面我们就不再对其对偶问题进行详细推导啦,和之前一样哈,先写出拉格朗日函数,然后将其看作是变量 w 和 b 的函数,分别对其求偏导,得到 w 和 b 的表达式。然后代入公式中,求带入后公式的最大值。整个推导过程类似之前的模型,下面写出最后的结果如下:
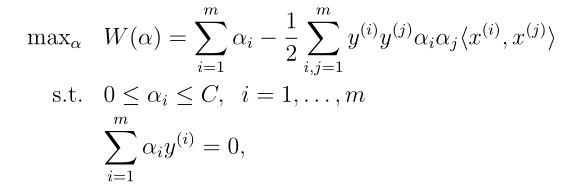
跟之前一样,我们可以把w用αi 来进行表述,如同等式(9)所示,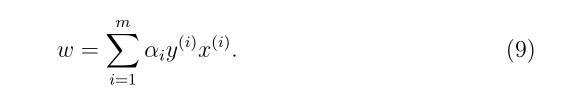
所以解决对偶问题之后,接下来我们就可以使用等式(13)来进行预测啦。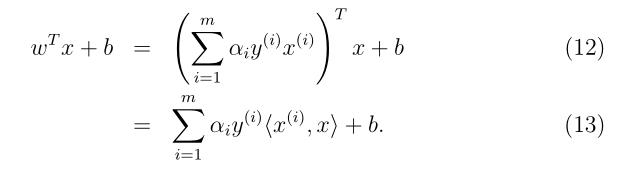
注:你有没有发现在进行L1正则化之后,唯一改变的是对偶问题的约束条件从原来的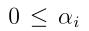 变成了现在的
变成了现在的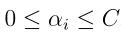 。这里
。这里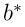 的计算也受到了影响而发生改变,也就是说之前的等式(11)不再成立啦,具体等于多少,后续再补充。
的计算也受到了影响而发生改变,也就是说之前的等式(11)不再成立啦,具体等于多少,后续再补充。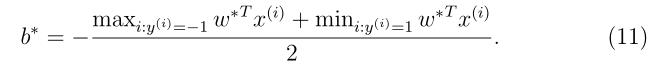
另外,此时的KKT对偶互补条件变为:
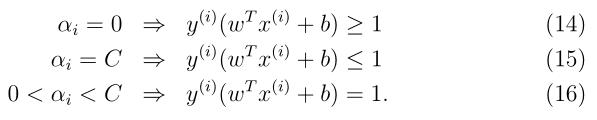
式子(14)表明在两条间隔线外的样本点前面的系数为0,式子(15)表明异常样本点前面的系数为C,式子(16)表明支持向量(即在分类超平面两边的最大间隔线上的样本点)前面的系数在0到C之间。所以通过KKT对偶互补条件可知,在最大间隔线上的某些样本点可能也不是支持向量,可能是异常值。
现在,剩下的问题就是给出一个算法来具体地解之前以及现在给出的对偶问题啦。
2.SMO(Sequential Minimal Optimization)算法
SMO算法叫做序列最小最优化算法,对于解决由SVM推导出的对偶问题,这一算法提供了一种有效的解法。我们先讲讲坐标上升算法(coordinate ascent algorithm),这是用来推导SMO优化算法中的一步。
2.1 坐标上升算法(Coordinate ascent)
假如我们要解决下面这样的无约束优化问题:
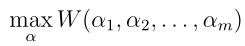
这里的W是关于参数αi的某种函数,和SVM算法没有任何关系。我们在前面讲回归的时候学过了两种优化算法:梯度下降法和牛顿法。下面我们来讲一个新的优化算法——坐标上升法(在求解最小值问题时,称为坐标下降法,原理一样哈):
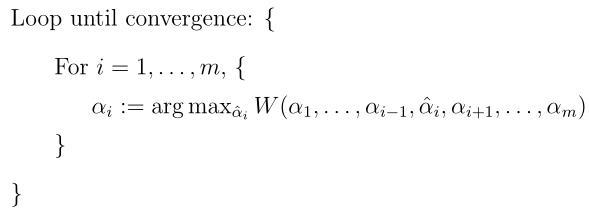
在算法最内层的循环中,给定除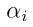 之外的所有的
之外的所有的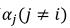 ,此时W可看作是关于
,此时W可看作是关于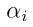 的函数,所以直接对
的函数,所以直接对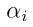 进行求导进行取最大优化就行了。这里我们对变量进行最大化求导的顺序为i从1到m,当然也可以改变优化顺序来使得W能快速地增加并收敛。如果W在最内层的循环中能够快速地达到最优,此时坐标上升法便是一个求极值的高效方法。下面是坐标上升算法的一个示意图:
进行求导进行取最大优化就行了。这里我们对变量进行最大化求导的顺序为i从1到m,当然也可以改变优化顺序来使得W能快速地增加并收敛。如果W在最内层的循环中能够快速地达到最优,此时坐标上升法便是一个求极值的高效方法。下面是坐标上升算法的一个示意图:
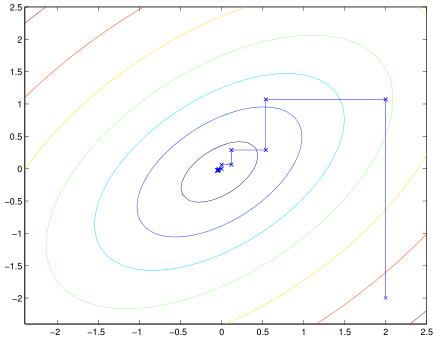
上图中的椭圆形就是我们要进行优化的二次函数的轮廓线。也就是说变量为2个。这里设置坐标上升法的初始值为(2,−2),图中标出了此算法求解全局最大值所经过的路径。同时在坐标上升法的每一步,其移动的方向都是平行于坐标轴的,这是因为每一步只对一个变量进行优化。
2.2 SMO算法(简单了解下)
SMO算法对于线性SVM和数据稀疏时性能很好。我们利用这个算法解决之前留下的对偶问题:
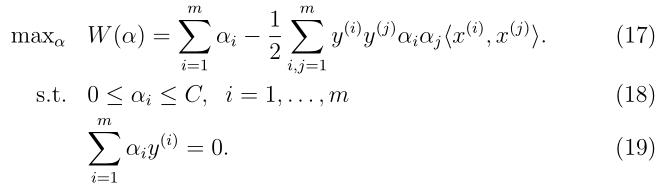
假设有满足约束条件(18-19)的αi构成的集合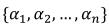 。假设我们固定
。假设我们固定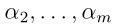 的值,然后进行一步坐标上升,重新优化对应α1的目标值,但是不幸的是这样解不出来,因为约束条件(19)表明:
的值,然后进行一步坐标上升,重新优化对应α1的目标值,但是不幸的是这样解不出来,因为约束条件(19)表明:
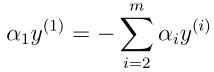
对上面的式子两边同乘以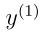 ,这个式子便等价于:
,这个式子便等价于:
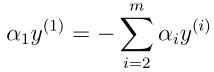
注:左边也乘以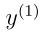 后,会出现
后,会出现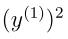 ,由于
,由于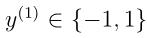 ,所以
,所以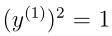 。
。
从上面的式子我们可以看出,α1是由其他的αi决定的,所以如果我们固定 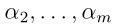 的值,那么就没办法对α1的值进行更新,如要更新就会不满足优化问题中的约束条件(19)啦。
的值,那么就没办法对α1的值进行更新,如要更新就会不满足优化问题中的约束条件(19)啦。
因此,如果我们要对αi中的一些值进行更新的话,就必须至少同时更新两个,这样才能保证满足约束条件。基于这个情况就衍生出了SMO 算法,算法过程如下所示:

意思就是,选择某一对αi和αj以在下次迭代中进行更新(这里需要选择那种能朝全局最大值方向最大程度靠近的一对值,有种方法叫做启发式方法:主要思想是在每次选择拉格朗日乘数的时候,优先选择样本前面系数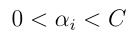 的αi作优化,因为在边界上的样本点(αi为0或C)对应的系数αi一般不会更改),然后使用对应的αi和αj来重新优化W(α) ,而固定其他的
的αi作优化,因为在边界上的样本点(αi为0或C)对应的系数αi一般不会更改),然后使用对应的αi和αj来重新优化W(α) ,而固定其他的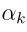 值,其中
值,其中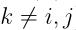 ,重复上面的过程直到收敛为止。
,重复上面的过程直到收敛为止。
注:我们可以检查在某些收敛公差参数 tol 范围内,KKT 对偶互补条件能否被满足,以此来检验这个算法的收敛性。这里的tol是收敛公差参数(convergence tolerance parameter),通常设定为0.01到0.001。
下面我们就简单的推导下上面的算法的大概思路。
我们依旧假设有满足约束条件(18-19)的αi构成的集合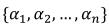 ,此时如果我们固定
,此时如果我们固定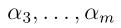 值,然后使用α1和α2来重新优化
值,然后使用α1和α2来重新优化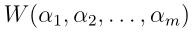 ,这样成对的更新也就满足了约束条件。根据约束条件(19),可以得到:
,这样成对的更新也就满足了约束条件。根据约束条件(19),可以得到:
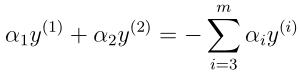
由于等号右边的值是固定的,所以将其写成一个常数ζ,即:

所以我们可以用下面的图来表达α1和α2所满足的约束条件:
由约束条件(18)可知,α1和α2在[0,C]×[0,C]正方形区域内,在此区域内有条直线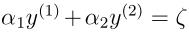 ,α1和α2在这条直线上。由通过上面的约束条件,我们还可以知道L≤α2≤H,否则(α1,α2)就不能同时满足在正方形区域内并位于直线上这两个约束条件了。我们利用等式(20),还可以把α1写成α2的函数形式:
,α1和α2在这条直线上。由通过上面的约束条件,我们还可以知道L≤α2≤H,否则(α1,α2)就不能同时满足在正方形区域内并位于直线上这两个约束条件了。我们利用等式(20),还可以把α1写成α2的函数形式:
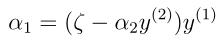
具体怎么来的自己算下,很简单的(用到了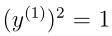 )。
)。
所以目标函数W(α)就可以写成:
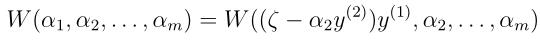
其中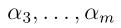 为常数,所以上面这个函数其实只是关于α2的一个二次函数。因此可以写成
为常数,所以上面这个函数其实只是关于α2的一个二次函数。因此可以写成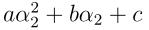 的形式,其中a,b,c为已知参数。此时对W进行求导并令为0便可以得到点α2,记为
的形式,其中a,b,c为已知参数。此时对W进行求导并令为0便可以得到点α2,记为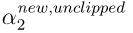 。但是要在L≤α2≤H范围内取得最大值,所以有:
。但是要在L≤α2≤H范围内取得最大值,所以有:
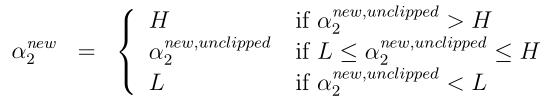
最终,我们得到之后,利用等式(20)就能得到的最优值啦。
关于如何在SMO算法运行的同时来对b进行更新,这里就不说啦,想了解的可以看看John C. Platt的资料《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》。
到此关于SVM的一些基本问题就讲完了,其实还有不少问题没叙述,比如多分类问题等。
总结下:对于了解SVM算法,需要知道函数间隔和几何间隔,还有凸优化的一些基础知识。然后我们主要解决的是三种问题:
线性可分支持向量机:硬间隔最大化——硬间隔支持向量机
线性支持向量机:软间隔最大化——软间隔支持向量机
非线性支持向量机:核函数
以上是关于监督学习——支持向量机(Support Vector Machine)的主要内容,如果未能解决你的问题,请参考以下文章