机器学习简单实践——支持向量机

Posted 2021-04-26 数据皮皮侠

本期导读	机器学习简单实践——支持向量机	Oct.17 2019
01	概念
02	特点
03	应用
04	线性分类器
05	实践模块

 

1 概念

在机器学习中，支持向量机（英语：support vector machine，常简称为SVM）是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。类似于逻辑回归，这个模型也是基于线性函数wTx+b的。不同于逻辑回归的是，支持向量机不输出概率，只输出类别。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

除了进行线性分类之外，SVM还可以使用所谓的核技巧有效地进行非线性分类，将其输入隐式映射到高维特征空间中。

2 特点

输入样本后将分类器的结果与1/-1比较，大于1或小于-1可确定类属，介于两者之间则不予分类。

通过最大化几何间隔来训练分类器，只有支持向量会进行参数模型训练。

对于线性不可分的样本通过映射到高维空间来实现线性可分，这个映射关系不好确定，核函数则很巧妙的解决了这个问题，也正是因为核函数的引入，svm有效的克服了维度之咒。为了克服少量离群点的干扰可在模型中加入松弛变量和惩罚因子，对于分布不均的样本，可通过惩罚因子来进行调节。每个样本都有一个松弛变量而惩罚因子则是固定的，需要由用户输入(核函数的参数也需要用户输入，这里就涉及一个参数寻优的问题)。

3 应用

用于文本和超文本的分类，在归纳和直推方法中都可以显著减少所需要的有类标的样本数。

用于图像分类。实验结果显示：在经过三到四轮相关反馈之后，比起传统的查询优化方案，支持向量机能够获取明显更高的搜索准确度。这同样也适用于图像分割系统。

用于手写字体识别。

用于医学中分类蛋白质，超过90%的化合物能够被正确分类。基于支持向量机权重的置换测试已被建议作为一种机制，用于解释的支持向量机模型。支持向量机权重也被用来解释过去的SVM模型。为识别模型用于进行预测的特征而对支持向量机模型做出事后解释是在生物科学中具有特殊意义的相对较新的研究领域。

4 线性分类器

首先给出一个非常非常简单的分类问题（线性可分），我们要用一条直线，将下图中黑色的点和白色的点分开，很显然，图上的这条直线就是我们要求的直线之一（可以有无数条这样的直线）

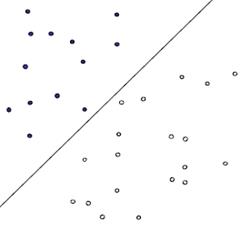
假如说，我们令黑色的点 = -1， 白色的点 = +1，直线f(x) = w*x + b，这儿的x、w是向量，其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候，f(x) 表示二维空间中的一条直线。

我们令黑色白色两类的点分别为+1, -1，所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。但是，我们怎样才能取得一个最优的划分直线f(x)呢？这有两种直线划分的分法。

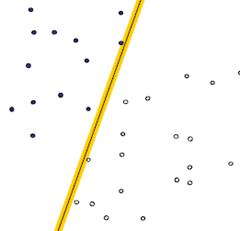
第一种分法

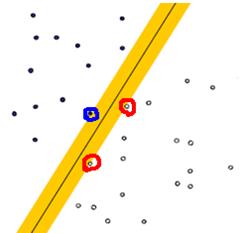
第二种分法

上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。

这两种分法哪种更好呢？从直观上来说，就是分割的间隙越大越好，把两个类别的点分得越开越好。在SVM中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是有很多道理的，比如说从概率的角度上来说，就是使得置信度最小的点置信度最大。

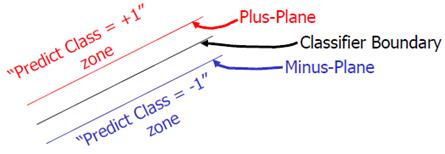
上图就是一个对前面说的类别中的间隙的一个描述。Classifier Boundary就是f(x)，红色和蓝色的线（plus plane与minus plane）就是support vector所在的面，红色、蓝色线之间的间隙就是我们要最大化的分类间的间隙。

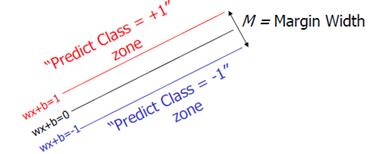
这里直接给出M的式子：

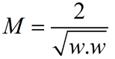
另外支持向量位于wx + b = 1与wx + b = -1的直线上，我们在前面乘上一个该点所属的类别y，就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单的将支持向量表示出来了。当支持向量确定下来的时候，分割函数就确定下来了，两个问题是等价的。之后我们可以优化求解，最终通过拉格朗日等数学方法得到线性可分问题的优化式子。

5 实践模块

5.1问题背景

我们继续使用之前推送中用过的数据集——鸢尾花，其中包含花瓣的长度和宽度，花萼的长度和宽度的数据。在scikit-learn的datasets模块中，我们可以调用load_iris函数，载入iris数据集。

5.2实践代码

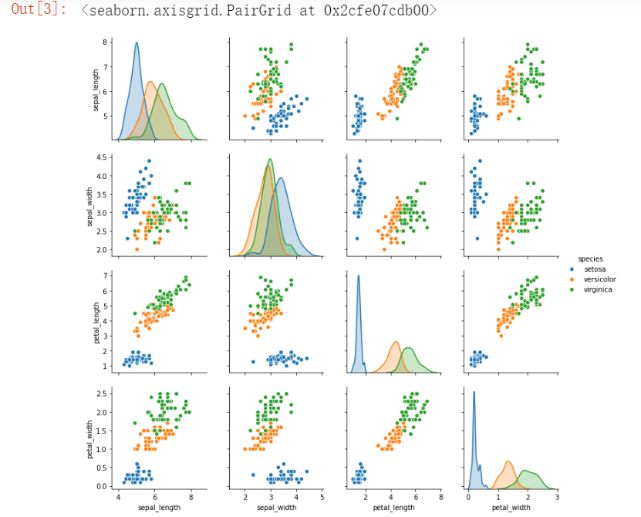
# 导入数据import seaborn as snsiris = sns.load_dataset('iris')iris.head()
# 探索性数据分析（EDA）import pandas as pdimport numpy as npimport matplotlib.pyplot as plt%matplotlib inlinesns.pairplot(iris, hue='species')

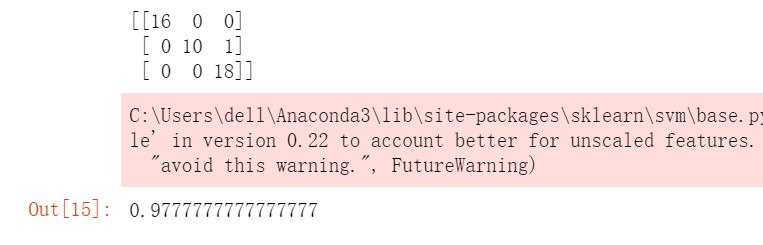
svm.fit(X_train,y_train)
# 模型评估pred = svm.predict(X_test)# 划分训练集与测试集from sklearn.model_selection import train_test_split
X = iris.drop('species', axis = 1)
y = iris['species']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.30，random_state = 100)
# 训练SVC模型
from sklearn.svm import SVC
svm = SVC()
from sklearn.metrics import classification_report,confusion_matrixprint (confusion_matrix(y_test, pred))svm.score(X_test, y_test)

运行结果如下：

以上就是全部内容啦，希望能对大家有帮助，更好地了解机器学习里的支持向量机的算法。

本期编辑校对：李嘉楠

长按关注“ 数据皮皮虾 ”

更多知识等你发现