线性不可分支持向量机：机智的核技巧

Posted 2021-04-26 AI派

点击上方“ AI派”，选择“ 设为星标”

最新分享，第一时间送达！

本文是《机器学习宝典》第 10 篇，读完本文你能够掌握机器学习中线性不可分支持向量机模型。

在前一篇 中已经知道通过支持向量能够找到一个超平面，将两类样本正确划分。但是实际生活中，原始的样本空间中可能并不存在这样的超平面将两类样本正确划分，也就是线性不可分，支持向量机通过将原始特征空间映射到高维特征空间来解决样本线性不可分的情况。

从线性不可分到线性可分

实际上，如果样本的原始特征空间是有限维，即特征个数有限，虽然样本有可能在原始空间中线性不可分，但一定存在一个高维空间使得样本可分。

令 表示将样本 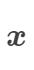映射到高维的特征向量，那么在特征空间中划分超平面所对应的模型可表示为：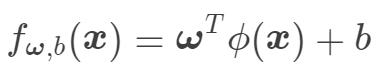

则支持向量机的基本型可以表示为：

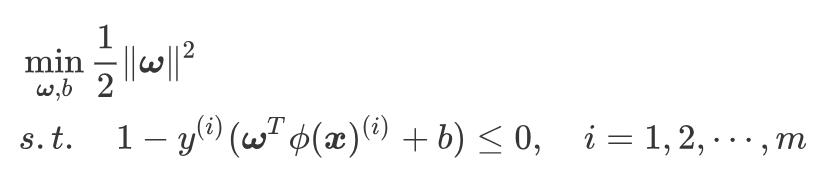
对偶型可以表示为：

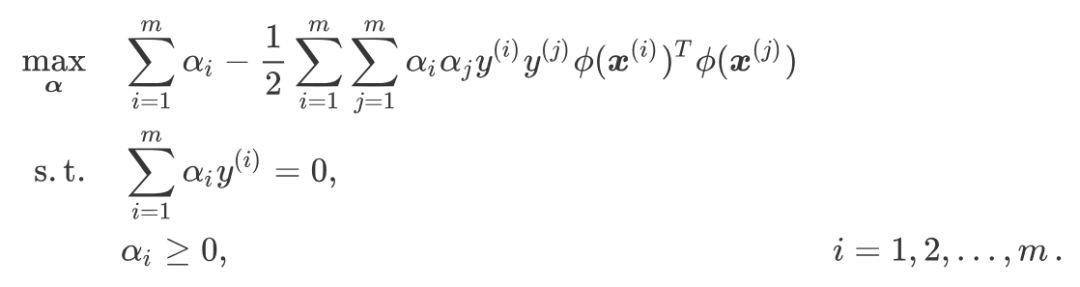
核技巧

从前面的对偶问题可以看到，在计算时会涉及到 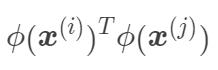，这表示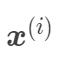样本 和样本 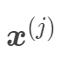映射到高维特征空间之后的內积，由于映射后的维度可能非常高，甚至可能无穷维，因此直接计算 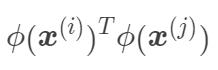的成本会非常高。

为了解决这个问题，引入了核技巧（kernel trick）。核技巧希望构造一个核函数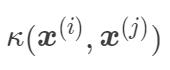，使得：

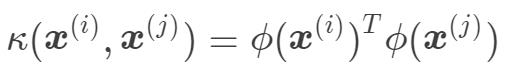
也就是说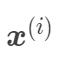， 样本 和样本 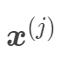在高维特征空间的內积等于它们在原始低维空间中通过函数 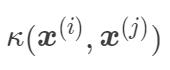计算的结果，这样就避免了维度灾难问题。

核函数的选择

既然通过核技巧能够解决特征映射到高维后计算量过大的问题，但面对一个现实任务, 我们很难知道应该具体向什么样的高维空间映射, 即应该选什么样的核函数, 而核函数选择的适合与否直接决定整体的性能 。

通过 Mercer定理 可以得到核函数的充分必要条件，这里我们不做深入介绍，只是列举一些常见的核函数。

线性（Linear）核函数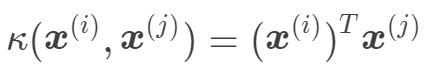

线性核函数其实就是前面介绍的线性可分的情况下的支持向量机。

多项式（Polynomial ）核函数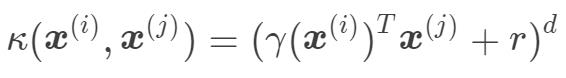
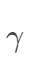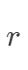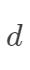其中，，， 都需要自己设定。

高斯（Gaussian ）核函数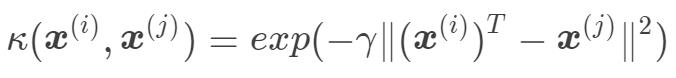

其中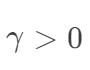，，需要自己设定。高斯核函数也叫径向基核函数（Radial Basis Function，RBF）。

Sigmoid核函数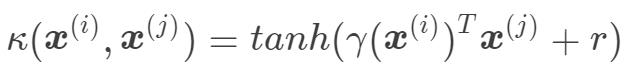

其中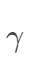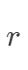，， 都需要自己设定。

通常，当特征维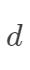数 超过样本数 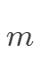时 (文本分类问题通常是这种情况)， 使用线性核； 当特征维数 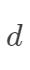比较小。样本数 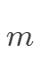中等时, 使用 RBF 核； 当特征维数 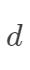比较小，样本数 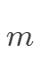特别大时,支持向量机性能通常不如深度神经网络 。

当然了，还可以通过函数组合得到核函数。如果 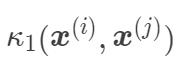和 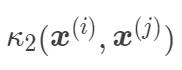  是核函数，那么下面的函数也是核函数：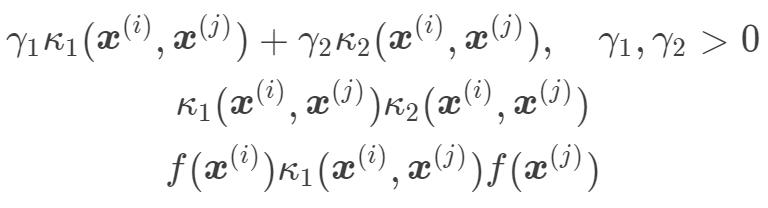

有了核函数之后，我们求解对偶问题的解，可以得到线性不可分的支持向量机的解的形式如下：

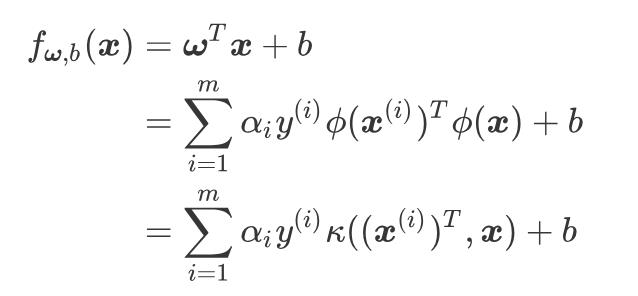
可以看到，加入了核函数之后的支持向量机形式其实与未加入之前整体形式上还是保持一致的。

参考：

1. 周志华.机器学习.第六章（支持向量机）

2. 深入浅出ML之Kernel-Based家族

   (http://www.52caml.com/head_first_ml/ml-chapter4-kernel-based-family/)

3. 从零推导支持向量机(SVM)

   (https://zhuanlan.zhihu.com/p/31652569)

4. 支持向量机通俗导论（理解SVM的三层境界）

   (https://blog.csdn.net/v_JULY_v/article/details/7624837)

   
   

（完）

---

---

最后说件事，我开通了知识星球，在星球里会分享我个人在数据分析/机器学习/深度学习/推荐系统方面的所学和所得。当前正在星球里分享我录制的机器学习视频课，如果想快速入门和提高自己，可以加入我的星球来交流（加入方式：扫描下方二维码或者点击“阅读原文”）。当前加入还可直接返现19.20元。

历史推荐

 | 

 

长按，识别二维码，加关注