支持向量机软间隔：有时候错误并非一定是坏事

Posted 2021-04-26 AI派

本文是《机器学习宝典》第 11 篇，读完本文你能够掌握机器学习中支持向量机的软间隔问题。

在 和 中我们已经学到了如何通过支持向量机去处理线性可分与线性不可分的问题，这篇文章我们来看下另外一个问题：软间隔（soft margin）。软间隔的目的其实就是通过容忍一些错误（离群点）分类的方式来获得更好的泛化性能。

软间隔

虽然通过核函数可以解决线性不可分的问题，但在实际任务中，很难找到合适的核函数去使得样本线性可分；其次，即便找到这样的核函数使得线性可分，但可能会使得模型过拟合，因此我们放宽对模型的要求，即允许模型对少量样本分类错误。

解决该问题的一个办法是引入软间隔的概念，如图所示：

也就是说，前面我们提到的支持向量机都属于“硬间隔”，也就是要求所有的样本都分类正确，现在我们希望在优化间隔时, 允许分类错误的样本出现, 但这类样本应尽可能少，这些分类错误的样本不满足约束条件 。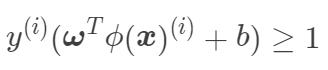

这样，我们的原始问题的优化目标可以写为：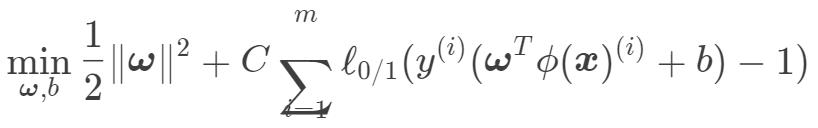

其中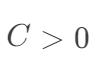， 是一个常数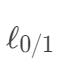， 是“0/1损失函数”

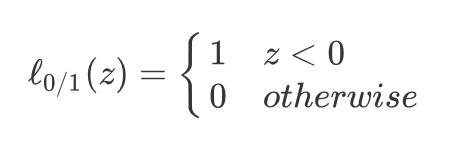
损失函数

上面已经得到了软间隔支持向量机的目标函数，然而，由于 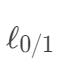 非凸、非连续，数学性质不好，人们通常使用其他的函数来替代它，这些函数是 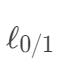的上界，即都是大于等于 0 的。下面给出几个常见的替代函数。

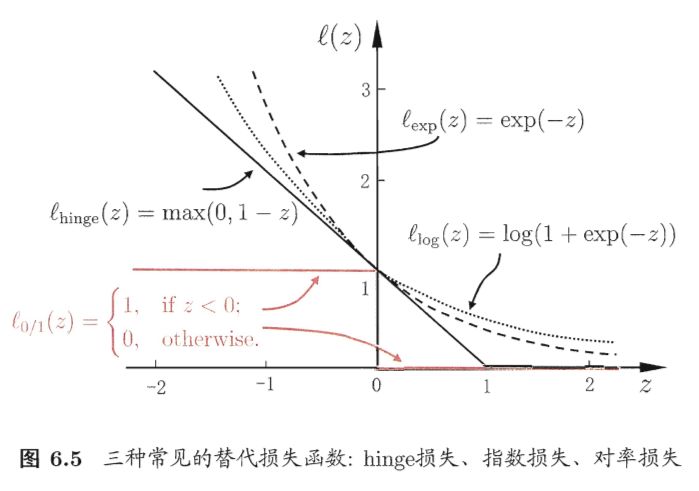
hinge损失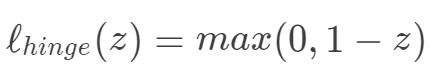

指数损失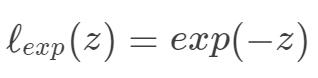

对率损失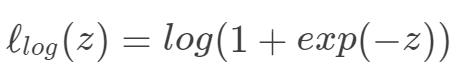

如果采用 hinge 损失，则优化目标可以转为：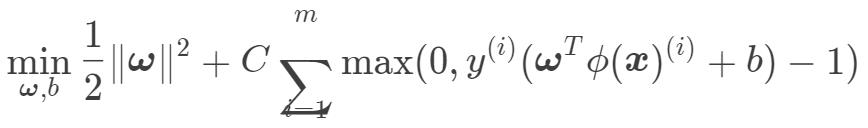

惩罚因子与松弛变量

前面提到了 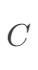是一个大于 0 的常数，这里再介绍一下 C 的另外一个名字：惩罚因子，为什么叫惩罚因子呢？因为 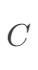的大小可以表示对离群点分错的重视程度，当 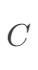趋于无穷大时，会尽可能使得 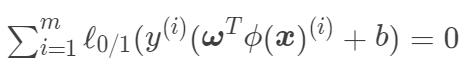，也就是所有的样本均满足约束条件 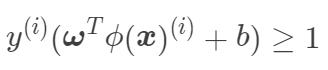，这时就退化成了硬间隔分类器。换句话说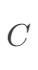， 越大，越希望所有的样本都能够正确分类。

这里我们引入松弛变量 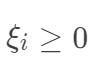，则将软间隔支持向量机要优化的问题重写为：

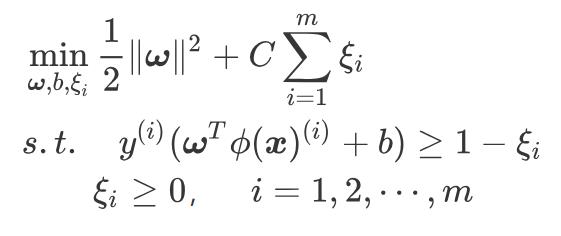
可以看到，松弛变量 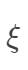表示对离群点分错的容忍程度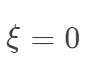， 时表示不能容忍离群点分错，也就是希望所有的样本都能够正确分类。

软间隔支持向量机的对偶问题

通过拉格朗日法可以求出上面式子的拉格朗日函数：

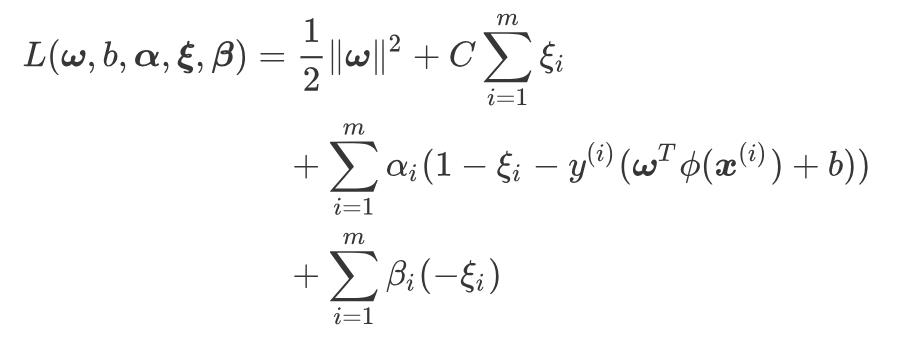
其中，，。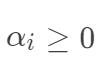

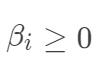这样软间隔的支持向量机要优化的问题可以等价于：

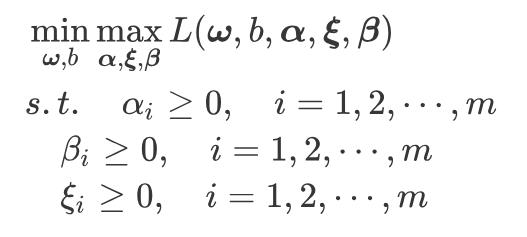
上面便是原问题，对应的对偶问题如下：

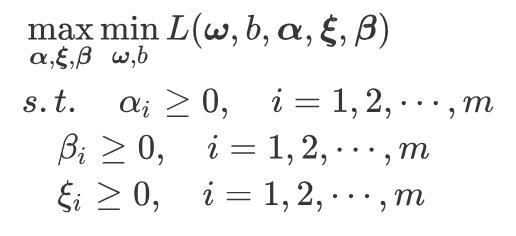
然后令 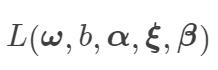分别对 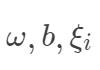的偏导为 0，得：

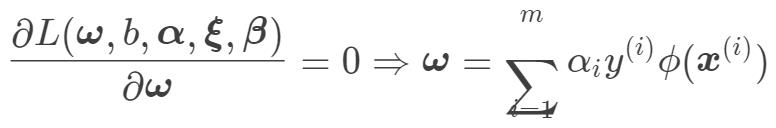
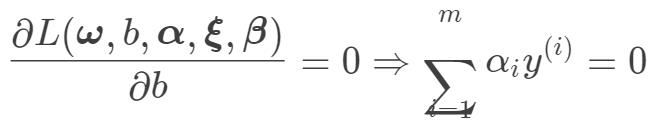
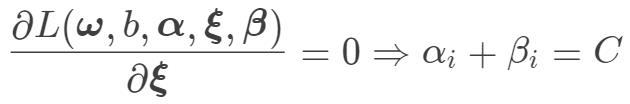
为存在约束 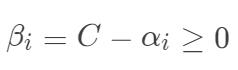，为了不失一般性, 我们可以
约束 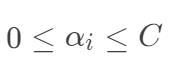， 从而去掉变量 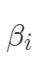。然后带入对应的对偶问题中，可以将对偶问题转为：

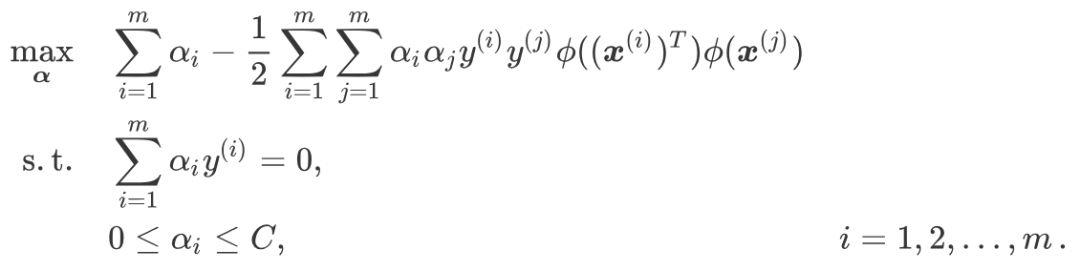
可以看到，软间隔支持向量机与硬间隔支持向量机的唯一区别在于对偶变量 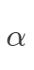的约束条件不同， 前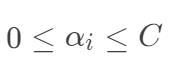者是 ，后者是 。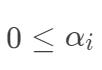

对于软间隔支持向量机，KKT条件如下：

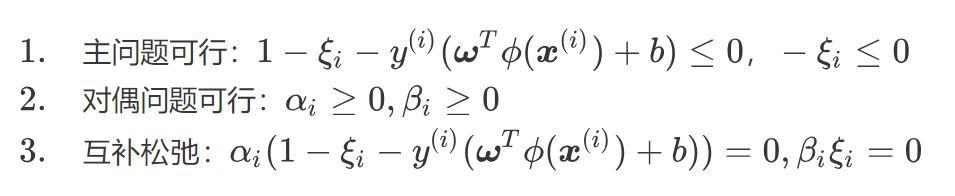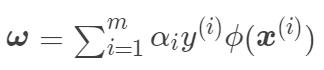将 带入到 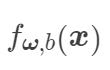中，这样，软间隔支持向量机的解的形式如下：

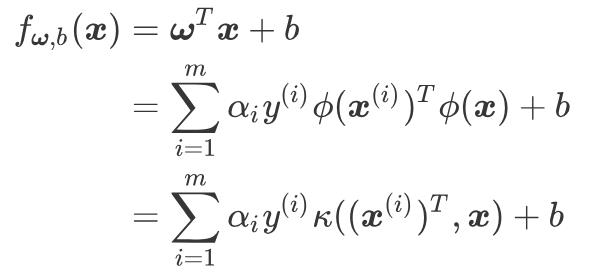
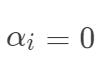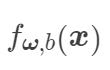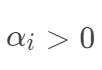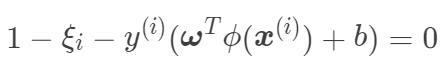根据上面的式子以及 KKT 中的互补松弛条件可知，如果 ，则该样本不会对有任何影响；如果 ，那么 ，即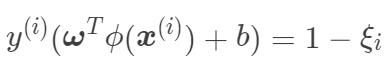，这时候可以进一步分为以下情况：

1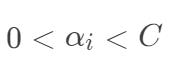），此时 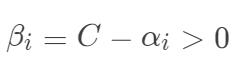，进而可以得到 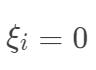，也就是该样本恰好落在最大间隔边界上。
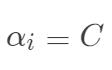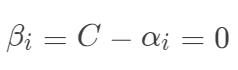2），此时 ，若 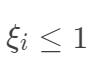，该样本落在最大间隔内部，若 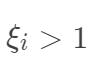,则该样本被错误分类。

综上可知，在软间隔支持向量机中, 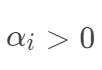对应的样本是支持向量，支持向量可以落在最大间隔边界、最大间隔边界内部或最大间隔边界外部（被错误分类的样本）。

参考：

1. 周志华.机器学习.第六章（支持向量机）

2. 深入浅出ML之Kernel-Based家族

   (http://www.52caml.com/head_first_ml/ml-chapter4-kernel-based-family/)

3. 从零推导支持向量机(SVM)

   (https://zhuanlan.zhihu.com/p/31652569)

4. 支持向量机通俗导论（理解SVM的三层境界）

   (https://blog.csdn.net/v_JULY_v/article/details/7624837)

（完）

---

---

最后说件事，我开通了知识星球，在星球里会分享我个人在数据分析/机器学习/深度学习/推荐系统方面的所学和所得。当前正在星球里分享我录制的机器学习视频课，如果想快速入门和提高自己，可以加入我的星球来交流（加入方式：扫描下方二维码或者点击“阅读原文”）。当前加入还可直接返现19.20元。

历史推荐

 | 

 

长按，识别二维码，加关注