入门支持向量机(SVM)原来这么简单
Posted AIrange
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了入门支持向量机(SVM)原来这么简单相关的知识,希望对你有一定的参考价值。
支持向量机(Support Vector Machine,SVM)
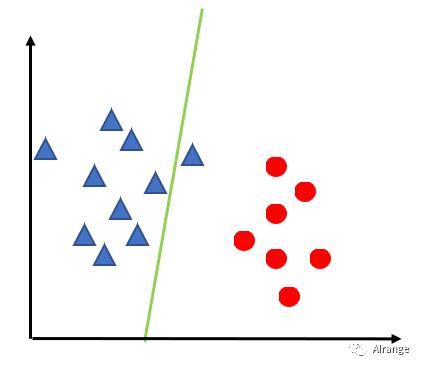
一个例子
接下来我们想找一个“分界线”把他们分开。
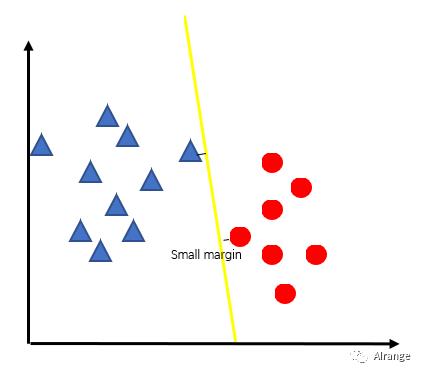
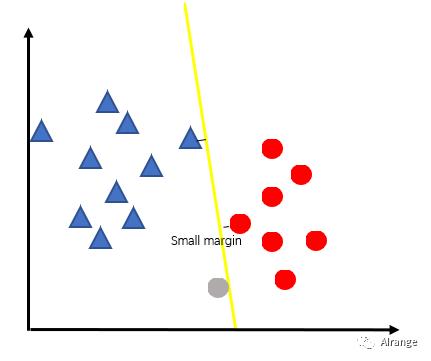
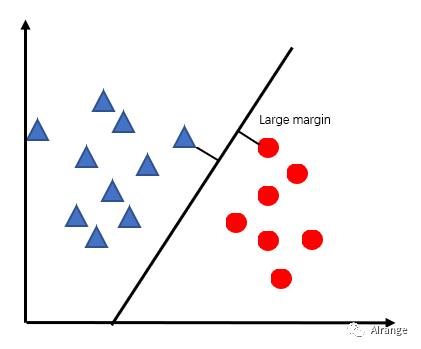
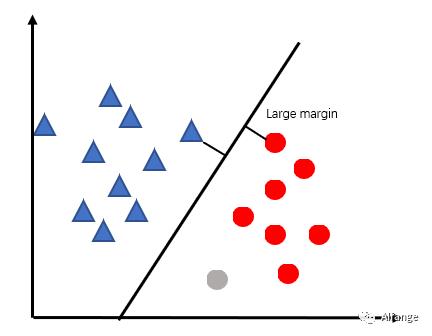
概念
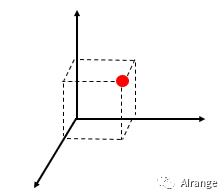
数据是如何分类的
什么是超平面
什么是支持向量(Support Vector)
应用
实例
1import numpy as np
2import matplotlib.pyplot as plt
3import pandas as pd
数据预处理
1#数据类型转换
2dataset[['age','estimatedsalary']]=dataset[['age','estimatedsalary']].astype(int)
3#设置特征和标签
4X = dataset.iloc[:, [0, 1]].values
5y = dataset.iloc[:, 3].values
6#划分训练集和测试集,300个为训练集,100个为测试集。
7from sklearn.model_selection import train_test_split
8X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
9#标准化
10from sklearn.preprocessing import StandardScaler
11sc = StandardScaler()
12X_train = sc.fit_transform(X_train)
13X_test = sc.fit_transform(X_test)
训练模型
1from sklearn.svm import SVC
2classifier = SVC(kernel='linear', random_state = 0)
3classifier.fit(X_train, y_train)
预测
1y_pred = classifier.predict(X_test)
1from sklearn.metrics import confusion_matrix
2cm = confusion_matrix(y_test, y_pred)
3cm

可以看到准确率为0.88。
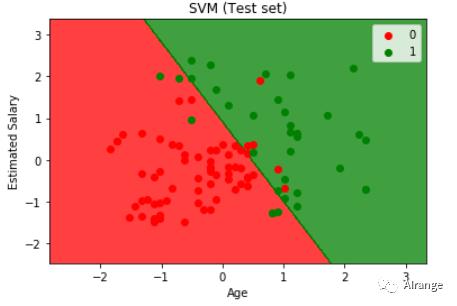
结果可视化如上图,测试集被这条线性边界分为两类。
超参数介绍

常涉及到的参数有下面三个:
正则化系数,C
(过拟合、泛化能力的名词解释见本文末尾)
kernel核函数
Gamma γ
调参——网格搜索
1from sklearn.model_selection import GridSearchCV,KFold, cross_val_score
2#设置超参数空间,设置每个超参数可能的取值。
3parameters={'kernel':('rbf','linear'),'C':[0.1,1,5,10],'gamma':[1,0.1, 0.01, 0.001]}
4kfold = KFold(n_splits=10,random_state=0) # 10折交叉验证,一种验证模型的方法
5classifier = SVC()
6#定义网格搜索对象,括号里的参数为分类器、超参数空间、验证模型的方法。
7clf = GridSearchCV(classifier,parameters,cv=kfold)
8clf.fit(X_train, y_train)
9print('最优模型对象',clf.best_estimator_)
10print('最优模型分数',clf.best_score_)
11print('最优模型参数',clf.best_params_)

预测结果并生成混淆矩阵
1from sklearn.metrics import confusion_matrix
2y_pred = clf.predict(X_test)
3
4cm = confusion_matrix(y_test, y_pred)
5cm
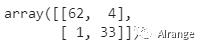
模型在测试集上的准确率提升至95%。
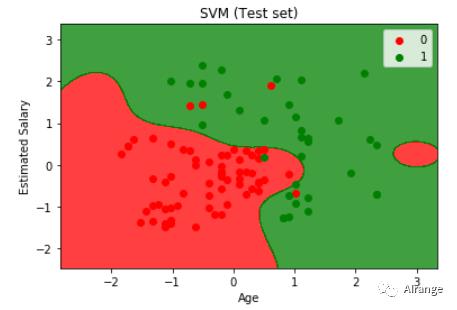
在此数据集上分数较高的模型采用rbf核函数,测试集的分类如上图所示。
知识补充
线性不可分情况
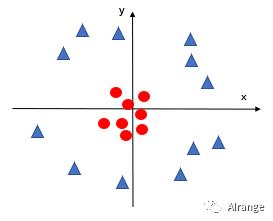
此时不能用简单的线性边界来区分两类。
接下来我们增加一维特征z,并且使
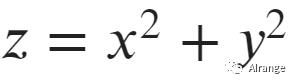
再投影到三维空间上去。
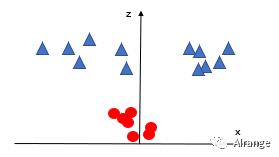
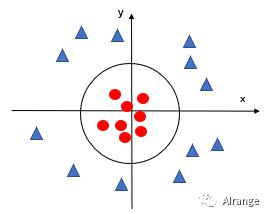
可以看到,现在可以将两类线性分割了。
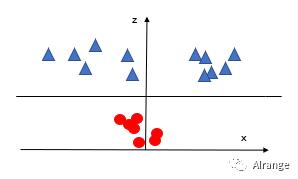
假设此时这条线性边界为z=4,那么也就是返回到二维空间上的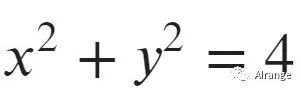 。
。
过拟合与欠拟合
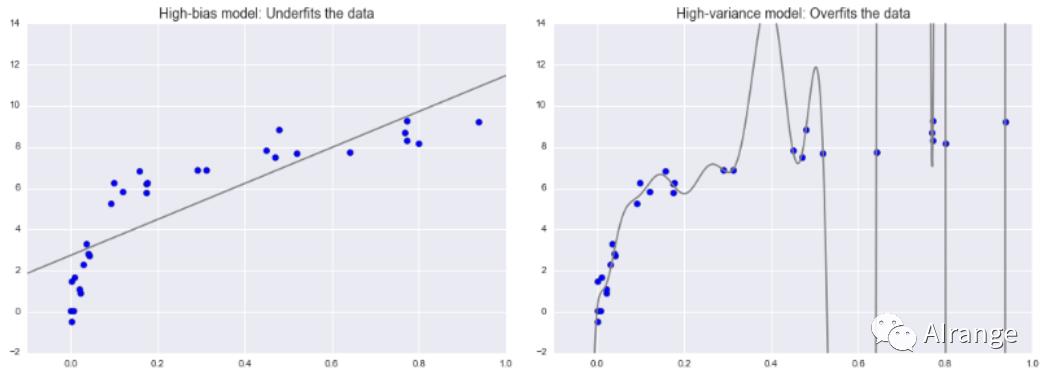
泛化能力
参考资料:
https://github.com/Avik-Jain/100-Days-Of-ML-Code
百度百科,支持向量机
机器学习—周志华
精彩内容回顾:
编辑:Sunam
以上是关于入门支持向量机(SVM)原来这么简单的主要内容,如果未能解决你的问题,请参考以下文章