换个角度看支持向量机

Posted 2021-04-26 月来客栈

在中，笔者介绍了什么是支持向量机以及如何来建模对应的优化问题，且同时那也是一种主流的理解支持向量机的视角。下面，笔者再来从另外一个角度来介绍什么是支持向量机。这两种理解支持向量机的方法有着截然不同的切入点，因此可以一起阅读以便对支持向量机有着更好的理解。

1 什么是支持向量机

SVM的全称是Support Vector Machine，即支持向量机。SVM主要也是用于解决分类问题的一个算法模型，属于有监督学习算法的一种。同时，SVM要解决的问题可以用一个经典的二分类问题加以描述。如下图(a)所示，两种不同颜色的二维数据点显然是可以被一条直线所分开，但是能将两类数据点分开的直线显然有无数条。图(b)和(c)中分别给出了两种不同的分类方案b和c（其中实线为分界线，术语称为“决策面”）。虽然在目前的数据上看，这两个分类器的分类结果是一样的，但如果考虑潜在的其他数据，则两者的分类性能明显是有差别的。

SVM算法认为分类器c在性能上要优于分类器b，其依据是c的分类间隔比b要大。所谓分类间隔是指：在保证决策面方向不变且不会出现错分样本的情况下移动决策面，然后在原来决策面的两侧会找到两个极限位置（越过该位置就会产生错分现象），而决策面到极限位置之间的距离就是分类间隔，即决策面到两条虚线之间的垂直距离就是这个策面对应的分类间隔。但显然每一个可能把数据集正确分开的决策面所对应的分类间隔通常都是不同的，而那个具有“最大间隔”的决策面就是SVM要寻找的最优解。那什么又叫“最大间隔”呢？

从上图可以发现，如果决策面并没有位于两条虚线之间的中间位置，那么所谓的分类间隔就有上下两个且不相等。但由于SVM在寻找最优决策面的过程中会同时最大化上下两个间隔，因此了满足两个间隔同时最大，那么最终得到的决策面就会位于两条虚线的中间（当没有明确的先验知识告诉我们决策面应该偏向于哪边时，最好的做法应该是居于中间的位置）。且此时两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为支持向量（support vector）。对于上图中的样本，分类器c所对应的决策面就是SVM寻找的最优决策面，而相应两个位于虚线上的样本点就叫做支持向量。同时，最优决策面的方向和位置也完全只取决于选择哪些样本点作为支持向量。

到这里，我们明确了SVM算法要解决的是一个最优分类器的设计问题。既然叫作最优分类器，其本质必然是个最优化问题。所以，接下来我们要讨论的就是如何把SVM变成用数学语言描述的最优化问题模型，这就是我们在接下来要讲的“SVM的数学建模”。

2 SVM的数学建模

一个最优化问题通常有两个最基本的因素：

①目标函数，也就是你希望什么东西的什么指标达到最好；

②优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。

在线性SVM算法中，目标函数显然就是那个“分类间隔”，而优化对象则是决策面。所以要对SVM问题进行数学建模，首先要对上述两个对象（“分类间隔”和“决策面”）进行数学描述。按照一般的思维习惯，我们先描述决策面。

2.1 决策面

我们暂时不纠结于 维空间中的 维超平面这种超出正常人想象力的情景，我们先来看看二维空间中的一条直线：

如方程 所示为二维平面中一条简单直线方程，现在我们做一个小小的改变让原来的 轴变成 轴， 变成 轴,于是 中的直线方程会变成下面的样子

方程 的向量形式可以写成：

进一步可以写成如下形式：

其中 （如果特殊说明，向量一般都指的是列向量）

2.2 分类间隔

我们在引例中介绍过分类间隔的定义及其直观的几何意义，并且说到SVM的核心思想就是最大化决策面与支持向量之间的间隔。但既然是最大化间隔，那首先得有的就是如何度量这个间隔。

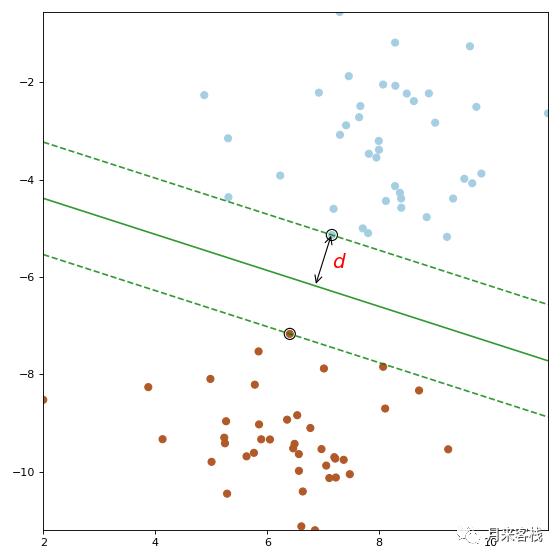
从图示可以看出，所谓的分类间隔其实就是点到直线的距离公式：

其中 是向量 的模，表示在空间中向量的长度； 为支持向量样本点的坐标。

由此可以，最大化分类间隔其实就是最大化 的一个过程。介绍到这里看起来我们已经找到了目标函数的数学形式，但问题当然也不会这么简单，我们还需要面对几个令人头痛的问题。

2.3 约束条件

上面说到问题，那到目前为止我们还面临着哪些问题呢？

①如何保证一条直线能够将所有的样本点都正确分类？

②即便找到了正确的决策面方向，还要保证决策面的位置应该在间隔区域的中轴线上，所以用来确定决策面位置的截距 也应该受到决策面方向和样本点分布的约束。

③即便取到了合适的方向和截距，公式 里面的 不应该是随随便便的一个样本点，而是支持向量对应的样本点。对于一个给定的决策面，我们该如何找到对应的支持向量？

以上三个麻烦的本质都是“约束条件”，也就是说我们要优化的变量的取值范围受到了限制和约束。尽管上面看起来是三条约束，但SVM算法通过一些巧妙的小技巧，将这三条约束条件融合在了一个不等式里面。

我们首先考虑一个决策面是否能够将所有的样本都正确分类的约束。对于上图中的蓝色和棕色样本点，我们为每个样本点 加上一个类别标签 ：

如果我们的决策面方程能够完全正确地对图示中的样本点进行分类，就会满足下面的公式:

那如果我们要求再高一点，要求决策面正好处于间隔区域的中轴线上，并且相应的支持向量对应的样本点到决策面的距离为 ，那么公式 就可以进一步写成：

接着我们对公式 中的两个不等式的左右两边除上 ，就可得到：

其中：

如果把 和 当成一条直线的方向向量和截距，你就会发现式子 和 事实上没有任何不同。因为直线 和直线 其实就是同一条直线，就像 同 一样。那现在让我忘记原来的直线方程参数 和 ，我们可以把参数  和 重新起个名字，仍旧叫它们 和 。因此我们可以直接说：“对于存在分类间隔的两类样本点，我们一定可以找到一些决策面，使其对于所有的样本点均满足下面的条件：

因此式子 可以认为是对SVM优化问题中约束条件的基本描述。

2.4 最大化分类间隔

想象一下公式 里面 的情况什么时候会发生呢？从式子 可以知道，只有当 是决策面 所对应的支持向量样本点时， 的情况才会成立，而这一点给了我们另一个简化目标函数的启发。回头看看公式 ，你会发现等式右边分子部分的绝对值符号内部的表达式正好跟式子 中不等式左边的表达式完全一致，无论原来这些表达式是 或者 ，其绝对值都是 。所以对于这些支持向量样本点有：

公式 的几何意义就是，支持向量样本点到决策面方程的距离就是 。我们原来的任务是找到一组参数 以使得分类间隔 最大化。此时根据公式对 的最大化问题就可以转变为对 的最小化问题，也等价于 的最小化问题。我们之所以要在 上加上平方和 的系数，是为了以后进行最优化的过程中对目标函数求导时比较方便，但这绝不影响最优化问题最后的解。

另外我们还可以尝试将公式 给出的约束条件进一步在形式上精练，把类别标签 和两个不等式左边相乘，形成统一的表述：

好了，到这里我们可以给出线性SVM最优化问题的数学描述了：

其中 表示样本点的总个数。

式子 描述的是一个典型的不等式约束条件下的二次型函数优化问题，同时也是支持向量机的基本数学模型。另外一点小建议就是，读到这里你可以试着在纸上随便画一些点，然后尝试用SVM的思想手动画线将两类不同的点分开。你会发现大多数情况下，你会先画一条可以成功分开两类样本点的直线，然后你会在你的脑海中想象去旋转这条线，旋转到某个角度你就会下意识的停下来，因为如果再旋转下去，就找不到能够成功将两类点分开的直线了；且与此同时你还可能来回的旋转这条直线以找到最优决策面，而这个过程就是对直线方向的优化过程。

3 总结

在本篇文章中，笔者从另外一个角度来介绍了什么是支持向量机以及SVM的数学建模问题。不同于上一篇文章中通过几何间隔与函数间隔来定义SVM的优化问题，本篇文章巧妙的运用了分类间隔+约束条件的方式，以一种更加自然的方式来描述SVM建模的整个过程。本次内容就到此结束，感谢阅读！

若有任何疑问与见解，请发邮件至[e-mail]并附上文章链接，青山不改，绿水长流，月来客栈见！

引用

[1]零基础学SVM https://zhuanlan.zhihu.com/p/24638007

[2]示例代码 ：https://github.com/moon-hotel/MachineLearningWithMe

近期文章