N10 神经网络支持向量机及K均值聚类

Posted 2021-04-26 数据实践笔记RENA

N10

  神经网络、支持向量机及K均值聚类

神经网络可以用于分类问题，也可以用于预测问题，特别是非线性关系预测问题。

• from sklearn.neural_network import MLPClassifier#神经网络分类模块

• from sklearn.neural_network import MLPRegressor#神经网络回归模块

支持向量机在小样本、非线性及高维模式识别中具有突出的优势。

• from sklearn import svm#支持向量机模块svm

聚类分析旨在找出数据对象之间的关系，对原数据进行分组打标签，标准是每个大组之间存在一定的

差异性，而组内的对象存在一定的相似性。

• from sklearn.cluster import KMeans#K-均值聚类模块KMeans

神经网络

1.模拟思想以及模型理解

大脑由非常多的神经元组成，各个神经元之间相互连接，形成一个非常复杂的神经网络。人工模拟大脑的学习训练模型，称为人工神经网络模型。

x1，x2，…，xn可以理解为n个输入信号（信息），w1，w2，…，wn可以理解为对n个信号的加权，从而得到一个综合信号（对输入信号进行加权求和）。神经元需要对这个综合信号做出反应，即引入一个阈值θ并与综合信号比较，根据比较的不同做出不同的反应，即输出y。这里用一个被称为激发函数的函数f（Σ-θ）来模拟其反应，从而获得反应值，并进行判别。

你蒙上眼睛，要判断面前的人是男孩，还是女孩。我们可以做一个简单的假设（大脑只有一个神经元），只用一个输入信号x1=头发长度（如50厘米），权重为1，则其综合信号Σ=x1=50，我们用一个二值函数作为激发函数：

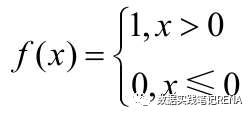
假设阈值θ=12，由于Σ=x1=50，故f（Σ-12）=f（38）=1，由此我们可以得到输出1为女孩，0为男孩。那么如何确定阈值是12，输出1表示女孩，而0表示男孩呢？这就要通过日常生活中的大量实践认识。

（1）取θ=1，这时判别正确率应该非常低。

（2）θ取值依次增加，假设θ=12时为最大，达到95%，当θ>12时，判别的正确率开始下降，故可以认为θ=12时达到判别正确率最大。这个时候，95%的男孩对应的函数值为0，同样95%的女孩对应的函数值为1。如果选用这个模型进行判别，其准确率达到95%。以上两步训练完成即得到参数θ=12，有95%的可能性输出1表示判别为女孩，输出0表示判别为男孩。

以上的分析只是便于理解，实际情况中比这复杂得多，人脑由上亿个神经元组成，其网络结构也非常复杂。

2.Python神经网络分类应用举例

仍以澳大利亚信贷批准数据集为例

import pandas as pddata = pd.read_excel('D:\study\程序与数据\第5章 Scikit-learn\credit.xlsx')x = data.iloc[:600,:14].valuesy = data.iloc[:600,14].valuesx1= data.iloc[600:,:14].valuesy1= data.iloc[600:,14].valuesfrom sklearn.neural_network import MLPClassifier#导入神经网络分类模块MLPClassifier。clf = MLPClassifier(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=(5,2), random_state=1)#利用MLPClassifier创建神经网络分类对象clf#MLPClassifier参数说明：#solver：神经网络优化求解算法，包括lbfgs、sgd、adam 3种，默认值为adam。#alpha：模型训练误差，默认值为0.0001。#hidden_layer_sizes：隐含层神经元个数，如果是单层神经元，设置具体数值即可，本例中隐含层有两层，即5×2。#random_state：默认设置为1即可。clf.fit(x, y);#调用clf对象中的fit（）方法进行网络训练rv=clf.score(x,y)#调用clf对象中的score（）方法，获得神经网络的预测准确率（针对训练数据）R=clf.predict(x1)#调用clf对象中的predict（）方法可以对测试样本进行预测，获得预测结果。Z=R-y1Rs=len(Z[Z==0])/len(Z)print('预测结果为：',R)print('预测准确率为：',Rs)

3.Python神经网络回归应用举例

以发电场数据为例，预测AT=28.4，V=50.6，AP=1011.9，RH=80.54时的PE

import pandas as pddata = pd.read_excel('D:\study\程序与数据\第5章 Scikit-learn\发电场数据.xlsx')x = data.iloc[:,0:4]y = data.iloc[:,4]from sklearn.neural_network import MLPRegressor#导入神经网络回归模块clf = MLPRegressor(solver='lbfgs', alpha=1e-5,hidden_layer_sizes=8, random_state=1)#利用MLPRegressor创建神经网络回归对象clfclf.fit(x, y);#调用clf对象中的fit（）方法进行网络训练rv=clf.score(x,y)#调用clf对象中的score（）方法，获得神经网络回归的拟合优度（判决系数）import numpy as npx1=np.array([28.4,50.6,1011.9,80.54])x1=x1.reshape(1,4)#预测样本的输入特征变量用x1表示R=clf.predict(x1)#调用clf对象中的predict（）可以对测试样本进行预测，获得预测结果。print('样本预测值为：',R)

支持向量机

1.基本内容

支持向量机在小样本、非线性及高维模式识别中具有突出的优势。支持向量机是机器学习中非常优秀的算法，主要用于分类问题，在文本分类、图像识别、数据挖掘领域中均具有广泛的应用。

支持向量机基于统计学习理论，强调结构风险最小化。基本思想是：对于一个给定有限数量训练样本的学习任务，通过在原空间或经投影后的高维空间中构造最优分离超平面，将给定的两类训练样本分开，构造分离超平面的依据是两类样本对分离超平面的最小距离最大化。

根据支持向量机原理，建立模型就是要 找到最优分离超平面（最大间隔分离样本的超平面）分开两类样本。最优分离超平面可以记为：

这样位于最优分离超平面上方的点满足：

位于最优分离超平面下方的点满足：

通过调整权重w，边缘的超平面可以记为：

H1：wTx+b≥1对所有的yi=+1

H2：wTx+b≤-1对所有的yi=-1

即落在H1或者其上方的为正类，落在H2或者其下方的为负类，得到：

落在H1或者H2上的训练样本，称为支持向量。

对于非线性可分的情形，可以通过非线性映射将原数据变换到更高维空间，在新的高维空间中实现线性可分。这种非线性映射可以通过核函数来实现。

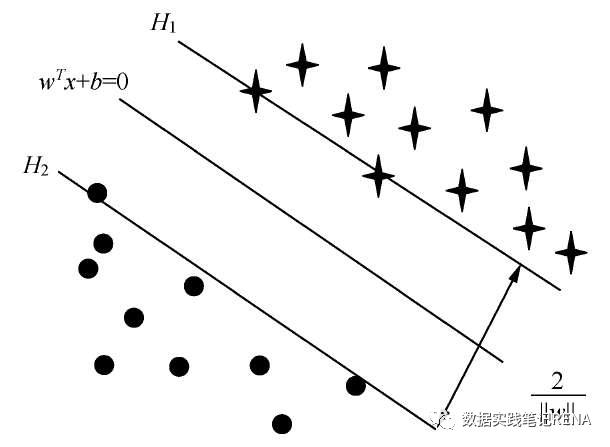
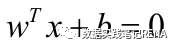
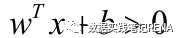
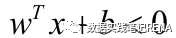
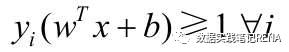
2.支持向量机应用举例

取自UCI公共测试数据库中的汽车评价数据集作为本例的数据集，该数据集共有6个特征、1个分类标签，共1728条记录，数据如表所示

a1-a6有不同的含义，以及d的取值情况1-4也有不同的含义

取数据集的前1690条记录作为训练集，余下的作为测试集，计算预测准确率。计算流程及思路如下：

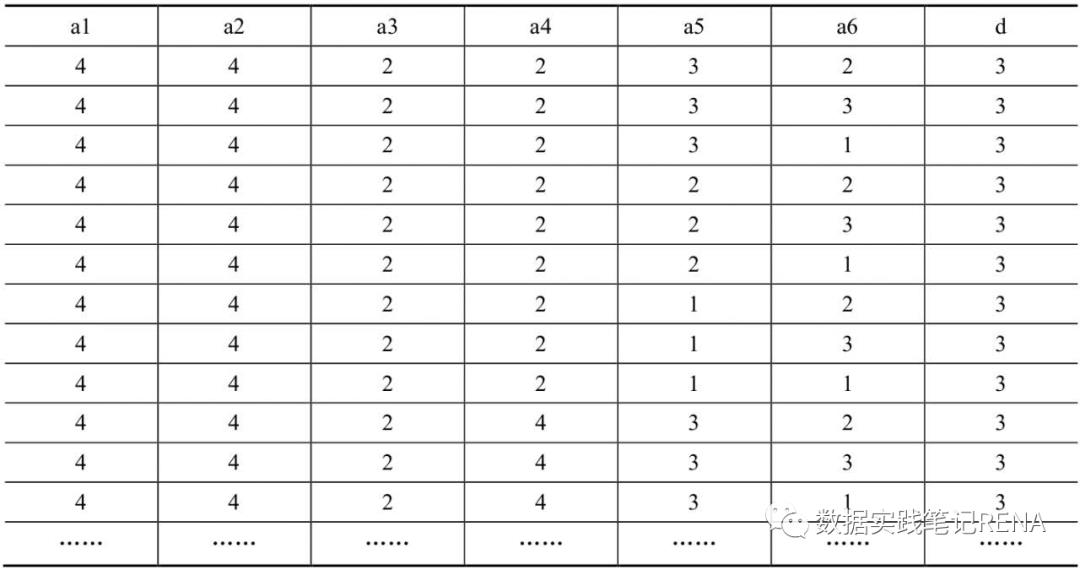
import pandas as pddata = pd.read_excel('D:\study\程序与数据\第5章 Scikit-learn\car.xlsx')#数据获取x = data.iloc[:1690,:6].valuesy = data.iloc[:1690,6].values#训练样本x1= data.iloc[1691:,:6].valuesy1= data.iloc[1691:,6].values#测试样本from sklearn import svm#导入支持向量机模块svmclf = svm.SVC(kernel='rbf')#利用svm创建支持向量机类svm。#其中核函数可以选择线性核、多项式核、高斯核、sig核，分别用linear、poly、rbf、sigmoid表示，默认情况下选择高斯核。clf.fit(x, y)#调用svm中的fit（）方法进行训练rv=clf.score(x, y);#调用svm中的score（）方法，考查训练效果R=clf.predict(x1)#调用svm中的predict（）方法，对测试样本进行预测，获得预测结果Z=R-y1Rs=len(Z[Z==0])/len(Z)print('预测结果为：',R)print('预测准确率为：',Rs)

K-均值聚类

1.聚类的思想

在样本之间定义距离，样本距离表明样本之间的相似度，距离越小，相似度越高，关系越紧密。将关系密切的聚集到一类，关系疏远的聚为另一类，直到所有样本都聚集完毕。

2.步骤

第1步:确定要分的 类别数目K。

第2步:确定K个类别的 初始聚类中心。这步要求在用于聚类的全部样本中，选择K个样本作为K个类别的初始聚类中心。

第3步:根据确定的K个初始聚类中心，依次计算每个样本到K个聚类中心的 欧氏距离，并根据距离最近的原则将所有的样本分到事先确定的K个类别中。

第4步:根据所分成的K个类别，计算出各类别中每个变量的均值，并以均值点作为 新的K个类别中心。重新计算每个样本到新中心的距离，并重新进行分类。

第5步:重复第4步，直到 满足终止聚类的条件为止。终止聚类的条件包括:(1)迭代次数达到研究者事先指定的最大迭代次数(SPSS 隐含的迭代次数是10次); (2)新确定的聚类中心点与上一次迭代形成的中心点的最大偏移量小于指定的量(SPSS隐含的是0. 02)。

可见，K-均值聚类法是根据事先确定的K个类别反复迭代直到把每个样本分到指定的类别中。类别数目的确定具有一一定的主观性， 需要依据研究者对研究问题的了解程度、相关知识和经验而定。

3.K-均值聚类算法举例

对给出的31个地区农村居民人均可支配收入情况做聚类分析

import pandas as pddata=pd.read_excel('D:\study\程序与数据\第5章 Scikit-learn\农村居民人均可支配收入来源2016.xlsx')X=data.iloc[:,1:]from sklearn.preprocessing import StandardScalerscaler = StandardScaler()scaler.fit(X)X=scaler.transform(X)#数据标准化处理from sklearn.cluster import KMeans#导入K-均值聚类模块KMeansmodel = KMeans(n_clusters = 4, random_state=0, max_iter = 500)#利用KMeans创建K-均值聚类对象model#参数说明:#n_clusters：设置的聚类个数K。#random_state：随机初始状态，设置为0即可。#max_iter：最大迭代次数。model.fit(X)#调用model对象中的fit（）方法进行拟合训练c=model.labels_#获取model对象中的labels_属性，可以返回其聚类的标签。Fs=pd.Series(c,index=data['地区'])Fm=Fs.sort_values(ascending=True)

扫二维码｜关注我的学习笔记

个人微信｜Gemini_Rena

入门Python 欢迎学术商讨与交流