支持向量机原理
Posted 小Q统计
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了支持向量机原理相关的知识,希望对你有一定的参考价值。
支持向量机(support vector machine,SVM)是经典的机器学习模型之一,最早由Cortes和Vapnik二人于1995年为解决二分类问题而提出。SVM有坚实的统计理论基础,且决策函数具有很强的几何含义。因其在模式识别等数据分析问题中的优越表现,SVM如今已发展成为一门经典的机器学习理论。本期我们来一起学习SVM的基本概念及在R中的使用方法。
1 线性支持向量机
1.1 硬间距支持向量机
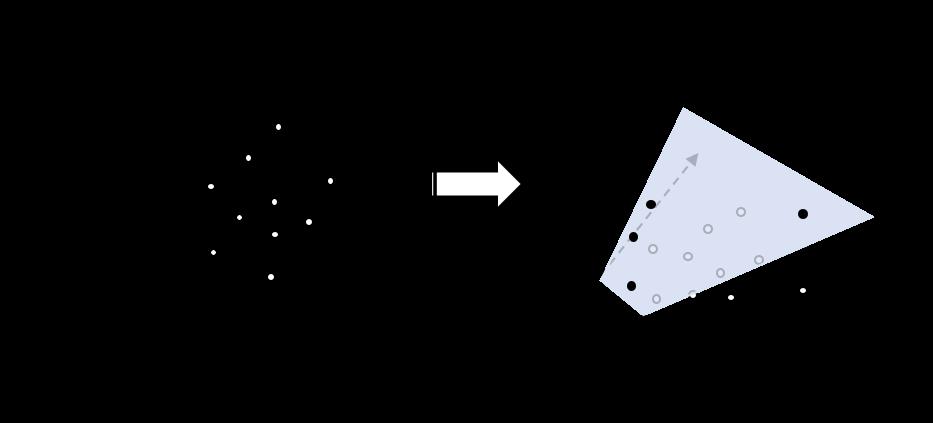
我们先来看一种简单的情形。假设我们得到的分类数据是线性可分的,也就是我们可以构造数据变量的一个不含交互项的线性函数作为分类的决策函数便可以实现分类的目的。例如下图(a)所示,对得到的二元变量数据(黑点+1和白点-1所示),我们直接用一条直线(三维空间是平面,三维以上是超平面)便可以实现分类的目的。这种情形便是前述的线性可分数据。
显然,对于上述的线性可分数据,我们只要把直线稍微倾斜一点便可以得到一个新的分类直线。那么,对于线性可分数据,如何寻找一条最优的分类超平面呢?

仔细观察图(a),对于不同的分类直线 ,我们是始终可以将其向两类数据进行平移直至恰好接触数据点(直线 和直线 ,如图(b)所示),显然分类直线 处在临界直线中间是合理的。我们自然希望得到的分类直线能够尽可能的将两类数据分开。换句话说,边界之间的 和直线 距离应当尽可能的大——当然,这是一种直觉上的判断,也是SVM理论的前提。
“如果你不认同这种直觉上的判断,那么…你可以静静的想一想看~
上述直观的认识便是硬间距(hard-margin)SVM的理论基础。现在我们用一些数学符号进行更为细致的描述。令 , 是第 个观测数据,其中 是一个 维的向量, 是分类标签。
假设我们的分类超平面为
其中 是超平面的法向量, 是超平面的截距项。按照前面直观的认识,我们的分类超平面需要最大化临界平面之间的距离,也即是
该模型没有体现分类超平面对数据分类,故而我们需要加上以下约束条件:
这里 为临界平面相对分类超平面移动值。注意到,如果令 和 ,那么上述的模型就可以等价的写成
现在,我们来看看临界距离如何表示。根据简单的几何知识,空间中任意一点 到给定平面的距离表示
经过 和 的变换之后,临界超平面上的点带入到超平面方程中等于1。那么临界平面之间的距离便为
因此,最终的模型可以等价得写成
“最小化 等价于最小化 .
以上便是硬间距SVM模型,也是最简单、最理想化的SVM分类模型。
1.2 软间距支持向量机
虽然硬间距SVM思想朴素,但是足以阐释SVM核心思想——最小化经验风险的同时最小化结构风险。尽管如此,硬间距SVM要求构建的分类超平面完全正确的分类所有训练数据,这显得非常严格。这样要求100%正确训练的模型容易产生过拟合,从而降低模型的泛化能力。
为了提升硬间距SVM的泛化能力以及扩大其应用场景,我们在训练SVM的过程中,允许数据被错误分类,这就得到了软间距(soft-margin)SVM,如图(c)所示。

从硬间距SVM的模型看出,不等式约束条件代表着分类超平面对数据的分类约束。我们允许数据被错误分类,也即是 大于一个小于1的数即可。换句话说,存在 ,满足
另一方面,违反约束的数据太多,我们得到的模型也不好。因此,我们在提升SVM的泛化能力同时,又希望违反约束的训练数据不能太多。
综上所述,软间距SVM模型就写成
其中 是调节参数,需事先给定,表示对违反约束的惩罚程度,数值越大表示模型期望的违反约束数据越少。一般来说, 要通过交叉验证来确定最优值。
软间距SVM描述的场景更加丰富,因此在实际运用中,我们也只采用该种形式的SVM模型。
2 模型的求解
SVM的求解算法一般通过优化其对偶模型得到最优解。为了方便描述,我们将软间距SVM模型写成矩阵形式
其中 是对角矩阵,对角元素为 ; 是一个长度为 、所有元素为1的向量; 是一个长度为 的向量。
首先,我们可以得到相应的Lagrangian方程
其中 是Lagrangian乘子向量。
接着,我们分别对 , 和 求偏导数并令为零得到
将上式结果带回到Lagrangian方程中,可以得到
结合约束条件可以得到SVM的对偶模型为
这是一个二次优化问题(quadratic programming problem,QPP),有很多成熟的算法可以求解。当然,很多学者针对SVM设计了一些计算快速的算法,如SMO、LIBSVM等。我们可以在R中利用程序包轻易的求解SVM模型,因此不再详述具体的算法。
求出 之后,我们根据Lagrangian的偏导数结果可得最终的决策函数为
可见,最终的决策函数只和 对应的训练数据 有关。
“那些 对应的训练数据 “支持”着最终的分类超平面的构建,因此被称为支持向量。这便是支持向量机名称的由来。
另一方面,优化SVM的过程需要满足KKT条件,其中之一为
可见,当 时,必有 ,此时不难看出数据点对应临近平面上的点或者错分类的点。由此看来,SVM模型的构建正是依赖于这些训练数据点。
“如果是硬间距SVM, 对应的便只是临界平面上的点——这更加可以看出”支持“二字的含义。
3 非线性支持向量机
软间距SVM有一个很大的缺陷,即依赖于数据是线性可分的假设。实际上,很多问题中的数据是非线性可分的,如图(d)所示。

这种情形应当如何处理呢?
Cortes和Vapnik采用了一种非常巧妙的方式。他们借助函数映射,将低维数据映射到高维空间中,使得原来不能线性可分的数据变得线性可分(这样的映射可以证明是始终存在的),如图(e)所示。
假设这种映射为
那么重复前面的优化过程不难得到需要优化的对偶模型为
一般来说,求解出具体的映射函数形式非常困难(或者根本就无法求出),我们如何解决该问题呢?Cortes和Vapnik注意到,SVM模型优化的过程中始终是保内积运算的。因此,他们利用空间映射和核函数的对应关系,将高维空间的内积运算 转换成核矩阵 的计算,从而实现非线性SVM的优化!
“核函数是一种特殊的函数,它与某个映射 的内积运算对应。映射函数难以给出,但可以根据核函数的特征来给定某种形式。由于我们不知道具体的映射,因此核函数的给定是一种尝试。
常见的核函数有:
-
线性核: ; -
高斯核: , ; -
Sigmoid核: , ;
核矩阵 是一个 的矩阵,其中第 元素为 。
最后,我们得到非线性SVM的分类超平面为
我们仍然可以看到,最终的超平面的构建只和 对应的训练样本点有关。
4 R求解支持向量机
目前在R中比较常用的SVM求解程序包是e1071包。我们首先安装并载入该程序包:
install.packages("e1071")
library(e1071)
我们用R中的鸢尾花数据集建立SVM模型,该数据中包含三种鸢尾花(分别标记为setosa、versicolor和virginica)的花萼和花瓣数据,最早由1936年Fisher发表的一篇重要论文给出。
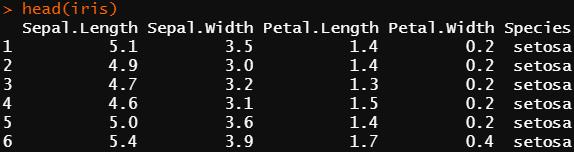
我们以花瓣的长度核宽度为变量做出数据的图像,可见setosa和另外两种花很好的区分开来。我们下面选择versicolor和virginica进行SVM建模。
e1071中求解SVM的函数为svm,它的基本用法如下
svm(formula, data= NULL, subset, na.action = na.omit , scale= TRUE)
# formula为拟合的公式
# data为数据集
参数na.action用于指定当样本数据中存在无效的空数据时系统应该进行的处理。默认值na.omit表明程序会忽略那些数据缺失的样本。另外一个可选的赋值是na.fail,它指示系统在遇到空数据时给出一条错误信息。参数scale为一个逻辑向量,指定特征数据是否需要标准化(默认标准化为均值0,方差1)。索引向量subset用于指定那些将被来训练模型的采样数据。
我们首先拟合一个基本的模型
partdata <- subset(iris, Species %in% c("versicolor","virginica"))
fit <- svm(Species~Petal.Length + Petal.Width, data = partdata)
查看结果为
> summary(fit)
Call:
svm(formula = Species ~ Petal.Length + Petal.Width, data = partdata)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
Number of Support Vectors: 23
( 12 11 )
Number of Classes: 2
Levels:
versicolor virginica
通过summary函数可以得到关于模型的相关信息。其中,SVM-Type项目说明本模型的类别为C-SVM(SVM发展至今已有很多类型的SVM,上述介绍的为最基本的C-SVM);SVM-Kernel项说明本模型所使用的核函数为高斯内积函数且核函数;cost项目说明本模型确定的约束违反成本为1。而且我们还可以看到,模型找到了23个支持向量:第一类包含有12个支持向量,第二类包含有11个支持向量。
当然,我们还可以利用程序包得到分类的示意图,可见模型还是训练的不错的。
更加详细的使用方式,有兴趣的读者可以自行阅读相关文档进行实践。
5 结语
本次我们主要学习了经典支持向量机的基本概念核求解算法,并用一个简单的案例介绍R求解SVM的方式。支持向量机发展至今已有很多种衍生类型,但它们的基本思想是共同的。感兴趣的读者可以进一步阅读相关文献材料。
喜欢小Q的文章,欢迎点赞分享。有问题的读者,敬请留言讨论。
以上是关于支持向量机原理的主要内容,如果未能解决你的问题,请参考以下文章