向量的点乘和叉乘的区别.详细点.高手进

Posted 2023-03-14

1、表示意义不同：

点乘是向量的内积。 

叉乘是向量的外积。

2、结果单位不同：

点乘，结果是一个向量在另一个向量方向上投影的长度，是一个标量。

叉乘，也叫向量积。结果是一个和已有两个向量都垂直的向量。

3、计算方法不同：

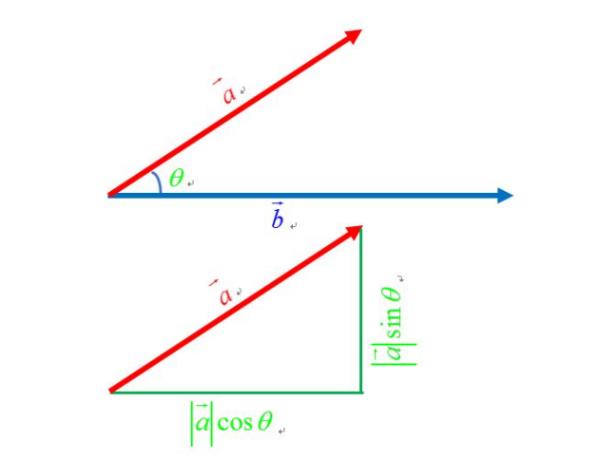
点乘，公式：a * b = |a| * |b| * cosθ

叉乘，公式：a ∧ b = |a| * |b| * sinθ

扩展资料

点乘又叫向量的内积、数量积，是一个向量和它在另一个向量上的投影的长度的乘积。

该定义只对二维和三维空间有效。

这个运算可以简单地理解为：

在点积运算中，第一个向量投影到第二个向量上（这里，向量的顺序是不重要的，点积运算是可交换的），然后通过除以它们的标量长度来“标准化”。

这样，这个分数一定是小于等于1的，可以简单地转化成一个角度值。

叉乘的几何意义及其运用

叉积的长度|a×b|可以解释成这两个叉乘向量a，b共起点时，所构成平行四边形的面积。

据此有：混合积[abc]=（a×b）·c可以得到以a，b，c为棱的平行六面体的体积。

参考资料

百度百科-点积

百度百科-向量积

参考技术A 用"*"表示点乘符号，(a,b)表示向量a与向量b的夹角

向量的点乘积是一个数
a*b=|a|×|b|×coc(a,b)

向量的叉乘积是一个向量，它的模是
|a×b|=|a|×|b|×sin(a,b)
它的方向按右手定则判定：弯曲右手手掌(称赞别人时所做的动作)，拇指向外，另外四指弯曲的方向与从a到b的转角方向相同，拇指所指的方向即是a×b的方向. 参考技术B 向量的点乘积是一个数
a*b=|a|×|b|×coc(a,b)

向量的叉乘积是一个向量，它的模是
|a×b|=|a|×|b|×sin(a,b)
它的方向按右手定则判定：弯曲右手手掌(称赞别人时所做的动作)，拇指向外，另外四指弯曲的方向与从a到b的转角方向相同，拇指所指的方向即是a×b的方向. 参考技术C 我觉得不应该仅限于二维、三维，应该可以推广到三维以上，而且含义不变。 参考技术D 向量的点积：

假设向量u(ux, uy)和v(vx, vy)，u和v之间的夹角为α，从三角形的边角关系等式出发，可作出如下简单推导：

|u - v||u - v| = |u||u| + |v||v| - 2|u||v|cosα

===>

（ux - vx）2 + (uy - vy)2 = ux2 + uy2 +vx2+vy2- 2|u||v|cosα

===>

-2uxvx - 2uyvy = -2|u||v|cosα

===>

cosα = (uxvx + uyvy) / (|u||v|)

这样，就可以根据向量u和v的坐标值计算出它们之间的夹角。

定义u和v的点积运算： u . v = (uxvx + uyvy)，

上面的cosα可简写成： cosα = u . v / (|u||v|)

当u . v = 0时（即uxvx + uyvy = 0），向量u和v垂直；当u . v > 0时，u和v之间的夹角为锐角；当u . v < 0时，u和v之间的夹角为钝角。

可以将运算从2维推广到3维。

向量的叉积：

假设存在向量u(ux, uy, uz), v(vx, vy, vz), 求同时垂直于向量u, v的向量w(wx, wy, wz).

因为w与u垂直，同时w与v垂直，所以w . u = 0, w . v = 0; 即

uxwx + uywy + uzwz = 0;
vxwx + vywy + vzwz = 0;

分别削去方程组的wy和wx变量的系数，得到如下两个等价方程式：

(uxvy - uyvx)wx = (uyvz - uzvy)wz
(uxvy - uyvx)wy = (uzvx - uxvz)wz

于是向量w的一般解形式为：

w = (wx, wy, wz) = ((uyvz - uzvy)wz / (uxvy - uyvx), (uzvx - uxvz)wz / (uxvy - uyvx), wz)
= (wz / (uxvy - uyvx) * (uyvz - uzvy, uzvx - uxvz, uxvy - uyvx))

因为：

ux(uyvz - uzvy) + uy(uzvx - uxvz) + uz(uxvy - uyvx)
= uxuyvz - uxuzvy + uyuzvx - uyuxvz + uzuxvy - uzuyvx
= (uxuyvz - uyuxvz) + (uyuzvx - uzuyvx) + (uzuxvy - uxuzvy)
= 0 + 0 + 0 = 0

vx(uyvz - uzvy) + vy(uzvx - uxvz) + vz(uxvy - uyvx)
= vxuyvz - vxuzvy + vyuzvx - vyuxvz + vzuxvy - vzuyvx
= (vxuyvz - vzuyvx) + (vyuzvx - vxuzvy) + (vzuxvy - vyuxvz)
= 0 + 0 + 0 = 0

由此可知，向量(uyvz - uzvy, uzvx - uxvz, uxvy - uyvx)是同时垂直于向量u和v的。

为此，定义向量u = (ux, uy, uz)和向量 v = (vx, vy, vz)的叉积运算为：u x v = (uyvz - uzvy, uzvx - uxvz, uxvy - uyvx)

上面计算的结果可简单概括为：向量u x v垂直于向量u和v。

根据叉积的定义，沿x坐标轴的向量i = (1, 0, 0)和沿y坐标轴的向量j = (0, 1, 0)的叉积为：

i x j = (1, 0, 0) x (0, 1, 0) = (0 * 0 - 0 * 1, 0 * 0 - 1 * 0, 1 * 1 - 0 * 0) = (0, 0, 1) = k

同理可计算j x k:

j x k = (0, 1, 0) x (0, 0, 1) = (1 * 1 - 0 * 0, 0 * 0 - 0 * 1, 0 * 0 - 0 * 0) = (1, 0, 0) = i

以及k x i:

k x i = (0, 0, 1) x (1, 0, 0) = (0 * 0 - 1 * 0, 1 * 1 - 0 * 0, 0 * 0 - 0 * 0) = (0, 1, 0) = j

由叉积的定义，可知：

v x u = (vyuz - vzuy, vzux - vxuz, vxuy - vyux) = - (u x v)

我的OpenGL学习进阶之旅向量点乘和叉乘的几何意义

一、点乘和叉乘

两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的，因为它在视觉上是没有意义的。但是在相乘的时候我们有两种特定情况可以选择：一个是点乘(Dot Product)，记作
$$v$$