图解希尔排序Shellsort

Posted 2021-04-25 AlgorithmsML

希尔排序（ShellSort）是以它的发明者Donald Shell名字命名的，希尔排序是插入排序的改进版，实现简单，对于中等规模数据的性能表现还不错。

Shellsort思想

为何改进插入排序？因为插入排序仅对小规模数据或者基本有序的数组十分高效。但基本有序或规模较小都不常见，而希尔排序可以将较大规模并且无序的数据分割成多个小规模数据，再由插入排序对小规模的数组排序（高效），而且这些小规模的数据之间间隔为h，能将元素交换到很远的地方，再一步高效。

   

图解Shellsort

首先它把较大的数据集合分割成若干个小组（逻辑上分组！！！），然后对每一个小组分别进行插 入排序，此时，插入排序所作用的数据量比较小（每一个小组），插入的效率比较高

下面有颜色的是逻辑上的分组，并没有实际地进行分组操作，在数组中的位置还是原来 的样子，只是将他们看成这么几个分组（逻辑上分组）。可以看出，他是按下标相隔距离为4分的组，也就是说把下标相差4的分到一组，比如这 个例子中a[0]与a[4]是一组、a[1]与a[5]是一组...，这里的差值（距离）被称为增量h。

对每个分组进行插入排序：

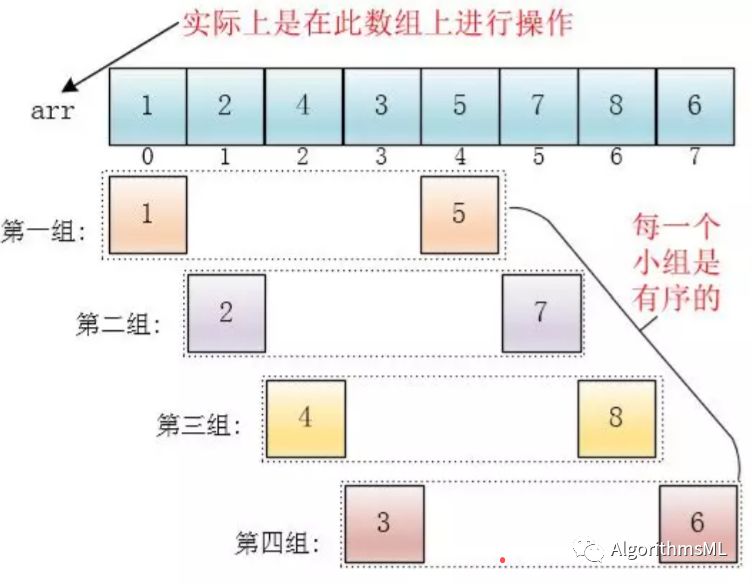
此时，整个数组变的部分有序了（有序程度可能不是很高，但是部分有序对于插入排序已然高效）

缩小增量为原来一半h=2，继续划分分组：

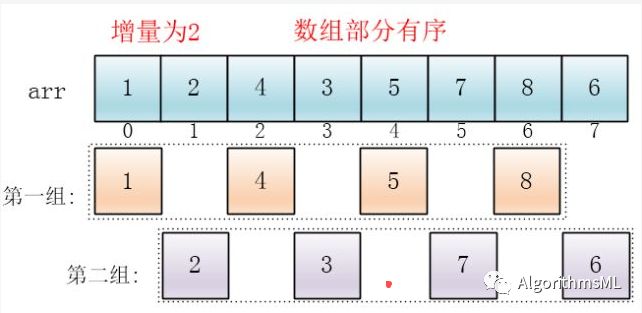
同理对每个分组进行排序（因为部分有序，插入排序高效），使其每个分组各自有序：

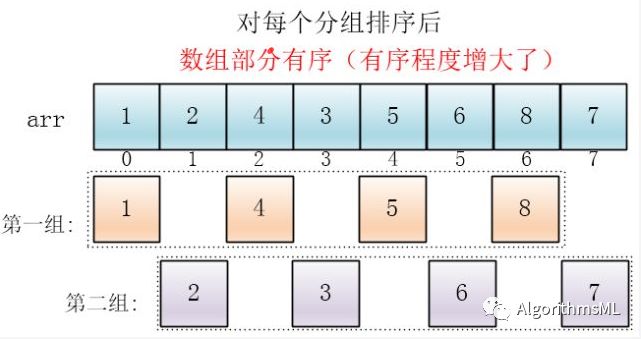
再缩小增量为原来一半h=1（终止），继续划分分组：

再进行排序，则所有排序完成。

时间复杂度

值得注意的是，shellsort算法简单，但时间复杂度分析极其复杂。希尔排序的复杂度和增量序列是相关的，有的增量序列的复杂度至今还没人能够证明出来。

{1,2,4,8,...}这种序列并不是很好的增量序列，使用这个增量序列的时间复杂度（最坏情形）是O(n^2)

Hibbard提出了另一个增量序列{1,3,7，...,2^k-1}，这种序列的时间复杂度(最坏情形)为O(n^1.5)

Sedgewick提出了几种增量序列，其最坏情形运行时间为O（n^1.3）,其中最好的一个序列是{1,5,19,41,109,...}