算法希尔排序

Posted 2021-04-25 暗星涌动

基本概念：

希尔排序是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破O(n2）的第一批算法之一。

希尔排序就是通过将元素数组划分为若干小组，然后对各个小组进行插入排序来减低元素之间对比的次数，提高排序的效率。

基本思想：

选择步长 div 将数组划分为若干小组（即所有距离为div 的倍数的记录放在同一个组中），对各个小组分别进行排序，排序完成之后，每一个组的元素都是有序的。然后不断将步长 div 缩小，不断分组和排序，直到最后 div = 1，算法变为插入排序，这就保证了数据一定会被排序。

实例讲解：

已知数组 arr [ 10 ] = { 5，4，8 ， 0 ， 9 ，3 ， 2， 6 ，7 ， 1 } 。假定步长 div [ 3 ] = { 5 , 2 , 1 } 

第一轮排序（颜色相同为一组）：

将数组分成 5 个子序列 { 5 , 3 } ， { 4 , 2 } ，{ 8 , 6 } ，{0 , 7 } ，{ 9 , 1 } 。如下列所示：

5                                    3                      

      4                                    2

             8                                    6

                     0                                    7

                             9                                    1

对上面每个子序列分别进行排序后得到：

3 ，2 ，6 ，0 ，1 ，5 ，4 ，8 ，7 ，  9

第二轮排序（颜色相同为一组）：

将数组分成两个子序列 { 3 ，6 ， 1 ,  4，7 } ， { 2 ，0 ，5 ，8 ， 9} 。如下列所示：

3            6            1            4              7 

       2             0            5            8              9

对上面每个子序列分别进行排序后得到：

1 ， 0 ，3 ，2 ，4 ，5 ，6 ，8 ，7 ， 9

第三轮排序：

对整个数组排序，得到最后的结果：

0 ，1 ，2 ，3 ，4 ， 5， 6 ，7 ， 8 ，9 

数据结构（C语言版）：

#include<stdio.h>

int n;

void ShellInsert(int *a,int div)
{
    int i,j;
    for(i=div+1;i<=n;i++)
    {
    //为什么 i=div+1 ? 因为 a [0] 没有赋值，所以待排序序列的下标从 1 开始  
        if(a[i]<a[i-div])
        {
            a[0]=a[i];
            for(j=i-div;j>0&&a[0]<a[j];j-=div)
                a[j+div]=a[j];
            a[j+div]=a[0];
        }
    }
}

void ShellSort(int *a,int *div,int t)
{
    int i,j;
    for(i=0;i<t;i++)
    {
        ShellInsert(a,div[i]);
        printf("排序后得到：\n");
        for(j=1;j<=n;j++)
            printf("%d ",a[j]);
        printf("\n");
    }
}

int main()
{
    int i,t,a[100],div[100];
    scanf("%d",&n);
     
    div[0]=n/2;
    for(i=1;;i++)
    {
        div[i]=div[i-1]/2;
         if(div[i]==1)
              break;
    }
    t=i+1;
    for(i=1;i<=n;i++)
        scanf("%d",&a[i]);

    ShellSort(a,div,t);
    
    return 0;
}

演示结果：

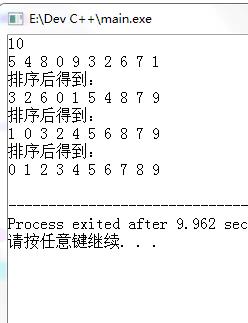
一开始我并不了解为什么 i = div + 1 ，于是我找到了下面这种写法（个人觉得下面这种比较容易理解）：

#include<stdio.h>

int n;

void Swap(int *a,int *b)
{
    int c=*a;
    *a=*b;
    *b=c;
}

void Shell(int *a,int n)
{
    if(n<=1)
        return ;
    int div,i,j,k;
    for(div=n/2;div>=1;div/=2)
    {
        for(i=0;i<=div;i++)
        {
            for(j=i;j<n-div;j+=div)
            {
                for(k=j;k<n;k+=div)
                    if(a[j]>a[k])
                        Swap(a+j,a+k);
            }
        }

        for(i=0;i<n;i++)
            printf("%d ",a[i]);
        printf("\n");
    }
}

int main()
{
    int i,j,a[100];
    scanf("%d",&n);
    for(i=0;i<n;i++)
        scanf("%d",&a[i]);

    Shell(a,n);
    return 0;
}

演示结果：

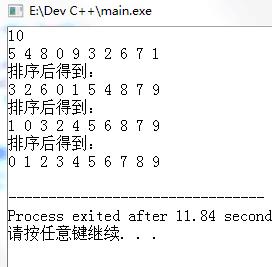
希尔排序时间复杂度
希尔排序的时间复杂度与增量(即，步长div)的选取有关。例如，当增量为1时，希尔排序退化成了直接插入排序，此时的时间复杂度为O(N²)，而Hibbard增量的希尔排序的时间复杂度为O(N3/2)。

希尔排序稳定性
希尔排序是不稳定的算法。对于相同的两个数，可能由于分在不同的组中而导致它们的顺序发生变化。
算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

由于个人能力有限，上述代码若有不足之处，敬请指出，谢谢。