浅谈复杂排序之希尔排序！
Posted 遇见未来世界
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了浅谈复杂排序之希尔排序！相关的知识，希望对你有一定的参考价值。
希尔排序是插入排序的一种，又称缩小增量排序，是直接插入排序的一种更为高效的改进版，由于算法是由Donald Shell提出的，故名希尔排序
复杂排序包含很多种，常见的大概有以上几种，这里就希尔排序作简要介绍。
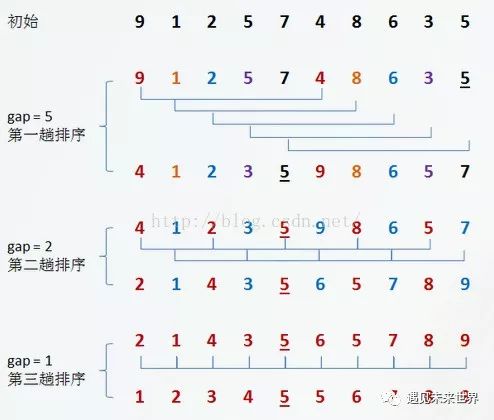这里的希尔排序与直接插入排序最大的不同在于增加了比较的效率，同时也在一定程度上减少了元素的移动，需要注意的是这里每一趟排序i一直在按顺序依次往后移，第一次从i=gap开始，直到i增加到元素数组最后，到了第二趟会发现会出现两层，其实就是一层，因为每次都是上边一层执行一格，下班执行一格，只是看起来是两层，理解起来好理解，到了第三趟仍然是相邻gap个比较，当gap=1时，即执行最后一趟循环。接下来再看一个例子。
由于数组中有十个元素，初始取gap=n/2=5，n只是在第一趟循环有用，这里的i也从5开始，一直到i=n-1。
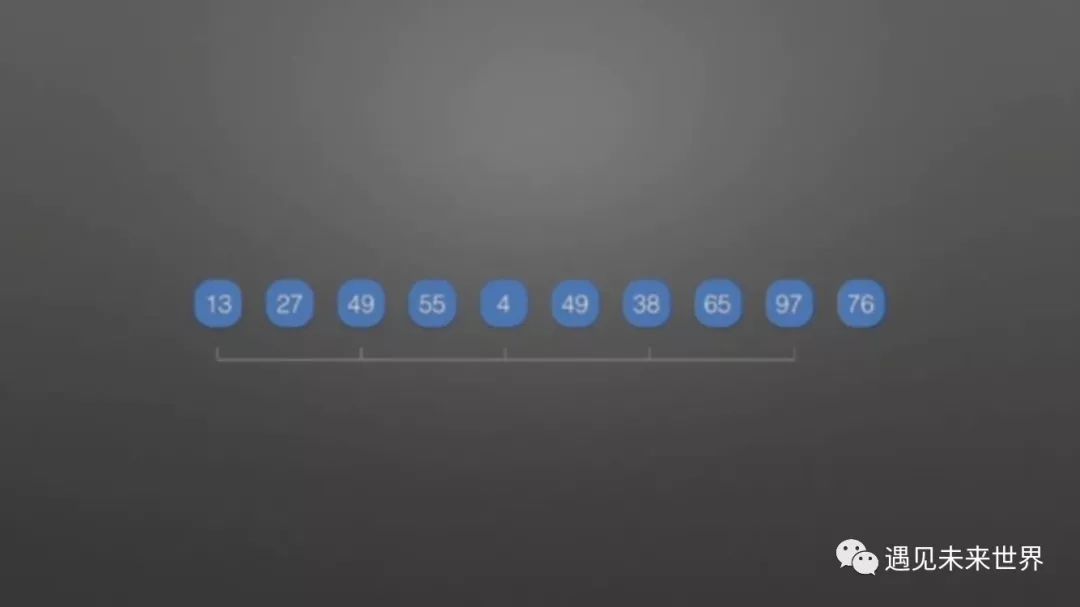第二趟gap往下取整，gap/2=2，i便从i=2开始循环比较。
这形式上的一层下来，这几个便按照从小到大完成了排序，实际上这并不是连续进行的。
最后第三趟，i=1，两两相邻比较，完成最后的调整。
此时，希尔排序已经完成了对该数组的排序操作，接下来看代码。
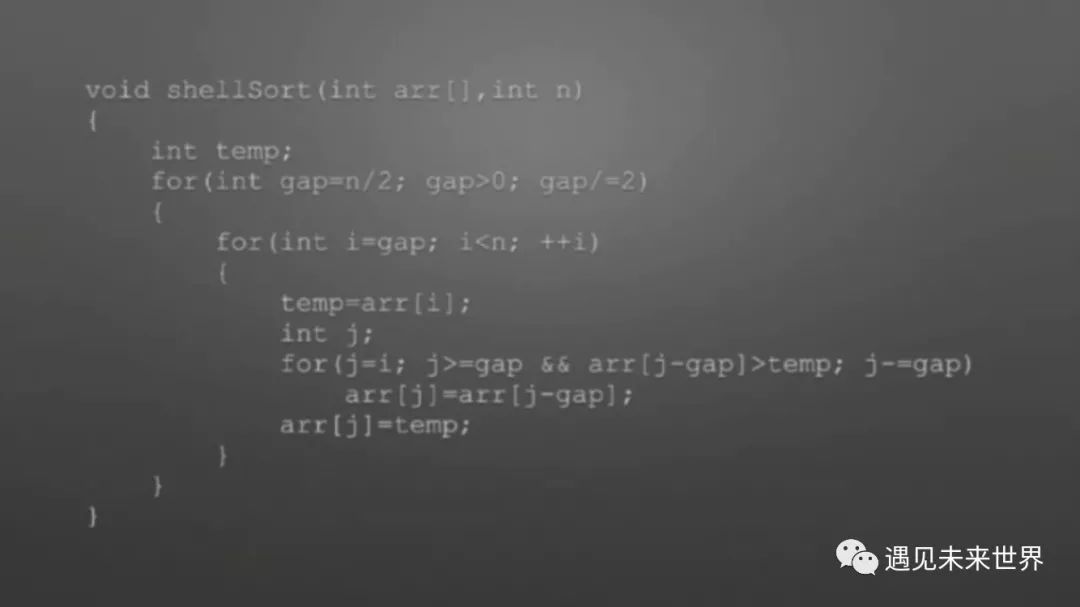这是希尔排序的算法实现，接着对代码进行图形化理解。
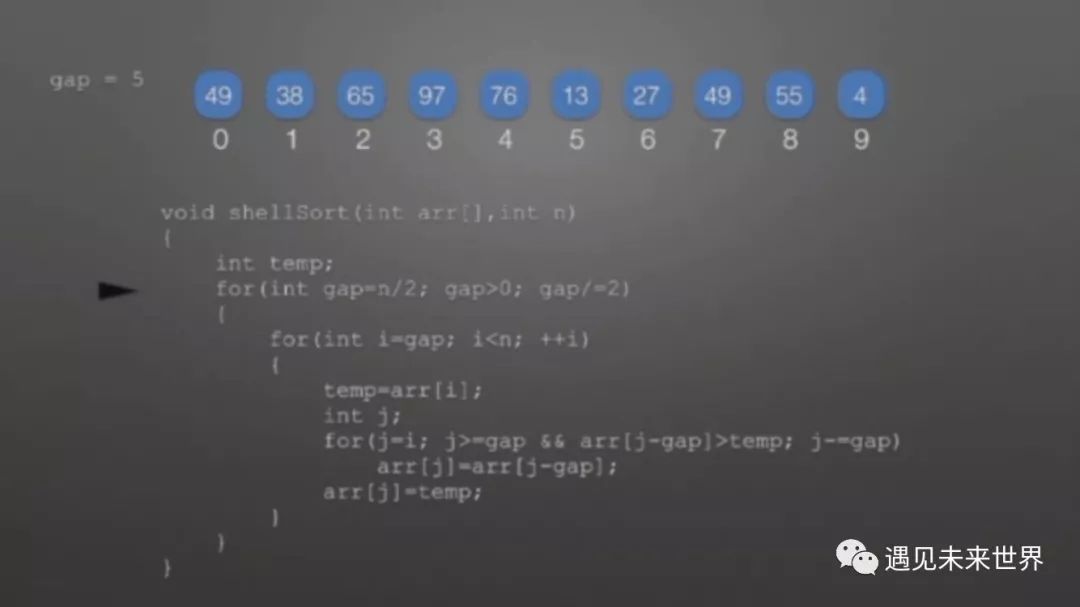循环刚开始，根据数组规模n确定gap初始值，之后gap二分减少，与n不再有关，这里第一次n=5。
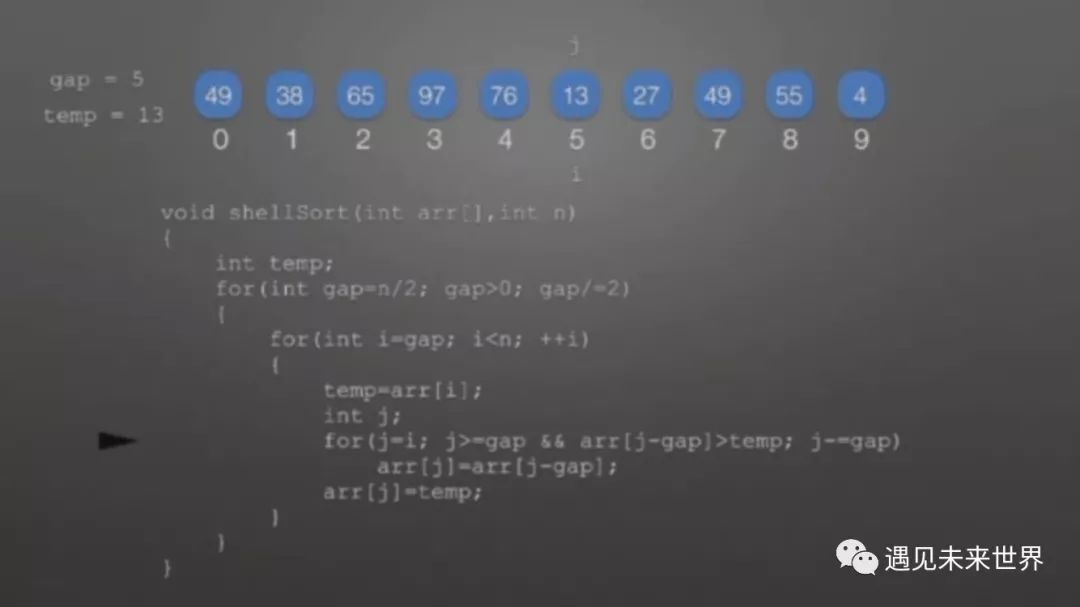接着，由n=5便确定i从数组中那个元素开始，即a【i】，之后i顺序增加，直到i=n-1，即数组中的最后一个元素，再往下按gap间隔进行比较。
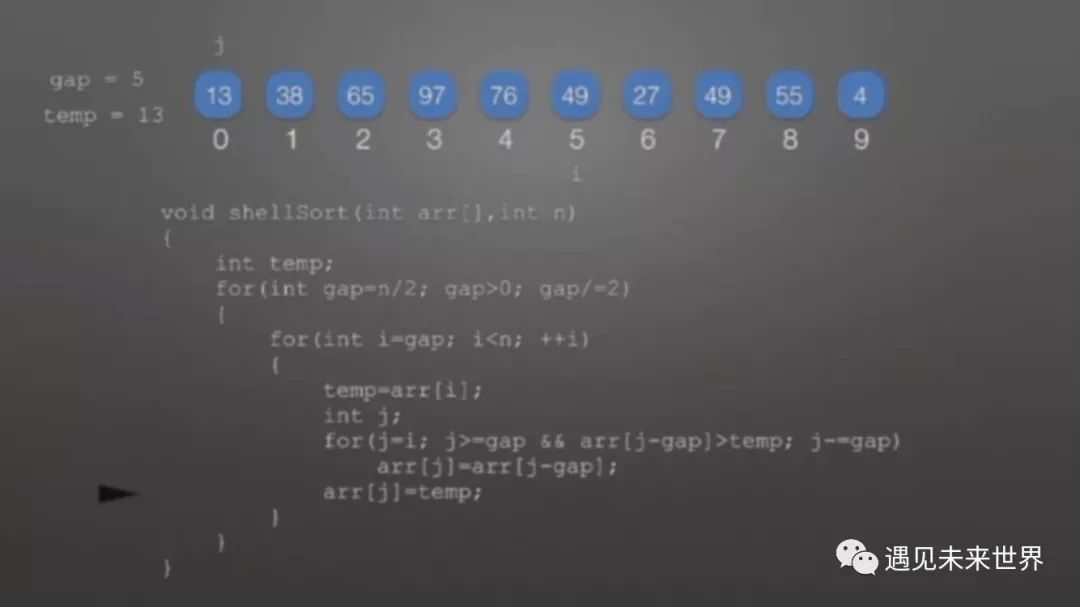要进行比较，首先得有两个元素才存在可比性，我们已知a【i】和gap，于是便可知另一个元素为a【j】，j=i-gap，由于可能需要交换，所以需要一个temp变量保存a【i】的值，保证元素不会丢失，这里发生交换的条件有两个，第一j需要不小于gap。j的初始值为i，是这个程序的精华之处，有人问j为什么不能是直接i-gap，因为这就降低程序的健壮性，j如果等于i-gap，就无法再灵活的变化，但其实j也不会变化因为后边都是在前边排好序进行的，就算是j执行到了第二次循环j=j-gap，也无法满足循环体的条件arr【j-gap】>temp，所以仍然是一层执行一个，当然每层的间隔都是gap。这里=j=j-gap为后边提供了很大的方便，可以直接使arr【j】=gap，因为j已经变成了i-gap。
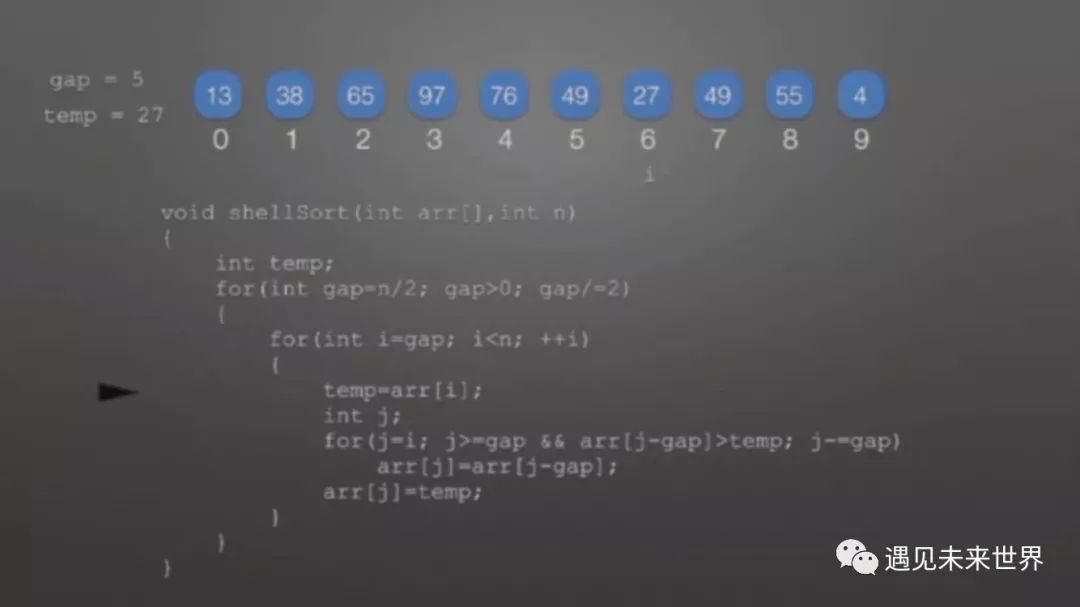完成这次循环后，i后移，接着进行下一层的比较，依次循环，直到i=n-1。
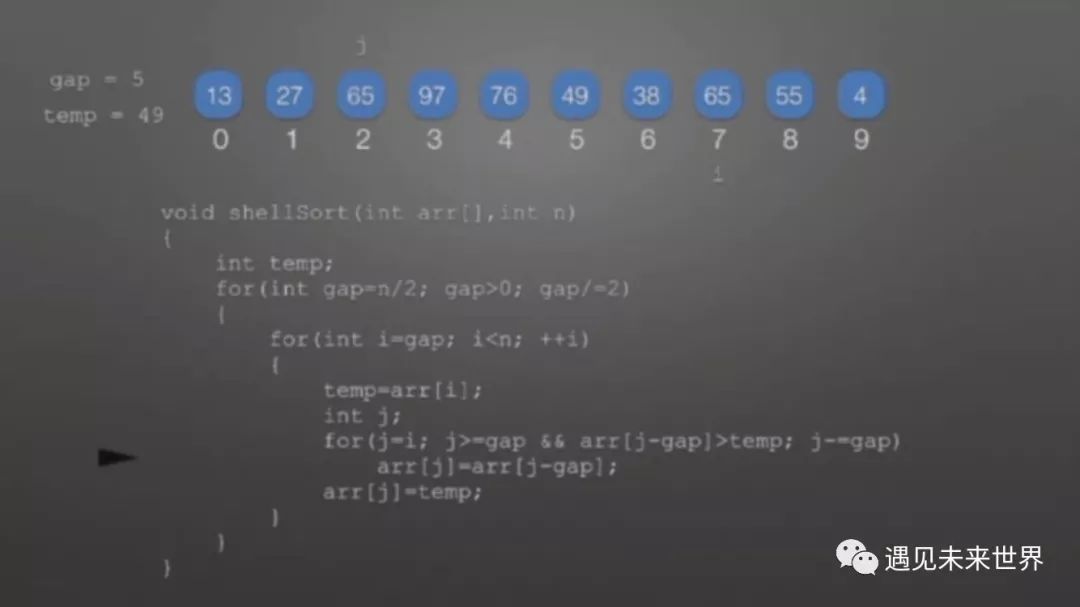这里比较后完成元素的交换。
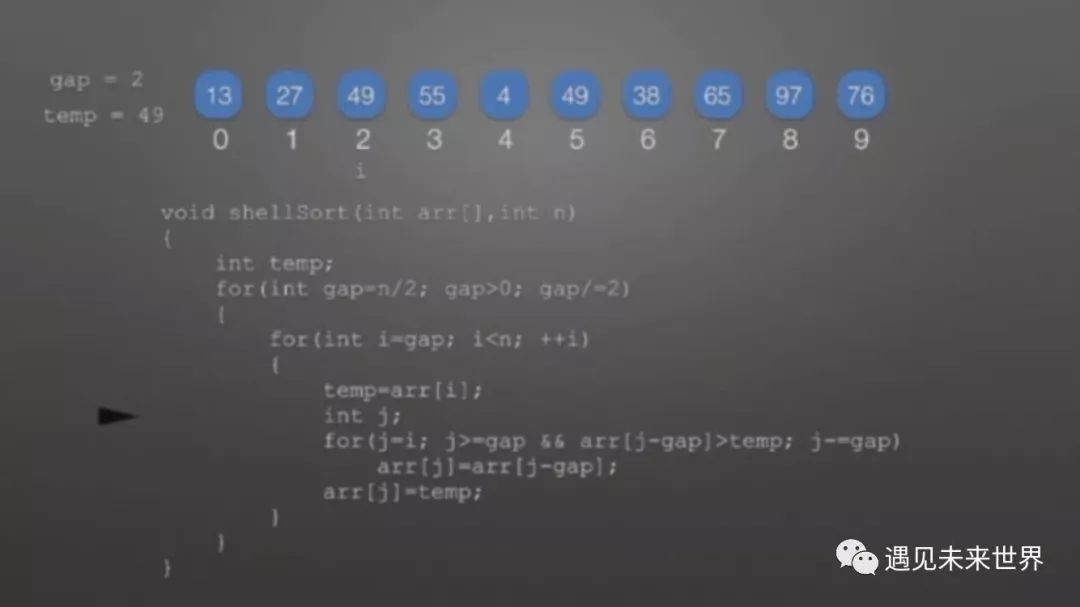gap=5结束，接下来进行gap=2的循环
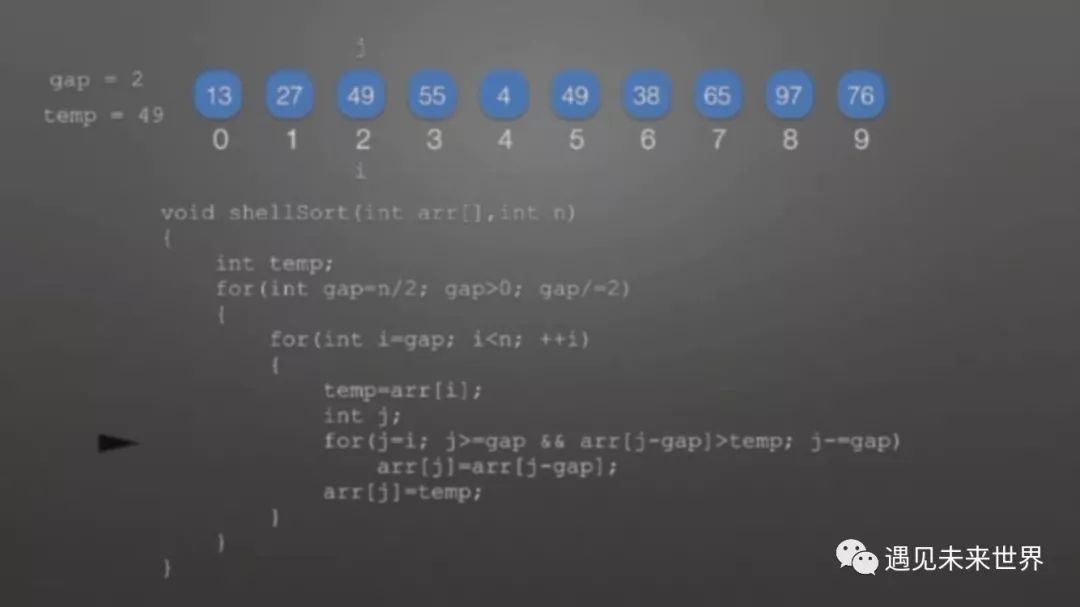gap=2，i=2时，这里不需要交换。
所以这里的arr【j】=temp并未进行任何操作。
同理，依次类推，完成数组的排序，希尔排序就此完成。
今天对于希尔排序暂时总结到这里，希尔排序相对排序变得也稍微复杂一点，see you later！！！
以上是关于浅谈复杂排序之希尔排序！的主要内容，如果未能解决你的问题，请参考以下文章