十分钟学会一个算法：希尔排序

Posted 2021-04-25 猿是一家

上一篇：。

昨天有介绍过直接插入排序是如何实现的 ><，今天我们一起来看看十大排序算法之 -- 希尔排序是如何实现的。

希尔是个什么鬼？

排个序为啥叫这名字？

额。人家是人不是鬼，全名叫：Donald Shell，该排序算法在1959年由这哥们提出，最后用其名字命名了而已。

算法由来

话说某一个夜深人静的夜晚，shell独坐在实验室码着代码。在码到排序算法时，他发现两个现象：

1. 直接插入排序的复杂度强依赖输入数据的序列：如果一个序列逆序时，复杂度是O(n^2)，而如果正序时，复杂度可提高到O(n)。

2. 在输入数据量较小时，直接插入排序算法效率还挺高。

于是这哥们就开始异想天开：是不是可以先将待排序列切分成多个小序列，然后在这些小序列内进行排序，排完后再整合在一起，再作一次直接插入排序。

说完他就干了起来，经过那一夜无眠之后，他码完了这个新程序，发现复杂度的确有牛逼那么一点点。于是赶紧给这个牛逼的算法取上了自己的名字。

算法思想

先将整个待记录序列分割成若干个子序列，对这些子序列分别进行直接插入排序，待整个序列中的记录基本有序时，再对全体记录进行一次直接插入排序。

拆分后包含三个步骤：

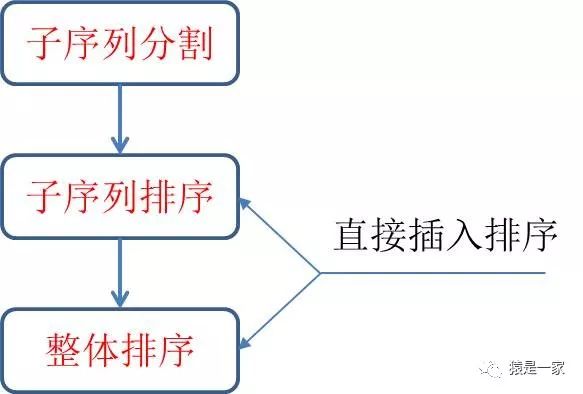
后两个步骤内还是用的直接插入排序进行的排序。所以它其实是一个改良的直接插入排序算法。

算法流程

该算法可分解成如下流程实现：

1. 确定一个正整数d1 （d1<n)，把所有序号相隔d1的数组元素放一组，组内进行直接插入排序；

2. 取d2 (d2<d1)，重复上述分组和排序操作；

3. 直至di=1，即所有记录放进一个组中排序为止。

上面的文字不太好理解，有点云里雾里，通过下面这个动画再详细介绍下：

排序序列：4，5，3，2，1

选取d=2，分割成两个子序列：[4,3,1] 和 [5, 2]

对子序列排序后为：[1, 3, 4] 和 [2, 5]

最后合并排序成正序

c代码实现如下：

//根据当前增量进行插入排序void shellInsert(int array[],int n,int dk){ int i,j,temp; for(i=dk;i<n;i++)//分别向每组的有序区域插入 { temp=array[i]; for(j=i-dk;(j>=i%dk)&&array[j]>temp;j-=dk)//比较与记录后移同时进行 array[j+dk]=array[j]; if(j!=i-dk) array[j+dk]=temp;//插入 }}

算法疑问

上面的流程中我们有使用到分割间距d，那我们是如何确定这值的呢？

其实这个问题不仅仅是数学问题，也直接关系到希尔排序复杂度，然而，到目前为止还未有人求得一种好的增量序列以达到最优的复杂度。

结语

看过该算法的逻辑之后我们会发现希尔排序其实是一变种的直接插入排序，其实它还有另外一个名字：缩小增量排序。似乎缩小增量排序会更贴合算法的流程，可谁叫Shell这哥们名气大呢。

﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌﹌

原是一家，共同成长