希尔排序过程始末

Posted 2021-04-25 奇妙的coco

---

【1】

有关插入排序

---

1，插入排序的基本方法是：每步将一个待排序的元素，按其排序码大小插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为止。

2，可以选择不同的方法在已经排好序的有序数据表中寻找插入位置，依据查找方法的不同，有多种插入排序方法。下面是常用的三种。

• 直接插入排序

• 折半插入排序

• 希尔排序

3，直接插入排序基本思想：当插入第i（i>1）个元素时，前面的data[0]，data[1]，……，data[i-1]已经排好序。这时用data[i]的排序码与data[i-1]，data[i-2]，……的排序码顺序进行比较，找到插入位置即将data[i]插入，原来位置上的元素向后顺序移动。
4，折半插入排序基本思想：设元素序列data[0]，data[1]，data[n-1]。其中data[0]，data[1]，……，data[i-1]是已经排好序的元素。在插入data[i]时，利用折半搜索法寻找data[i]的插入位置。

5，希尔排序过程相比前两种有些不同,下面我们主要介绍希尔排序过程的实现。

---

【2】
希尔排序

---

1，希尔排序（shell's sort）这个排序方法又称为缩小增量排序，是1959年D.L.Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。
2，由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。
3，希尔排序举例：

（1）下面给出一个数据列：

（2） 第一趟取increment的方法是：n/3向下取整+1=3（关于increment的取法之后会有介绍）。将整个数据列划分为间隔为3的3个子序列，然后对每一个子序列执行直接插入排序，相当于对整个序列执行了部分排序调整。图解如下：

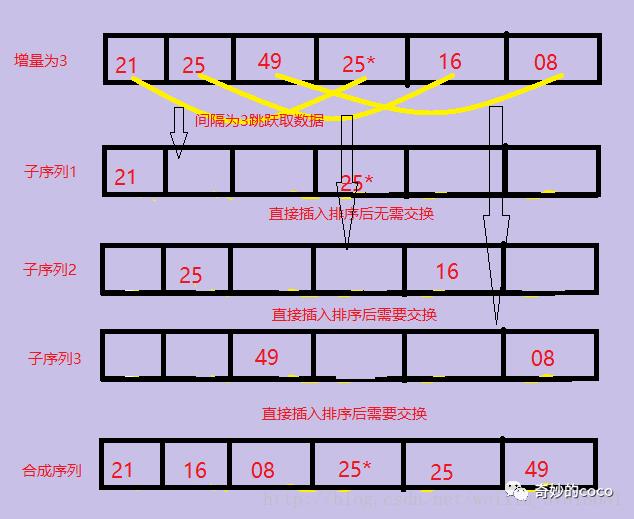
（3）第二趟将间隔increment= increment/3向下取整+1=2，将整个元素序列划分为2个间隔为2的子序列，分别进行排序。图解如下：

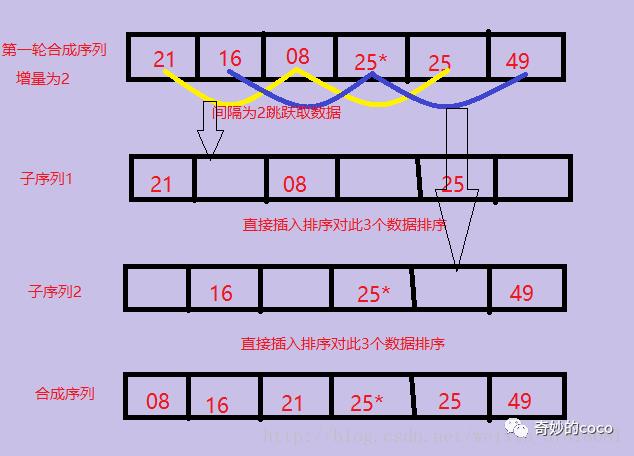
（4）第3趟把间隔缩小为increment= increment/3向下取整+1=1，当增量为1的时候，实际上就是把整个数列作为一个子序列进行插入排序，图解如下：

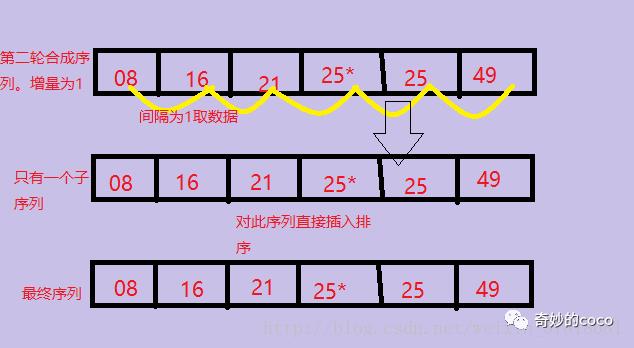
（5）直到increment=1时，就是对整个数列做最后一次调整，因为前面的序列调整已经使得整个序列部分有序，所以最后一次调整也变得十分轻松，这也是希尔排序性能优越的体现。

4，希尔排序算法的代码实现（C++）

//函数功能，希尔排序算法对数字递增排序//函数参数，数列起点，数列终点void shell_sort(const int start, const int end) { int increment = end - start + 1; //初始化划分增量 int temp{ 0 }; do { //每次减小增量，直到increment = 1 increment = increment / 3 + 1; for (int i = start + increment; i <= end; ++i) { //对每个划分进行直接插入排序 if (numbers[i - increment] > numbers[i]) { temp = numbers[i]; int j = i - increment; do { //移动元素并寻找位置 numbers[j + increment] = numbers[j]; j -= increment; } while (j >= start && numbers[j] > temp); numbers[j + increment] = temp; //插入元素 } } } while (increment > 1);}

上面的函数的第一个do……while控制increment每次的缩小，其内部便是直接插入排序算法的使用，与直接插入排序算法稍有不同的一点是：其j每次的变化量是increment而不是1。
5，关于希尔排序increment（增量）的取法。
增量increment的取法有各种方案。最初shell提出取increment=n/2向下取整，increment=increment/2向下取整，直到increment=1。但由于直到最后一步，在奇数位置的元素才会与偶数位置的元素进行比较，这样使用这个序列的效率会很低。后来Knuth提出取increment=n/3向下取整+1.还有人提出都取奇数为好，也有人提出increment互质为好。应用不同的序列会使希尔排序算法的性能有很大的差异。
6，希尔排序应该注意的问题
从上面图解希尔排序的过程可以看到，相等的排序码25在排序前后的顺序发生了颠倒，所以希尔排序是一种不稳定的排序算法。

---

【3】

关于希尔排序的性能分析

---

1，对希尔排序的时间复杂度分析很困难，在特定情况下可以准确的估算排序码的比较次数和元素移动的次数，但要想弄清楚排序码比较次数和元素移动次数与增量选择之间的依赖关系，并给出完整的数学分析，还没有人能够做到。

2，这里我们把3种常用的插入排序做一个程序测试，通过每种算法测试所执行的时间，来定性的认识希尔排序的性能优劣。测试的思路是通过生成1000个1——1000之间的随机数，令三种排序算法分别对其进行排序，输出排序所花费的时间。

3，测试的程序源码（C++）

/** 插入排序算法*/#include <iostream>#include <vector>#include <string>#include <ctime>using namespace std;
//vector<int> numbers{3, 2, 4, 6, 1, 9, 5, 8, 7, 10};//vector<int> numbers{72, 6, 57, 88, 60, 42, 83, 73, 48, 85};//vector<int> numbers{21, 25, 49, 25, 16, 8};vector<int> numbers;
//函数功能，直接插入算法对数字排序//函数参数，数列起点，数列终点void dinsert_sort(const int start, const int end) { for (int i = start + 1; i <= end; ++i) { if (numbers[i] < numbers[i - 1]) { int temp = numbers[i]; int j = i - 1; do { //依次移动并寻找插入位置 numbers[j + 1] = numbers[j]; --j; }while (j >= start && numbers[j] > temp); numbers[j + 1] = temp; //插入元素 } }}
//函数功能，折半插入算法对数字排序//函数参数，数列起点，数列终点void binsert_sort(const int start, const int end) { int low = 0, high = 0, middle = 0; for (int i = start + 1; i <= end; ++i) { int temp = numbers[i]; low = start; high = i - 1; while (low <= high) { //折半搜索寻找插入位置 middle = (low + high) / 2; if (numbers[middle] > temp) {  high = middle - 1; //定位到前半部分 } else { low = middle + 1; //定位到后半部分 } } for (int k = i - 1; k >= low; --k) { numbers[k + 1] = numbers[k]; //成块移动，空出插入位置 } numbers[low] = temp; //插入元素 }}
//函数功能，希尔排序算法对数字递增排序//函数参数，数列起点，数列终点void shell_sort(const int start, const int end) { int increment = end - start + 1; //初始化划分增量 int temp{ 0 }; do { //每次减小增量，直到increment = 1 increment = increment / 3 + 1; for (int i = start + increment; i <= end; ++i) { //对每个划分进行直接插入排序 if (numbers[i - increment] > numbers[i]) { temp = numbers[i]; int j = i - increment; do { //移动元素并寻找位置 numbers[j + increment] = numbers[j]; j -= increment; } while (j >= start && numbers[j] > temp); numbers[j + increment] = temp; //插入元素 } } } while (increment > 1);}
//函数功能，随机产生amount个start——end内的随机数并存入指定容器//函数参数，随机数范围起点，随机数范围终点，随机数生成数量void produceRandomNumbers(const int start, const int end, const int amount) { srand((unsigned)time(NULL)); for (int cnt = 1; cnt <= amount; ++cnt) { numbers.push_back(start + (rand() % (end - start))); }}

int main(){ time_t c_start, c_end; produceRandomNumbers(1, 1000, 1000);
 c_start = clock(); //dinsert_sort(0, 999); //binsert_sort(0, 999); shell_sort(0, 999); c_end = clock();
 cout << "当前排序算法花费时间为：" << difftime(c_end, c_start) << "ms" << endl; for (auto iter = numbers.cbegin(); iter != numbers.cend(); ++iter) { cout << *iter << " "; }
 system("pause"); return 0;}

4，有关测试结果

直接插入排序：

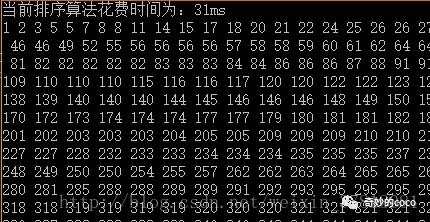
折半插入排序：

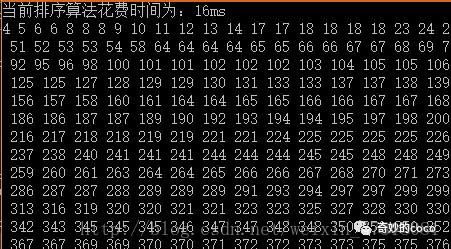
希尔排序：

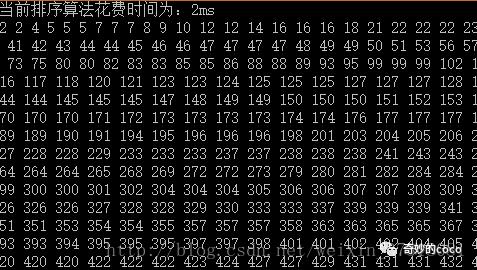
当然这里没有让其对同一组数据进行测试，会存在一定的误差，但是通过对其多次测试，3中算法的平均优劣程度还是比较明显的。

---

【4】

写在最后

---

关于数字的排序算法的研究是一个乐此不疲的话题，对于这些基本的排序算法应该常记、常用。也希望大家对文中不当之处给予指正。

参考资料：《数据结构C++语言描述》殷人昆/相关博文

---

编辑：coco

封面：coco

之后等于永不

如果有收获，那我就太开心了，如果你分享给了其他人，那就更好了。

奇妙的coco