面试之希尔排序——她也阔以优化！！！

Posted 2021-04-25 大数据修行直通车

进入公众号点击“学习资源”，加入大数据群，获取各类技术资料

排序算法4 希尔排序

课代表总结

借鉴昨天推文插入排序的思想，优化之后的移位希尔排序法，目前来看效率是最高的！一直强调，算法无论简单与否，进行优化的思考过程是最重要的！

最基本概念

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个数组排序完成。

基本思路

首先希尔排序是插入排序的升级版。例如arr[6]={2,3,4,5,6,1}数组要进行最后一趟排序，即要将最后一个元素1移到数组的第一个位置arr[0];如果数组的长度过大，那么使用插入排序算法代价很大。

基于如上的痛点，提出希尔排序，希尔排序使用分而治之的思想。即首先将整体数组分为grep=arr.length/2个小组，分组时每隔一个步长（这里步长设置的为grep）取一个数据，而不是相邻的数据，在每一个小组中进行插入排序。

完成上一步操作，再将整体原始的数组分为  grep =（arr.length/2)/2 组，继续在组内进行插入排序，直到 grep <= 0这样的操作会将较小的值移动到数组的前半部分，而较大的值移动到数组的后半部分，有效的避免了上述的情况。

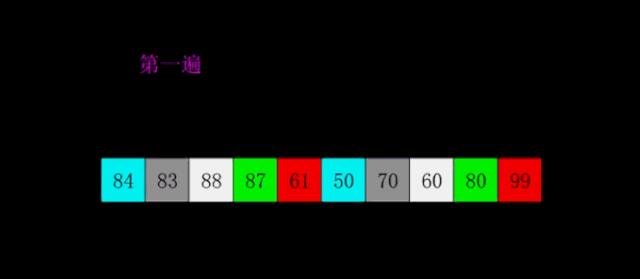
「举例说明」

例如待排序数组为

arr[10]={8,9,1,7,2,3,5,4,6,0}

1、首先将数组分为 arr.length/2=5 个小组，即设 arr.length/2=5 为步长 grep.

2、在数组中每隔一个grep取一个数值，组成一个小组，即待排序数组分为5组，分别为{8,3}，{9,5}，{1,4}，{7,6}，{2,0}。

3、在组内进行排序，排序之后的数组为 arr={3,5,1,6,0,8,9,4,7,2}。

4、继续将数组分为 (arr.length/2)/2=2 组，按照上面的步骤，分组情况为{3,1,0,9,7}，{5,6,8,4,2}.

5、小组内分别进行排序，排序之后数组的结果是arr={0,2,1,4,3,5,7,6,9,8}。

6、再继续将数组分为 (arr.length/2/2)/2=1 组，即整个数组为一组，进行排序，排序结果为 {0,1,2,3,4,5,6,7,8,9}，排序完成。

「算法思想」

1）算法每次需要隔一个步长取一个数值，并将其作为一组进行排序，在分组时，可以从每个小组的最后一个数值往前取，例如临时变量i=grep，arr[i]就是第1组的最后一个元素，arr[i-grep]是第1组的倒数第二个元素，直到i-grep<0，说明本组元素全部取完。这样可以避免数组出界。

2）希尔排序是一种不稳定的排序方式，平均时间复杂度为0(nlogn),最坏情况的时间复杂度是O(n^s)(1<s<2)。

「代码实现」

在进行组内排序时有两种方法：（1）交换法（2）移位法

「交换法代码实现：」

【交换法】和前天推文冒泡排序思想类似，当分组内发现逆序的数值时，进行交换。

public class Shellsortb { public static void main(String[] args) { int[] arr = new int[] {8,9,1,7,2,3,5,4,6,0}; shellsort2(arr); System.out.println(Arrays.toString(arr)); } public static void shellsort2(int[] arr) { int temp=0; for(int grep=arr.length/2;grep>0;grep=grep/2) { //grep 为每次分的组数 for(int i=grep;i<arr.length;i=i+1) { for(int j=i-grep;j>=0;j=j-grep) { if(arr[j]>arr[j+grep]) { //冒泡排序的思想 temp=arr[j]; arr[j]=arr[j+grep]; arr[j+grep]=temp; }  } } System.out.println(Arrays.toString(arr)); } }}

「移位法代码实现」

【移位法】借鉴插入排序的思想（想象你斗地主时候如何排牌），插入排序和冒泡排序的思想，可以翻看前两天的推文，每篇都写的很清楚，也都有相应的优化。

public class Shellsort1 { public static void main(String[] args) { int[] arr = new int[] {8,9,1,7,2,3,5,4,6,0}; shellsort(arr); System.out.println(Arrays.toString(arr));  } public static void shellsort(int[] arr) { int temp; for (int grep = arr.length / 2; grep > 0; grep = grep / 2) { for (int i = grep; i < arr.length; i++) {//应该比较熟悉了，上一篇推文中插入排序的思想 int j = i; // i为插入排序中待插入数组的下标 temp = arr[j]; // temp保存待插入的数值，防止后续的移动覆盖原来的数值 while (j - grep >= 0 && temp < arr[j - grep]) { arr[j] = arr[j - grep]; // 在每一个小组中进行步长为grep的插入排序 j = j - grep; } arr[j] = temp; } } }}

性能分析

随机产生80000个数据，进行从小到大排序。测试时间运行结果图为：

希尔交换法：

交换法

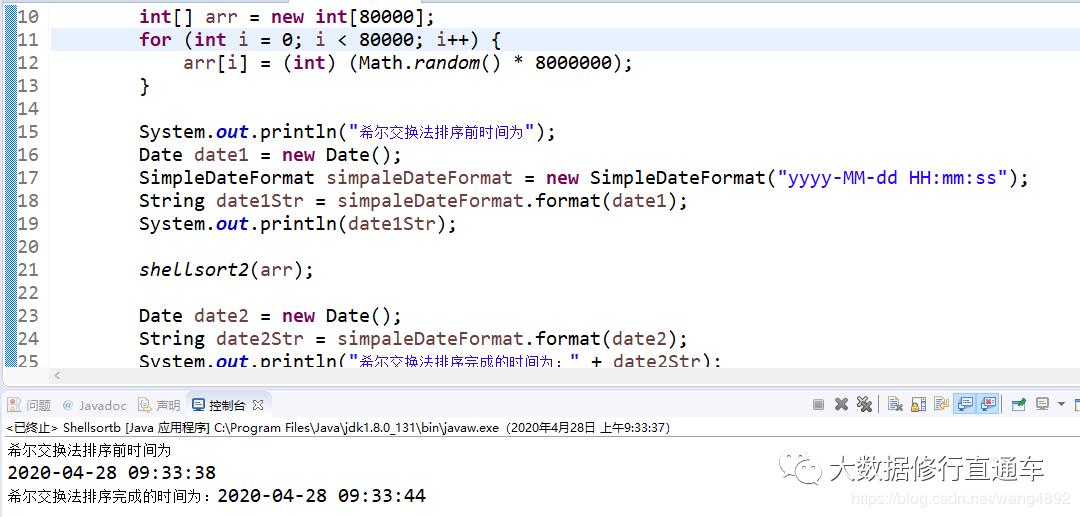
希尔移位法：

移位法

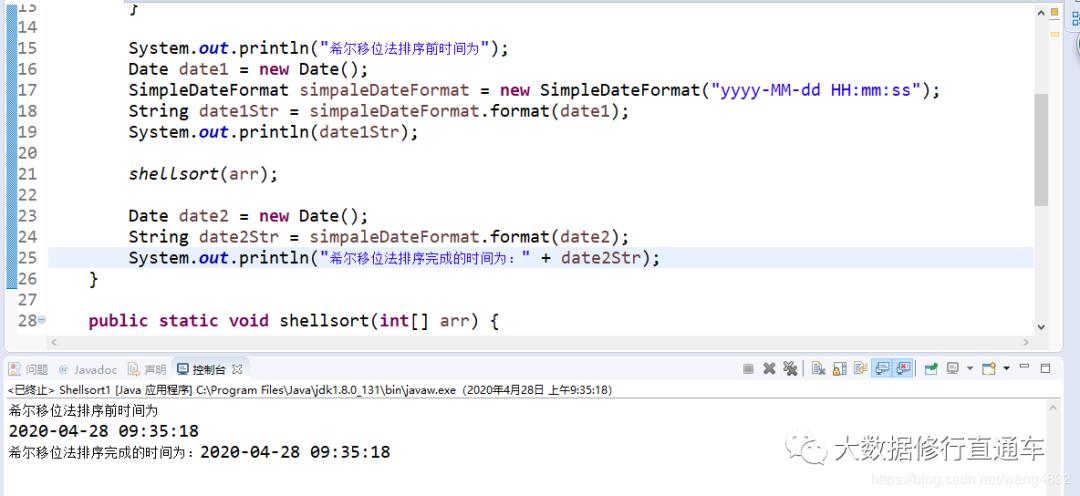
随机产生80000个数据进行排序，各个算法所用时间对比我做了个表。

排序方法	使用时间
冒泡排序	12秒
选择排序	1秒
插入排序	3秒
希尔排序（交换）	6秒
希尔排序（移位）	小于1秒

总结

• 通过上述的对比，各个算法的效率显而易见。希尔排序的交换法并没有优化原始的插入排序，从此也可以看出 冒泡排序的效率是非常低的。【diss一波最传统的冒泡hhh】 随机产生800000（上述是80000提高了十倍）个随机数进行排序，希尔排序的移位法只需要2秒左右的时间，因此可以看出希尔排序（移位法）优于插入排序。
• 当然这些都是次要的， 排序算法都不难，最主要的是优化的思想！ 工作中也是这样，代码简单难的是优化。
• 无论简单的算法还是更为复杂的，主要是 解决问题的思路，举一反三，多思考 ，很多地方都可以应用的到！

PS: 笔者建了个学习交流群，禁广告、推广，大家有啥问题也可以在群里提问，有需要的小伙伴可以加一下~

加群方式 - 扫描下方

以上是关于面试之希尔排序——她也阔以优化！！！的主要内容，如果未能解决你的问题，请参考以下文章

面试之希尔排序

排序算法之希尔（优化冒泡）排序

《糊涂算法》之八大排序——希尔排序

挖掘算法中的数据结构：O(n^2)排序算法之 选择插入冒泡希尔排序 及 优化

十大排序之希尔排序

排序之希尔排序