插入类排序—(折半)插入排序希尔排序

Posted 2021-04-25 bigsai

前言

在数据结构和算法中，排序是非常重要的一环，并且排序也是渗透编程的方方面面。

你或许在写一个sql的order by按照某组进行排序，又或者你在刷一道题时候、常常遇到贪心+自定义排序求解的思路题，或者变态的面试官让你手写快排，又或者是app的姓氏升降序列 - - -

然而在实际的排序算法的实现上，方式是众多的，不同算法对不同的特征数据的效率也是不同的，并且不同算法的时间复杂度、空间复杂度也不同。

对于排序，一般认为有八大排序(也有九大)。但是在分配的大类中，我们常常分为 基于插入排序(插入排序、希尔排序)；基于交换的排序(冒泡排序、快速排序)；基于选择的排序(简单选择排序、堆排序)，归并排序和基数排序。

插入排序

在这里插入图片描述

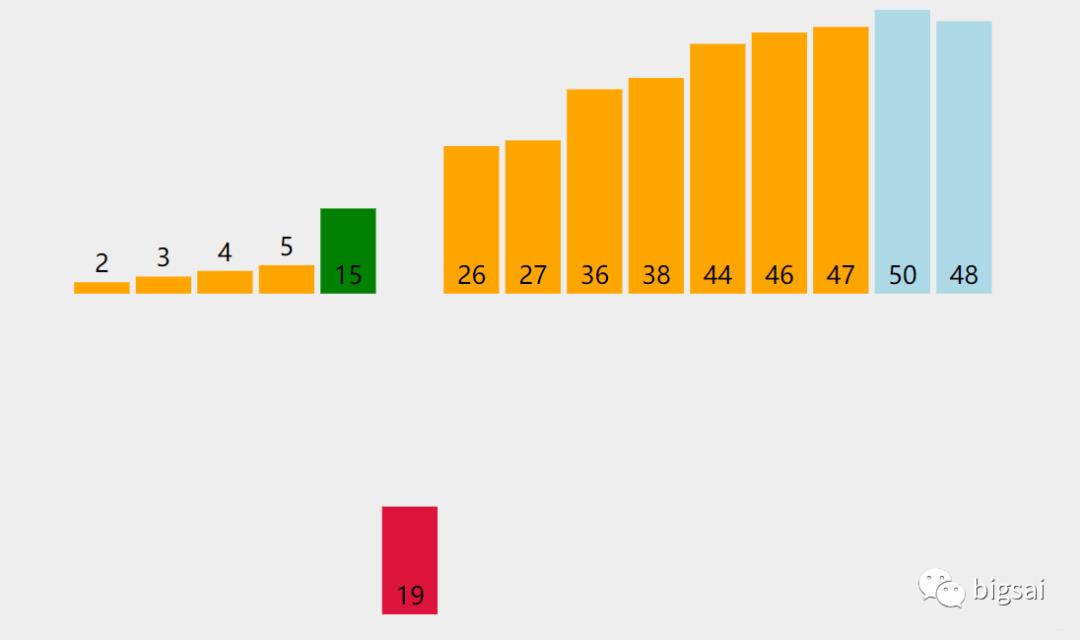
插入排序在所有排序算法中的思想算得上是最简单的了。和我们上学时候 从前往后、按高矮顺序排序。那么，一堆高低无序的人群中，从第一个开始，如果前面有比自己高的，就直接插入到合适的位置。一直到队伍的最后一个完成插入整个队列才能满足有序。

虽然在思想上是很简单的，或许你认为它的实现、次数也很简单，每个同学插入到合适的位置就好了。但事实你这么想错了。你实质一眼看到确切的位置在脑海中已经默默经过pass、pass、pass。。。计算机每次只能进行一次计算，所以每个他要确定他要插入到那，他必须一个一个往前比较。所以这个时间复杂度是O(n2)的。如果数据很大的话其实效率还是很低的。

插入排序的具体步骤：

• 从第一个开始选取数据

• 从这个点和前面的比较，一直找到第一个小于自己的或者是到首位

• 插入到对应位置，重复第一步从下一个元素继续。

在这里插入图片描述

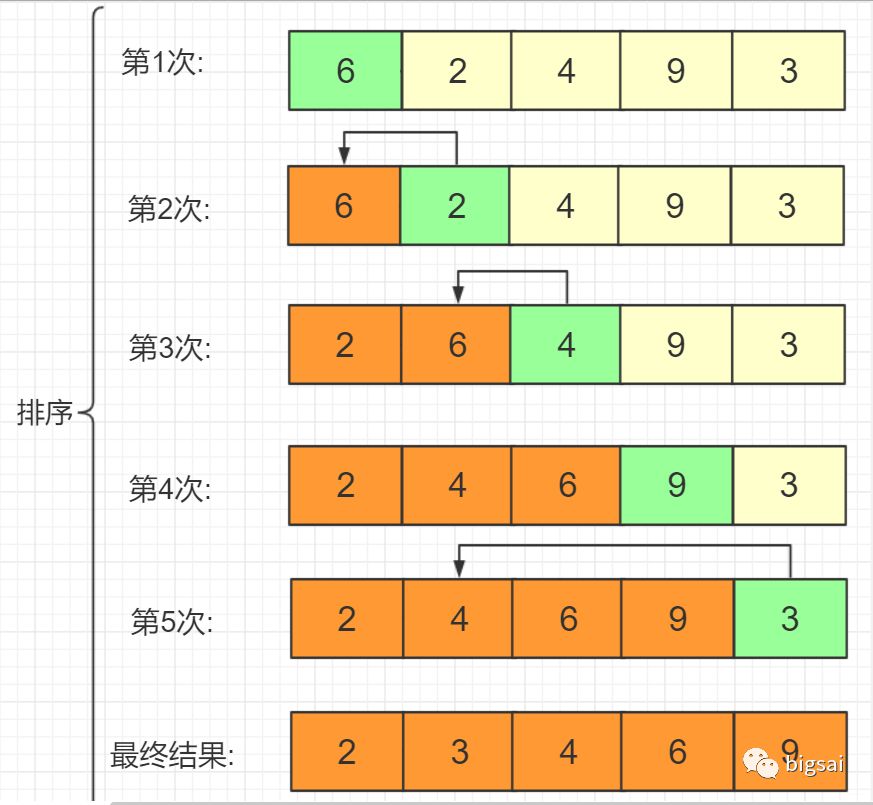
在具体实现上有以下的需要注意：

• 算法更适合链表，因为链表的插入删除更简单

• 对于数组的插入，具体就是该元素代替被插入的位置，被插入以及后面元素全部后移一位(事实上这个顺序表插入开销挺大的，不太友好)

• 这个插入排序如果使用数组的话我们实质上是用数组的多次交换而达到插入的效果。具体可以参考前面数据结构的顺序表专栏！

  至于数组的头节点是怎么回事呢？因为你需要 在插入后面全部后移。我们为了减少计算，在每次比较的时候直接交换后移。用一个临时变量储存该元素。而带头节点就是第0个不用。把第0个当作临时空间。同时也不需要判断是否等于0.因为0位置元素一定小于等于要插入元素。到这里可以直接插入！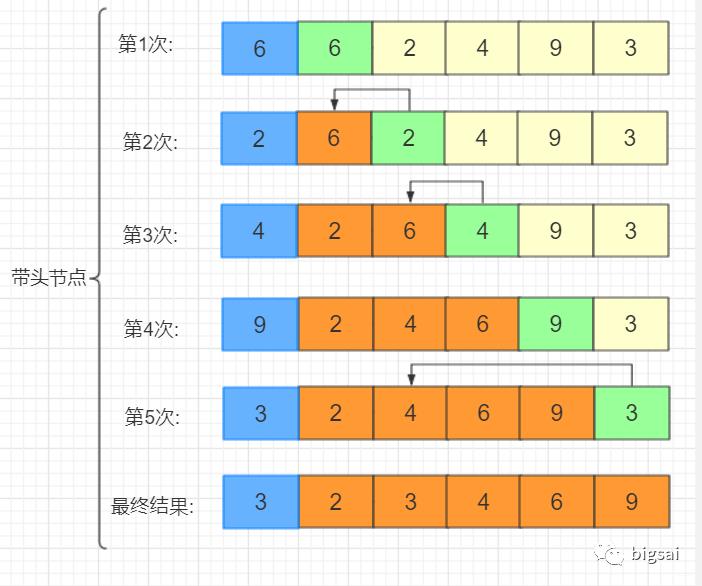
  

  

  在这里插入图片描述

  
  插入排序更适合链表，减少挪动的次数,只需考虑比较次数然后插入。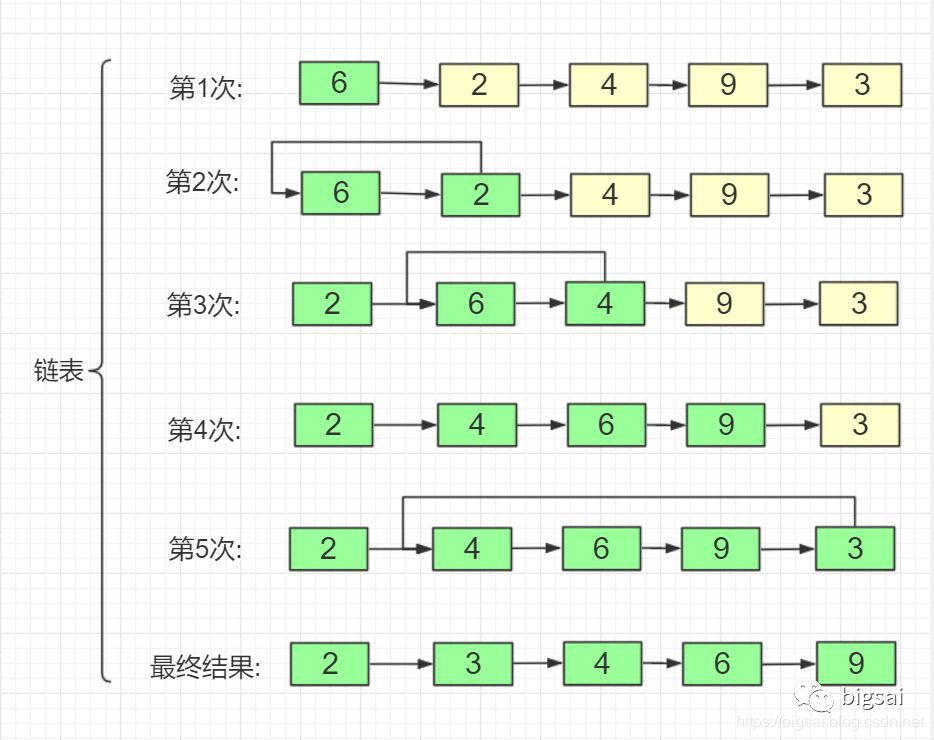
  

  

  在这里插入图片描述

  
  插入排序实现的代码为：

  
  

折半插入排序

折半插入排序和插入排序有什么关联？
首先，折半插入排序的本质依然是插入排序，仅仅是对插入排序进行了部分优化。而优化的部分就是向前查找比较的部分。其实它就是将查找从暴力枚举一一遍历变为二分查找。

在这里插入图片描述

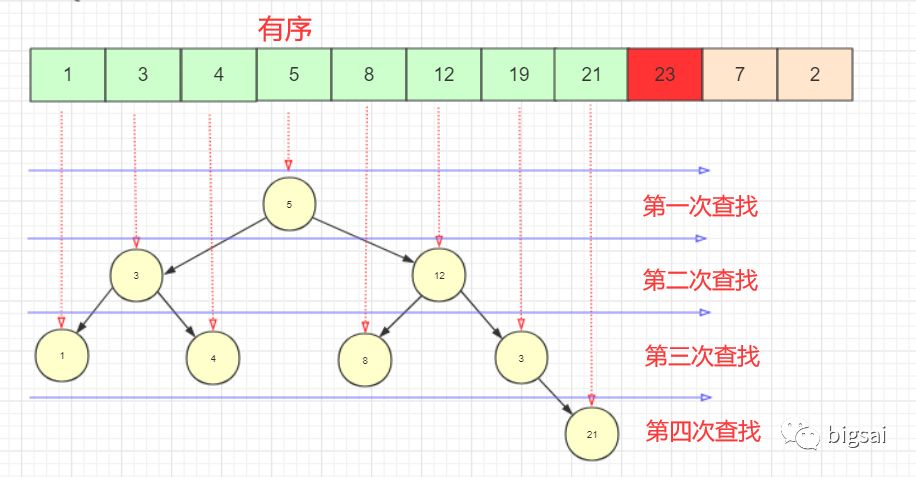
对于二分查找，这里不做详细介绍，我将在另一篇博文中再做详细介绍，因为没进行一次插入，前面的序列都是有序的。如果序列很长的话，那么一个个查找比较可能会占用过多的次数。而我们从序列中间试探二分夹逼的话可以用log级别完成查找。序列越长那么查找减少的次数就越多。

当然很遗憾的是，折半插入虽然可以降低查找次数，但是无法改变整个算法的时间复杂度(数组实现)。因为在每个元素的插入过程中，虽然查找可以降到log'n，但是在顺序表的向前移动交换依然还是得一个一个移动啊。折半插入可以理解为对于每个位置的平均时间复杂度从O(N)查找+O(N)交换移动变成O(logN)查找+Ｏ(n)交换移动。所以，整个时间复杂度依然是Ｏ(n2).但是，别太小看那点优化，在数据大、链式存储的情况下其实还是节省很大时间的！

希尔排序

因为上述的基于排序的算法中大部分都是适合于数据量不大、或者有序的情况才能达到较好的效果。无数牛逼的人物在不断想方设法的优化和解决这个难题。终于，有个叫希尔的牛逼人物终于研究出来一种排序算法——希尔排序。考虑到了数据量和有序性两个方面纬度来设计算法。同时，希尔排序是一组插入排序的组合。百科如下定义：

希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法.
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。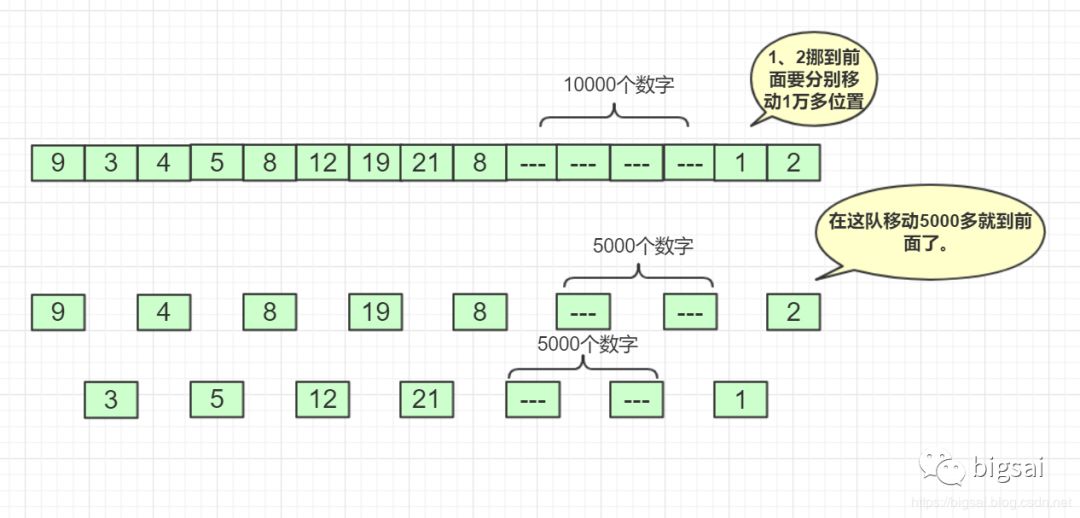

在这里插入图片描述

首先插入排序在两个情况下效率还可以。

1. 有序序列，因为如果有序的话每个元素很容易找到前面一直比自己大的几个或0个元素，这种情况时间复杂度比现行级别稍微高那么一丢丢。

2. 元素较少。你强任你强，很少的元素再怎么平方在计算机面前也是小菜。

在这里插入图片描述

而希尔排序刚好巧妙的运用，分割。利用了上面的优点。对于一个长串，希尔首先将序列分割(非线性分割)而是按照某个数模(取余这个类似报数1、2、3、4. 1、2、3、4)这样形式上在一组的分割先降低长度分别进行插入排序,这样很小的数在后面可以通过较少的次数移动到相对考前的位置。然后慢慢合并变长，再稍稍移动。。。。。因为每次这样小插入都会使得序列变得更加有序，稍微有序序列执行插入成本并不高。所以这样能够在合并到最终的时候基本小的在前，大的在后。这样希尔排序下来一般还是能够减少很多时间的。

前面的分组取余相当于按照这个规则预处理。到最后一次就变得很有大小规则了(至少奇偶数分别有序)，这样整个插入排序的复杂度大大降低，很少出现需要移动很大幅度的数字。

虽然希尔排序看起来多了那么几次排序。但是在数据较长的串面前多几次比起平方指数级别还是弟弟的。虽然希尔排序的证明是个问题，并且分割的取值也并没有理论证明最好。但是一般从n/2一直到1.马克思曾说：实践是检验真理的唯一标准。实践检验它好它就是好！

实现代码

package 八大排序;

import java.util.Arrays;

public class 直接插入 {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int a[]= {21,25,8,7,45,2,8,18,9,88,3};
        int b[]=new int[10];
        a=insertsort(a);
        System.out.println(Arrays.toString(a));
        System.out.println();
        b=shellsort(a);
        System.out.println(Arrays.toString(a));
    }

    static int [] insertsort (int a[])
    {
        int team=0;
        for(int i=1;i<a.length;i++)
        {
            System.out.println(Arrays.toString(a));
            team=a[i];
            for(int j=i-1;j>=0;j--)
            {

                if(a[j]>team)
                {
                    a[j+1]=a[j];
                    a[j]=team;  
                }   
                else {
                    break;
                }
            }
        }
        return a;       
    }
    static int [] shellsort (int a[])
    {
        int d=a.length;
        int team=0;//临时变量
        for(;d>=1;d/=2)
        for(int i=d;i<a.length;i++)
        {

            System.out.println(Arrays.toString(a));
            team=a[i];
            for(int j=i-d;j>=0;j-=d)
            {               
                if(a[j]>team)
                {
                    a[j+d]=a[j];
                    a[j]=team;  
                }
                else {
                    break;
                }
            }
        }
        return a;       
    }

}

输出结果：

[21, 25, 8, 7, 45, 2, 8, 18, 9, 88, 3]
[21, 25, 8, 7, 45, 2, 8, 18, 9, 88, 3]
[8, 21, 25, 7, 45, 2, 8, 18, 9, 88, 3]
[7, 8, 21, 25, 45, 2, 8, 18, 9, 88, 3]
[7, 8, 21, 25, 45, 2, 8, 18, 9, 88, 3]
[2, 7, 8, 21, 25, 45, 8, 18, 9, 88, 3]
[2, 7, 8, 8, 21, 25, 45, 18, 9, 88, 3]
[2, 7, 8, 8, 18, 21, 25, 45, 9, 88, 3]
[2, 7, 8, 8, 9, 18, 21, 25, 45, 88, 3]
[2, 7, 8, 8, 9, 18, 21, 25, 45, 88, 3]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
空格
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]
[2, 3, 7, 8, 8, 9, 18, 21, 25, 45, 88]