插入排序的故事

Posted 2021-04-25 Python算法之旅

话说计算机世界有一个诚实国，那里的人们不但诚实，而且尊老，每次排队都让年纪大的人排前面。

有一次小胖到诚实国去旅游，肚子饿了想吃东西，发现一个烧饼店门前有人排着队，他就跟在队伍后面一起排队。没过多久，又来了一个人，站在小胖后面，并问他：“小伙子，你今年多大？”

“26，怎么啦？”

“26？那你得排在我后面，我今年38啦。”

“为什么？明明是我先来的，先来后到你不懂吗？”

“哈哈，先来后到？小伙子你是外地来旅游的吧，还不知道我们这的规矩。我们诚实国人不仅诚实，而且尊老，排队都让年纪大的人排前面。我比你大，所以要排在你前面。”

“原来是这样！对了，在我前面是一个小孩，那我也可以先插到他前面去咯？”

“是的，你先往前面插队，等你弄好了，我再来。”

“还有这种神操作！谢谢你提醒我啊！我要向前去了。”

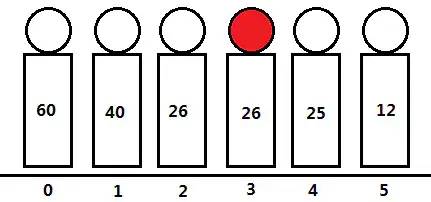
此时小胖所站位置如图示：(地面下方的序号表示每个人所在的位置，用0-5表示；人体身上的数字表示其年龄。红脸的是小胖，他26岁，站在5号位置)

小胖拍了拍前面少年的肩膀，问他：“小朋友，今年几岁了？”

“叔叔，我今年12岁。”

“那请你让一让，叔叔我今年26了。”

“好的。”

于是二人换了位置。此时站在小胖前面的是一个瘦瘦高高的年轻人，戴着一副眼镜，小胖也吃不准他有多大年纪，就小心翼翼地问他：“兄弟我今年26，请问你多大了？”

“25”，瘦子一边回答一边默默地站到小胖后面去了。

此时站在小胖前面的是一个跟他长得差不多的胖墩，小胖热情地和他打招呼：“嗨，兄弟，哥哥我今年26，你呢？”

“26啊？那跟在我后面吧，哥哥我今年也正好26岁。”

此时小胖所站位置如图示：

如果我们用Python语言描述小胖插队的过程，应该是这样：

lst = [60,40,26,25,12,25]#小胖插队前的站队情况age = 26 #小胖的年龄pos = 5 #小胖的初始位置序号while pos > 0: #不断询问前面的人，直到到达队伍前端 if lst[pos-1] < age: #若前面的人比小胖小，则后退一位（相当于和小胖交换了位置） lst[pos] = lst[pos-1] pos -= 1 #继续向前询问下一个人 else: #否则说明小胖找到了正确的插队位置，退出循环 breaklst[pos] = age #最终小胖站在正确的位置上print(lst) #输出小胖插队后的站队情况

几个月后，小胖带着女朋友花花一起去诚实国旅游，来到同一家店排队买烧饼。正逢黄金周旅游旺季，排队的人可真多啊！花花看看前面长长的队伍，又看了看空空的矿泉水瓶，对小胖撒娇说：“亲爱的，伦家的水喝光了，口干舌燥，不想费口舌和前面的人比谁大谁小。反正你也知道我只比你大3岁，要不你帮我去问，找到正确的位置后，站在那人旁边，给我发个信号，然后我叫前面的人给我挪出位置，就可以直接走过去了。用Python语言表示就是这样。”

#将值为age的元素插入到非递增列表lst中，并保持列表的有序性def insert(lst,age): pos = insert_pos(lst,0,len(lst)-1,age) #小胖帮花花查找插队的位置 lst.append(age) #花花先站在队伍的后面，使得列表的长度加1 for i in range(len(lst)-1,pos,-1):#人们逐个后移，为花花腾出插入位置 lst[i] = lst[i-1]    lst[pos] = age #最终花花站在正确的位置上

“知道了，不就是帮你找到正确的插入位置吗。没问题，看我的。”

小胖去了，他很卖力气，逐个询问排队人的年龄。半个小时过去了，小胖还在问，花花等得有些不耐烦了。又过了十几分钟，小胖终于在远处朝花花挥手了，花花知道他已经找到正确位置了。于是花花依次跟排队的人说：“不好意思，我男朋友帮我找到了正确的插入位置，是在你前面，麻烦你往后退一步，帮我腾个位置出来。”

大家都照着做了，没过多久花花就站在了自己的位置上，她对小胖表示感谢，但是又有些不满意地说：“你是怎么搞的，怎么花了这么长时间？”

小胖诉苦说：“花花你是不知道，排队的人实在太多了，而且来自世界各地，说什么话的人都有，我是使尽了浑身解数才找到这个正确位置的啊！”

“是吗？那你告诉我你是怎么做的？”

“还能怎么做？一个个问过来呗，我还是用Python语言写个函数给你看吧。”

#顺序查找age的插入位置，left和right是非递增列表lst的左右边界def insert_pos(lst,left,right,age): pos = right+1 #花花的初始位置序号 #不断询问前面人的年龄，直到到达队伍前端或遇到不小于花花的人 while pos > left and lst[pos-1] < age: pos -= 1    return pos #返回正确的插入位置

“原来你是用顺序查询的办法啊，怪不得这么慢。前面的队伍都已经是有序的了，难道你就不能动动脑子吗？”

“动动脑子？哦，我想起来了，前面队伍有序，我可以用折半查找法寻找插入位置，这样速度可以快上很多！”

“现在才想到，刚才干什么吃的去了！真是个猪脑袋！罚你用Python语言把折半查找插入位置的函数给我写出来。”

“夫人，遵命！”

#折半查找age的插入位置,left和right是非递增列表lst的左右边界def binary_insert_pos(lst,left,right,age): while left <= right: mid = (left + right) // 2 if age > lst[mid]: #中间值小于age，则插入位置在左半边 right = mid - 1 else: #否则插入位置在右半边 left = mid + 1    return left #返回正确的插入位置

小胖从诚实国回来，刚好赶上公司给大家发奖金，大家在财会室门口挤作一团，领导看不下去了，让小胖帮忙组织大伙把队伍排好。小胖想起来自己在诚实国排队买烧饼的经历，就依葫芦画瓢，很快把队伍排好了。

领导看了非常满意，问小胖怎么做到的。

小胖很谦虚地回答：“其实也很简单，我这是借鉴了诚实国人排队的方法。先随便找一个人排在最前面，然后第二个人跟在他后面，如果第二个人比第一个人大，就插队到前面，否则不动。这样前两个人是有序的。接下来第三个人用同样的方法插队，找到正确的位置，这样前三个人是有序的。采用同样的方法，把后面的人一个个插入，直到队伍全部有序。”

“嗯嗯，不错，你用Python语言把程序写出来吧，我要把这个好办法推广到全公司。”

“领导，遵命！”

#直接插入排序算法def insert_sort(lst): for i in range(1,len(lst)): #从第二个元素开始插入排序 t = lst[i]  j = i  while j > 0 and lst[j-1] < t: #一边比较一边向后退腾出位置 lst[j] = lst[j-1]  j -= 1  lst[j] = t#折半查找插入排序算法def binary_insert_sort(lst): for i in range(1,len(lst)): #从第二个元素开始插入排序 t = lst[i] pos = binary_insert_pos(lst,0,i-1,lst[i]) #调用前面的折半查找插入位置函数 for i in range(i,pos,-1): #元素后移，为t腾出插入位置 lst[i] = lst[i-1]        lst[pos] = t 

几十年过去了，此时的小胖已是排序界的高手，插入排序算法运用得炉火纯青。几十年的排序经验让他认识到插入排序在对“基本有序”的数据操作时，效率非常高，都快赶上线性排序的效率了（所谓“基本有序”是指待排序的数组逆序数比较少）。但进行插入操作时，每次只能将数据移动一位，难免出现大量重复移动。例如在诚实国排队的时候，小孩子就特别受累，每次后面来一个人，他们就要后退一步，所以有些小孩索性直接一次性多退几步，让后来的人直接站到他前面去。

小胖因此得到启发，如果将元素尽可能快的移动到它“该去”的地方，肯定会减少重复移动的次数，提高效率。小胖的想法是把全部元素分组排序，将所有距离为步长gap的元素放在同一个组中，通过“跳跃式移动”的方法，能让元素每次移动一大步，即步长gap>1，大大提高了移动的效率。一趟排序下来，虽然同组的元素没有挨在一起，各组元素相互隔开，但是由于每一组都已经各自排好序了，所以整个序列的“有序性”还是变好了。

我们来看一个例子：

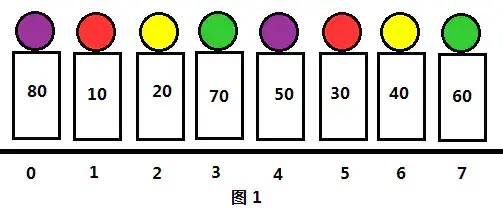
图1是原始序列，序列长度len=8，我们先取步长gap=len/2=4，把序列分成4组（容易看出来，分组数量和步长相等）。地面下方的序号表示每个人所在的位置，用0-7表示；人体身上的数字表示其年龄，人体头部的颜色相同表示他们在同一组，此时分组情况为（0,4），（1,5），（2,6），（3,7）。

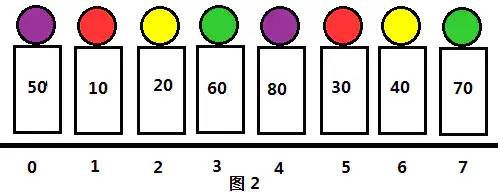
我们对同组的人进行简单插入排序，结果如图2所示。一趟排序下来，虽然同组的元素没有挨在一起，各组元素相互隔开，但是由于每一组都已经各自排好序了，所以整个序列看上去还是比以前要“有序”些，即逆序数要少一些。

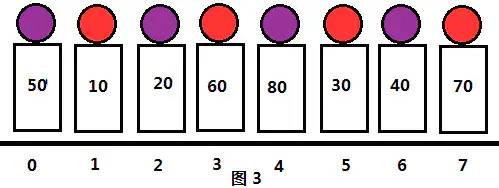
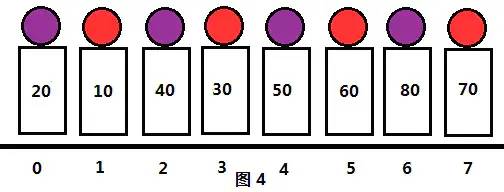
接下来我们取更小的步长gap=2，把序列分成2组，此时分组情况为（0,2，4，6），（1,3，5，7）。各元素位置和分组情况如图3所示：

我们对同组的人进行简单插入排序，结果如图4所示。很明显，现在逆序数又少了很多，整个序列变得更加“有序”了。

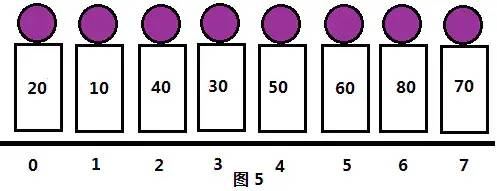
同样的，我们继续减少步长，取gap=1，把序列分成1组，此时各元素位置和分组情况如图5所示：

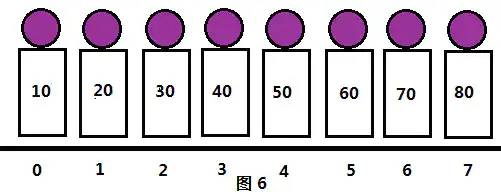
现在步长gap=1，就是普通的插入排序。现在整个序列已经是“基本有序”了，直接插入排序也能高效完成。排序结果如图6所示：

通过上面的例子我们可以看到，将相隔一定步长的元素组成一个子序列，分别对他们进行插入排序，可以实现跳跃式的移动，使得排序的效率提高。经过一轮分组排序后，虽然整个序列还是无序的，但每个相互隔开的子序列已经变得有序，总的逆序数减少，整个序列变得更加“有序”了。每完成一轮分组排序后，我们就将步长减半，继续分组排序，直至步长step=1，就变成普通的插入排序了。由于此时整个序列已经“基本有序”了，直接插入排序也能高效完成。

这种另类的插入排序算法就是传说中的“希尔排序”。用Python语言实现代码如下：

#希尔排序def shell_sort(lst): gap = len(lst) // 2 while gap > 0: for i in range(gap,len(lst)): #将相隔为step的元素组成一个子序列，分别对各组进行插入排序 t = lst[i] j = i while j >= gap and lst[j-gap] > t: #跳跃插入，跳跃距离为gap lst[j] = lst[j-gap] j -= gap lst[j] = t        gap //= 2 #步长gap每次减半

希尔排序的关键在于不能将元素随便分组后各自排序，而是将相隔一定步长的元素组成一个子序列，实现跳跃式的移动，使得排序的效率提高。

步长的选择是希尔排序的重要部分。前面的算法中，我们让步长step每次减半，这是最简单的方法，但不是唯一的方法。事实上只要满足让步长逐渐减小，最终步长为1的规则，无论采用何种递减规律都可以。算法最开始以某个步长进行排序，然后会继续以更小的步长排序，最终算法以步长为1排序。当步长为1时，算法变为插入排序，这就保证了数据一定会被排序。

Donald Shell 最初建议选择步长step=n/2，然后让步长step每次减半，直到步长step=1。虽然这样取可以比O(n^2)类的算法（插入排序）更好，但这样仍然有减少平均时间和最差时间的余地。可能希尔排序最重要的地方在于当用较小步长排序后，以前用的较大步长仍然是有序的。比如，如果一个数列以步长5进行了排序然后再以步长3进行排序，那么该数列不仅是以步长3有序，而且是以步长5有序。如果不是这样，那么算法在迭代过程中会打乱以前的顺序，那就不会以如此短的时间完成排序了。

已知的最好步长序列是由Sedgewick提出的 (1, 5, 19, 41, 109,...)，该序列的项来自 9 * 4^i - 9 * 2^i + 1 和 4^i - 3 * 2^i + 1 这两个算式。这项研究也表明在希尔排序中比较是最主要的操作，而不是交换。用这种步长序列的希尔排序比插入排序和堆排序都要快，甚至在小数组中比快速排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

另一个在大数组中表现优异的步长序列是(斐波那契数列除去0和1将剩余的数以黄金分区比的两倍的幂进行运算得到的数列)：（1, 9, 34,182, 836, 4025, 19001, 90358,428481, 2034035, 9651787, 45806244, 217378076,1031612713, …）。

“Python算法之旅”微信群等着你

扫码加入“Python算法之旅”微信群，和斌哥面对面交流，更多资料和更有趣的话题等你一起来分享。