第七章 内排序——插入排序
Posted 凯哥的故事
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第七章 内排序——插入排序相关的知识,希望对你有一定的参考价值。
插入排序
本节将介绍两种插人排序方法:直接插入排序和希尔排序。
直接插入排序
直接插入排序(Straight Insertion Sort)是一种简单的排序方法,其基本思想是每趟将一条待排序的记录,按其关键字值的大小插入到前面已经排好序的记录序列中的适当位置,直到全部记录插入完成为止。
假设排序表中有n个记录,存放在数组r中,重新排列记录的存放顺序,使得它们按照关键字值从小到大有序,即r[0].key ≤ r[1].key ≤…≤ r[n-1].key。
首先来看看将一条记录插入到有序表中的方法:
已知一组待排序的记录的关键字序列为{52,39,67,95,79,8,25,52'},直接插入排序过程如下图所示。

直接插入排序算法的基本要求是,假设待排序的记录存放在数组r[0..n-1]中。开始时,先将第0个记录组成一个有序的子表,然后依次将后面的记录插入到这个子表中,并且一直保持子表的有序性。
直接插入排序算法的主要步骤归纳如下:

不带监视哨的直接插入排序算法。
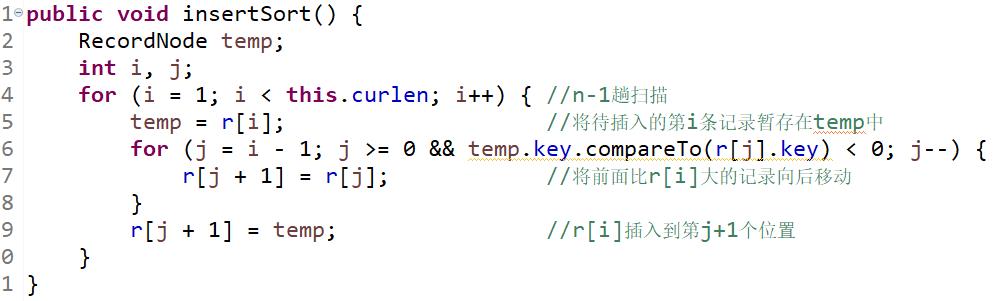
左右滑动或点击查看全图
此算法中第6行的循环条件“j>=0 &&temp.key.compareTo(r[j].key)<0”中“j>=0”用来控制下标越界。为了提高算法效率,可对该算法进行如下改进:首先将待排序的n条记录从下标为1的存储单元开始依次存放在数组r中,再将顺序表的第0个存储单元设置为一个“监视哨”,即在查找之前把r[i]赋给r[0],这样每循环一次只需要进行记录的比较,不需要比较下标是否越界,当比较到第0个位置时,由于“r[0].key==r[i].key”必然成立,将自动退出循环,所以只需设置一个循环条件:“temp.key.compareTo(r[j].key)<0”。
改进后的算法描述如下:

需要说明的是,对于具有n个存储单元的顺序表,在该算法中因为r[0]用于存放监视哨,正常的记录只能存放在下标从1到n-1的存储单元中,即具有n个存储单元的顺序表只能存放n-1个记录。
算法性能分析:
(1)空间复杂度。仅用了一个辅助单元r[0],空间复杂度为O(1)。
(2)时间复杂度。从时间性能上看,有序表中逐个插入记录的操作进行了n-1趟,每趟排序的操作分为比较关键字和移动记录,而比较的次数和移动记录的次数取决于待排序列关键字的初始排列状况。最好情况是当待排序记录序列已按关键字值有序时,每趟排序只需与记录关键字进行1次比较,2次移动。总的比较次数达到最小值,即n-1次,总的移动次数也达到最小值,即2(n-1)次;最坏情况是当待排序记录序列已按关键字值逆序时,每趟排序都要将待插入的记录插入到记录表的最前面位置,为此,第i趟直接插入排序需要进行关键字比较的次数为i次,移动记录的次数为i+2次,总的比较次数为n(n-1)/2;总的移动次数为n(n-1)/2+2n。
当待排序记录是随机序列的情况下,即待排序记录出现的概率相同,则第i趟排序所需要的比较和移动次数可取上述最小值与最大值的平均值,约为i/2,总的平均比较和移动次数均约为n²/4,因此,直接插入排序的时间复杂度为O(n²)。
(3)算法稳定性。直接插入排序是一种稳定的排序算法。
希尔排序
直接插入排序算法简单,在n值较小时,效率比较高;当n值很大时,若待排序列是按关键字值基本有序,效率依然较高,其时间效率可提高到O(n)。希尔排序正是从这两点出发给出的插入排序的改进方法。
希尔排序(Shell Sort),又称缩小增量排序,该算法是由D.L.Shell在1959年首先提出来的。希尔排序的基本思路是:先选取一个小于n的整数di(称为增量),然后把排序表中的n个记录分为di个子表,从下标为0的记录开始,间隔为di的记录组成一个子表,在各个子表内进行直接插入排序。在一趟之后,间隔为di的记录组成的子表已有序,随着有序性的改善,逐步减小增量di,重复进行上述操作,直到di=1,使得间隔为1的记录有序,也就是整个序列都达到有序。
例如,设排序表关键字序列(52,39,67,95,70,8,25,52',56,5),增量分别取5、3、1,则希尔排序过程如下图所示。
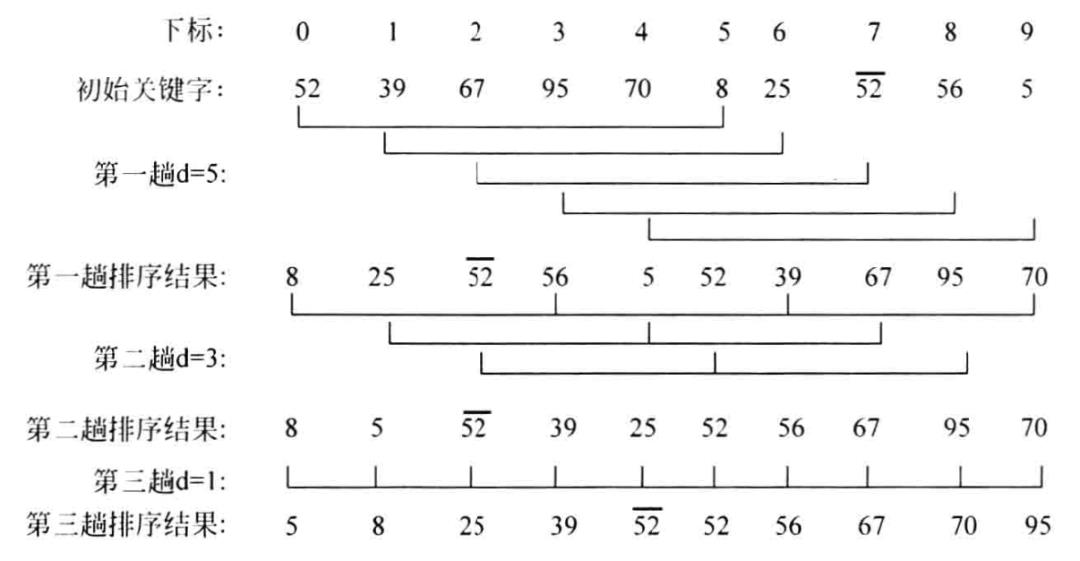
希尔排序算法的主要步骤归纳如下:

希尔排序算法。
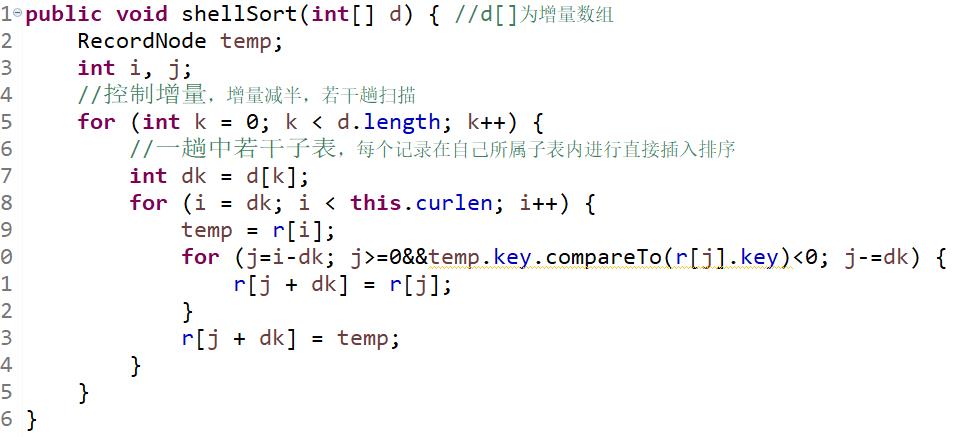
左右滑动或点击查看全图
算法性能分析:
(1)空间复杂度。由于希尔排序中用到了直接插入排序,而直接插入排序的空间复杂度为O(1),因此,希尔排序的空间复杂度也为O(1)。
(2)时间复杂度。希尔排序的时间效率分析很困难,关键字的比较次数与记录的移动次数依赖于增量序列的选取,在特定情况下可以准确估算出关键字的比较次数和记录的移
动次数。目前还没有一种选取最好的增量序列的方法,但目前经过大量研究,已得出一些局部结论。例如:

(3)算法稳定性。从上图的排序结果可以看出,希尔排序是一种不稳定的排序算法。

以上是关于第七章 内排序——插入排序的主要内容,如果未能解决你的问题,请参考以下文章