OpenCV轮廓层次分析实现欧拉数计算

Posted 2021-04-25 OpenCV学堂

欧拉数定义

二值图像分析中欧拉数重要的拓扑特征之一，在图像分析与几何对象识别中有着十分重要的作用，二值图像的欧拉数计算公式表示如下：
E = N – H 其中 
E表示计算得到欧拉数
N表示联通组件的数目
H表示在联通组件内部的洞的数目
下图是二值图像，白色背景，两个对象、分析计算得到欧拉数的例子：

可以看到通过简单的欧拉数属性就可以对它们进行区分。左侧对象中有两个联通区域，所以N=2，没有洞孔区域，所以H=0， 计算得到欧拉数目为 2 – 0 = 。右侧是大写字母B，它只有一个联通区域所以N = 1， 内部有两个洞孔区域所以H = 2，最终计算得到欧拉数为 2 – 1 = -1。对于任意一个几何形状来说，如果我们要求得它的欧拉数，就首先要分析它的轮廓结构，然后根据轮廓层次结构计算得到N与H值。

欧拉数是图像几何识别中重要的属性，举例如下图中三个英文字母

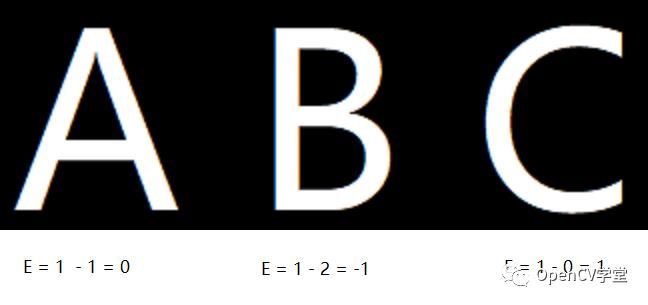 对字母A来说它的内部有一个黑色孔洞，所以它的H=1，其本身是一个联通组件所以N =1，最终计算得到欧拉数为 E = 1 -1 = 0，同样可以计算B与C它们的欧拉数分布为-1与1，可见通过欧拉数属性可以轻而易举的区分ABC三个英文字母。

二：轮廓层次信息获取

在OpenCV对二值图像进行轮廓分析输出的层次结构会保存在一个Vec4i的结构体中，这里有必要首先看一下轮廓发现API及其相关参数的解释：

void cv::findContours(
InputOutputArray image,
OutputArrayOfArrays contours,
OutputArray hierarchy,
int mode,
int method,
Point offset = Point() 
)
image参数表示输入的二值图像
contours表示所有的轮廓信息，每个轮廓是一系列的点集合
hierarchy表示对应的每个轮廓的层次信息，我们就是要用它实现对最大轮廓欧拉数的分析
mode表示寻找轮廓拓扑的方法，如果要寻找完整的层次信息，要选择参数RETR_TREE
method表示轮廓的编码方式，一般选择简单链式编码，参数CHAIN_APPROX_SIMPLE
offset表示是否有位移，一般默认是0

上面的参数中最重要的是hierarchy信息，它的输出是vector<Vec4i> 每个轮廓对应的Vec4i结构体里面四个值解释如下：

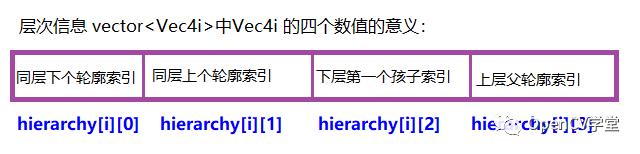
上面的索引如果是负数就表示没有相关层次信息，如果是非负数就表示有相关的层次关系信息。此外轮廓发现函数对输入image图像的要求必须满足

• 背景是黑色 ，0表示

• 对象或者前景是白色，1表示

三：欧拉数计算方法

有了轮廓的层次信息与每个轮廓的信息之后，尝试遍历每个轮廓，首先通过调用findContours就可以获取二值图像的轮廓层次信息，然后遍历每个轮廓，进行层次遍历，获得每层子轮廓的总数，最终根据轮廓层级不同分为孔洞与连接轮廓的计数，二者想减得到每个独立外层轮廓的欧拉数。

二值化与轮廓发现的代码如下：

Mat gray, binary;
cvtColor(src, gray, COLOR_BGR2GRAY);
threshold(gray, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);
vector<Vec4i> hireachy;
vector<vector<Point>> contours;
findContours(binary, contours, hireachy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point());

获取同层轮廓的代码如下：

vector<int> current_layer_holes(vector<Vec4i> layers, int index) {
    int next = layers[index][0];
    vector<int> indexes;
    indexes.push_back(index);
    while (next >= 0) {
        indexes.push_back(next);
        next = layers[next][0];
    }
    return indexes;
}

使用队列迭代寻找遍历每层的代码如下：

while (!nodes.empty()) {
    // 当前层总数目
    if (index % 2 == 0) { // 联通组件对象
        n_total += nodes.size();
    }
    else { // 孔洞对象
        h_total += nodes.size();
    }
    index++;
    // 计算下一层所有孩子节点
    int curr_ndoes = nodes.size();
    for (int n = 0; n < curr_ndoes; n++) {
        int value = nodes.front();
        nodes.pop();
        // 获取下一层节点第一个孩子
        int child = hireachy[value][2];
        if (child >= 0) {
            nodes.push(child);
        }
    }
}

四：运行与测试结果

测试图一（ABC）与运行结果：

测试图二与运行结果

五：完整源代码

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

vector<int> current_layer_holes(vector<Vec4i> layers, int index);

int main(int argc, char** argv) {
    Mat src = imread("D:/holes.png");
    if (src.empty()) {
        printf("could not load image...\n");
        return -1;
    }
    namedWindow("input", CV_WINDOW_AUTOSIZE);
    imshow("input", src);

    Mat gray, binary;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    threshold(gray, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);

    vector<Vec4i> hireachy;
    vector<vector<Point>> contours;
    findContours(binary, contours, hireachy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point());
    Mat result = Mat::zeros(src.size(), src.type());
    for (size_t t = 0; t < contours.size(); t++) {
        int next = hireachy[t][0]; // next at the same hierarchical level
        int prev = hireachy[t][1]; // prev at the same hierarchical level
        int child = hireachy[t][2]; // first child
        int parent = hireachy[t][3]; // parent
        printf("next %d, previous %d, children : %d, parent : %d\n", next, prev, child, parent);
        drawContours(result, contours, t, Scalar(0, 255, 0), 2, 8);
        // start calculate euler number
        int h_total = 0;
        int n_total = 1;
        int index = 1;
        vector<int> all_children;
        if (child >= 0 && parent < 0) {
            // 计算当前层
            queue<int> nodes;
            vector<int> indexes = current_layer_holes(hireachy, child);
            for (int i = 0; i < indexes.size(); i++) {
                nodes.push(indexes[i]);
            }
            while (!nodes.empty()) {
                // 当前层总数目
                if (index % 2 == 0) { // 联通组件对象
                    n_total += nodes.size();
                }
                else { // 孔洞对象
                    h_total += nodes.size();
                }
                index++;
                // 计算下一层所有孩子节点
                int curr_ndoes = nodes.size();
                for (int n = 0; n < curr_ndoes; n++) {
                    int value = nodes.front();
                    nodes.pop();
                    // 获取下一层节点第一个孩子
                    int child = hireachy[value][2];
                    if (child >= 0) {
                        nodes.push(child);
                    }
                }
            }
            printf("hole number : %d\n", h_total);
            printf("connection number : %d\n", n_total);
            // 计算欧拉数
            int euler_num = n_total - h_total;
            printf("number of euler : %d \n", euler_num);
            drawContours(result, contours, t, Scalar(0, 0, 255), 2, 8);
            // 显示欧拉数
            Rect rect = boundingRect(contours[t]);
            putText(result, format("euler: %d", euler_num), rect.tl(), FONT_HERSHEY_SIMPLEX, 1.0, Scalar(255, 255, 0), 2, 8);
        }
        if (child < 0 && parent < 0) {
            printf("hole number : %d\n", h_total);
            printf("connection number : %d\n", n_total);
            int euler_num = n_total - h_total;
            printf("number of euler : %d \n", euler_num);
            drawContours(result, contours, t, Scalar(255, 0, 0), 2, 8);
            Rect rect = boundingRect(contours[t]);
            putText(result, format("euler: %d", euler_num), rect.tl(), FONT_HERSHEY_SIMPLEX, 1.0, Scalar(255, 255, 0), 2, 8);
        }

    }

    imshow("result", result);
    waitKey(0);
    return 0;
}

vector<int> current_layer_holes(vector<Vec4i> layers, int index) {
    int next = layers[index][0];
    vector<int> indexes;
    indexes.push_back(index);
    while (next >= 0) {
        indexes.push_back(next);
        next = layers[next][0];
    }
    return indexes;
}

PS:代码未经更多严格测试，仅供参考！

【推荐阅读】

学易而好难 行易而力难 耻易而知难

关注【OpenCV学堂】

长按或者扫码二维码即可关注