贪心算法（14）：水箱连接问题

Posted 2021-04-25 中学生编程与信息学竞赛自学

本课程是从少年编程网转载的课程，目标是向中学生详细介绍计算机比赛涉及的编程语言，数据结构和算法。编程学习最好使用计算机，请登陆 www.3dian14.org (免费注册，免费学习)。

某居住地中的有一些房屋，现在要为房屋安装水箱解决供水问题，也就是水的来源是安装在屋顶的水箱。由于有些房屋之间已经有供水管道相连，为节约成本，有水箱的房屋A可以通过出水管向与它连的房屋B供水，方法是把房屋A的出水管通过A与B之间的管道与房屋B的进水管相连，这样房屋B可以从A相连的水管中获得水，自己就不需要安装水箱了。同样，房屋B也可以进一步通过出水管继续向与B相连的房屋C供水，只要把房屋B的出水管与房屋C的进水管相连即可。

这样就形成一条供水路径A->B->C->.....->W。作为起点的房屋A没有进水管，需要安装水箱，作为水源。路径上的其他房屋，通过管道相连取水，无需再安装水箱，而处于路径上最后一站的房屋W，需要为它安装一个水龙头，作为该条供水路径的结束。

为使问题简单化，假设每个房屋最多只能安装一根进水管以及一根出水管。这样对于整片居住地来说，可能会形成多条供水路径，每条路径只有一个水箱和一个水龙头，它们成对出现，作为路径的始终。需要的水箱和水龙头对数越少，表明建设成本越低、效率越高。

现在假设整数n和p分别表示房屋数量和管道数量，而房屋之间现有的连接管道包含三个输入值：a_i，b_i，d_i，它们表示从房屋a_i到房屋b_i的直径为d_i的管道，请找出建立供水网络连接的高效解决方案：也就是找出把房屋通过管道相连的路径以及需要安装水箱的房屋（路径起点）、需要安装水龙头的房屋（路径终点）以及沿途路径中管道的最小直径。

输入包含安装在第一行的水箱和水龙头对的数量，接下来的t行包含三个整数：水箱的房屋门牌号，水龙头的房屋门牌号和它们之间的管道的最小直径。

下面是一个例子。

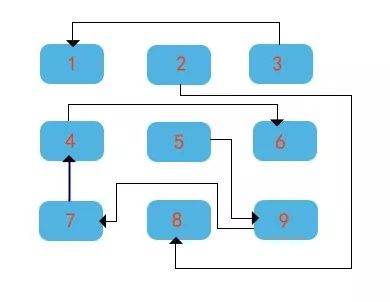
输入 :9 6
       7 4 98
       5 9 72
       4 6 10
       2 8 22
       9 7 17
       3 1 66
输出 :3
        2 8 22
        3 1 66
        5 6 10

三条通路：

通路1：3->1

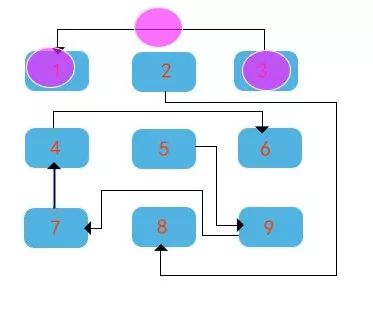
通路2：5->9->7->4->6

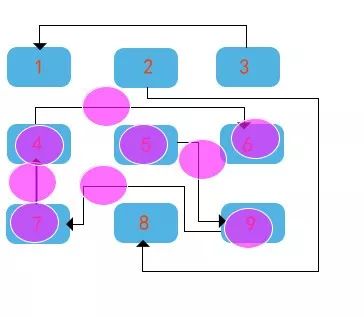
通路3：2->8

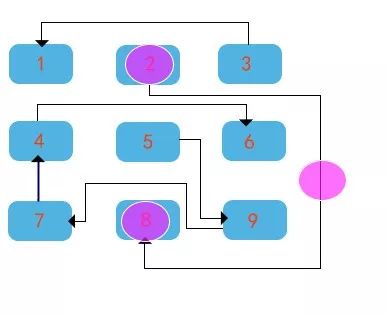
思路分析

我们采用深度优先算法（Depth-First-Search，简称DFS）。从某个房屋开始，采用DFS来找出所有不同的水管路径连接方案，可以找到的不同路径的条数就是我们的答案。

因为水箱只能安装在有输出管道的房屋上，并且该房屋没有输入管道，所以我们就先找到符合上述条件的房屋，然后从它们开始，进行DFS搜索。也就是从还没有检查过的没有输入管道只有输出管道的房屋进行DFS搜索。

 算法描述

算法描述如下：

１）找一个没有输入管道的房屋：

　　如果找到符合条件的房屋H，并且它还没有被访问过，那么它是一条供水路径的起点，需要安装水箱；转步骤２）

　　如果没有找到符合条件的房屋，那么算法结束

2）从该房屋开始进行DFS搜索，规则如下：

     如果有从该房屋开始的管道，它与房屋H' 相连，那么把H'加入路径，供水路径从H->H’，返回第二步继续房屋H'进行DFS搜索。

     如果没有从该房屋开始的管道，那么它就是路径的最后一个房屋，需要安装水龙头，返回第一步

代码的实现

上述算法C++实现代码如下，为简化编程，用了C++的STL。

// C++ 代码

#include <bits/stdc++.h> 

using namespace std; 

  

// n,p分别是房屋以及水管的数目

int n, p; 

  

//数组rd中保存了水管的终点房屋号

//我们这里假设最大的水管数为1000

int rd[1000]; 

//数组rd中保存了水管的起点房屋号

int cd[1000]; 

//保存水管的直径

int wt[1000]; 

  

//为简单，用向量保存结果

//向量a保存通路的起点，

//向量b保存对应通路的终点

//向量c保存对应通路的最小直径

vector<int> a; 

vector<int> b; 

vector<int> c; 

  

int ans; 

 

//用于找出最小管径

int dfs(int w) 

{ 

    if (cd[w] == 0) 

        return w; 

    if (wt[w] < ans) 

        ans = wt[w]; 

    return dfs(cd[w]); 

} 

  

void solve(int arr[][3]) 

{ 

    int i = 0; 

  

    while (i < p) { 

          

        int q = arr[i][0], h = arr[i][1], 

            t = arr[i][2]; 

          

        cd[q] = h; 

        wt[q] = t; 

        rd[h] = q; 

        i++; 

    } 

      

    a.clear(); 

    b.clear(); 

    c.clear(); 

      

    for (int j = 1; j <= n; ++j) 

      

       //如果一个管道没有终点，只有起点，

       //那么我们可以从该管道起点开始进行找出DFS路径

        if (rd[j] == 0 && cd[j]) { 

            ans = 1000000000; 

            int w = dfs(j); 

              

            // We put the details of component 

            // in final output array 

//保存通路的节点信息到输出向量中

            a.push_back(j); 

            b.push_back(w); 

            c.push_back(ans); 

        } 

          

    cout << a.size() << endl; 

    for (int j = 0; j < a.size(); ++j) 

        cout << a[j] << " " << b[j]  

             << " " << c[j] << endl; 

} 

  

//主程序

int main() 

{ 

    n = 9, p = 6; 

  

    memset(rd, 0, sizeof(rd)); 

    memset(cd, 0, sizeof(cd)); 

    memset(wt, 0, sizeof(wt)); 

  

    int arr[][3] = { { 7, 4, 98 }, 

                    { 5, 9, 72 }, 

                    { 4, 6, 10 }, 

                    { 2, 8, 22 }, 

                    { 9, 7, 17 }, 

                    { 3, 1, 66 } }; 

  

    solve(arr); 

    return 0; 

} 

请点击阅读原文来观看动画交互课件。