贪心算法：警察与小偷问题

Posted 2021-04-25 中学生编程与信息学竞赛自学

本课程是从少年编程网转载的课程，目标是向中学生详细介绍计构和算法。编程学习最好使用计算机，请登陆 www.3dian14.org (免费注册，免费学习)。

本课继续讲解贪心算法相关的习题：警察抓小偷的经典问题。

假设小偷与警察依次排列成一个队列，规定每名警察只能抓捕一个小偷，而且他能抓捕的小偷与他相邻的距离不能超过k个位置，请找出所有警察能抓到的最多小偷数目。

我们用数组来表示警察和小偷的排成的队列：给定大小为n的数组，其具有以下约束条件：

• 数组中的每个元素要么是警察（用字母'P'表示）要么是小偷（用字母'T'表示)；

• 每名警察只能抓一个小偷；

• 一名警察只能抓捕离自己所在位置距离在k以内的小偷，也就是警察只能抓捕与他的数组下标相差小于或等于k的小偷。

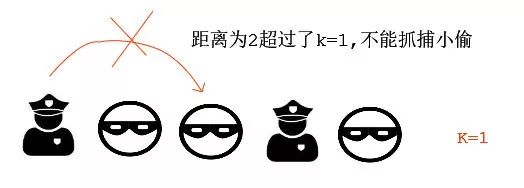
下面我们看几个例子：

【例题1】

输入 : arr[] = {'P', 'T', 'T', 'P', 'T'},  k = 1.

输出 : 2（警察最多能抓到2个小偷）

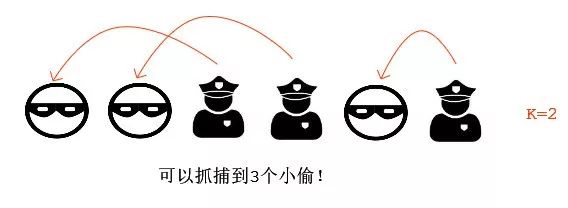
【例题2】

输入 : arr[] = {'P', 'T', 'T', 'P', 'T'},  k = 1.

输出 : 3（警察最多能抓到3个小偷）

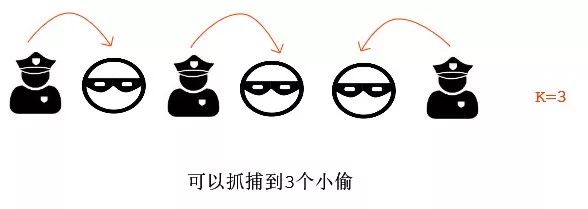
【例题3】

输入 :arr[] = {'P', 'T', 'P', 'T', 'T', 'P'},   k = 3.

输出 : 3（警察最多能抓到3个小偷）

在继续讲解算法之前，请你先考虑一下如何解决上述问题？

思路分析

简单粗暴的方法就是暴力搜索和检查所有可能的警察和小偷的组合，并返回其中包含最多小偷的组合。

但是这种暴力搜索方法具有指数级的时间复杂度，所以我们要另想他法，提高搜索效率。

一种有效的解决方案就是使用贪心算法。但是应该针对哪个特性来运用贪心算法呢？

我们可以尝试使用下列贪心策略："从左开始，每个警察都抓住离他最近的小偷。”

我们来运用该策略来看看例子3，输出3，结果是正确的。

我们来运用该策略来看看例子2，输出2，结果是错误的。

那么我们再来修改一下贪心策略："从左开始，每个警察都抓住离他最远的小偷。”

我们来运用该策略来看看例子2，输出3，结果是正确的。

我们来运用该策略来看看例子3，输出2，结果是错误的。

或者我们尝试一下从右边开始，每个警察都抓住离他最近（或最远）的小偷？

你会发现这两个策略也不对。

那该怎么办呢？

 算法描述

我们换个角度，从左到右，把警察和小偷依序配对。设置两个标尺 p和 t，它们分别指向当前待分析的警察和小偷的位置：

1. 如果p指向的警察可以抓捕到t指向的小偷（p和t的值相差在k以内），那么就把他们配对（输出）。然后，依次把标尺p和t向右移动，分别指向找到的下一个警察和下一个小偷。

2. 如果由于距离太远，导致p指向的警察不能抓捕到t指向的小偷，那么我们从p和t中选择较小的标尺（假设是p比较小)，然后向右移动，让p指向下一个警察。同样，如果t比较小，那么将t向右移动，指向下一个小偷。

3. 重复1）和2），直到标尺p和t都指向了最右的警察和小偷位置。

下面的动图描述了例子2的解题过程。

在上述算法中，p和t依次从数组的左端移动到数组的右端，因此该算法的时间复杂度是O(N)，N是数组中的元素个数。

代码实现

下面是一种C++的代码实现，其中使用了标准模板库来简化实现方式。

#include <iostream> 

#include <vector> 

#include <cmath> 

  

using namespace std; 

  

// 返回能抓到的最多的小偷数目

int policeThief(char arr[], int n, int k) 

{ 

    int res = 0; 

    vector<int> thi; 

    vector<int> pol; 

  

    //把警察和小偷的对应的元素下标依次放入向量pol和thi中 

    for (int i = 0; i < n; i++) { 

        if (arr[i] == 'P') 

            pol.push_back(i); 

        else if (arr[i] == 'T') 

            thi.push_back(i); 

    }    

  

   //P 和 T分别指向当前正在处理的警察和小偷

    int P = 0, T = 0; 

    while (T < thi.size() && P < pol.size()) { 

  

        // 够得着，警察可以抓住小偷 

        if (abs(thi[T] - pol[P]) <= k) { 

            res++; 

            T++; 

            P++; 

        } 

  

        // 够不着，将P或T中较小的指向下一个警察或小偷

        else if (thi[T] < pol[P]) 

            T++; 

        else

            P++; 

    } 

  

    return res; 

} 

int main() 

{ 

    int k, n; 

  

    char arr1[] = { 'P', 'T', 'T', 'P', 'T' }; 

    k = 2; 

    n = sizeof(arr1) / sizeof(arr1[0]); 

    cout << "能抓住的最多小偷数: "

         << policeThief(arr1, n, k) << endl; 

  

    char arr2[] = { 'T', 'T', 'P', 'P', 'T', 'P' }; 

    k = 2; 

    n = sizeof(arr2) / sizeof(arr2[0]); 

    cout << "能抓住的最多小偷数: "

         << policeThief(arr2, n, k) << endl; 

  

    char arr3[] = { 'P', 'T', 'P', 'T', 'T', 'P' }; 

    k = 3; 

    n = sizeof(arr3) / sizeof(arr3[0]); 

    cout << "能抓住的最多小偷数: "

         << policeThief(arr3, n, k) << endl; 

  

    return 0; 

} 

请点击阅读原文来观看动画交互课件。