贪心算法(13):书架问题
Posted 中学生编程与信息学竞赛自学
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贪心算法(13):书架问题相关的知识,希望对你有一定的参考价值。
本课程是从少年编程网转载的课程,目标是向中学生详细介绍计构和算法。编程学习最好使用计算机,请登陆 www.3dian14.org (免费注册,免费学习)。
本课继续讲解贪心算法的习题:书架问题。
有一个书房。现在要订购一批书架,这些书架背靠书房的某一面墙安放。假设该墙壁的长度为w,而书架有两种类型,它们的长度分别为m和n。
请确定需要订购的每种类型书架的数量,使得它们靠墙安放后,空出墙壁的长度最小。并且注意,由于较长的书架比较便宜,所以首选较长的书架。不过成本是次要因素,首要任务还是尽量减少墙壁的空余长度。
【例题1】
输入 : 墙壁长度 w = 24 而两种书架的长度分别是 m = 3 n = 5
输出 : 订购这两种类型的书架数量分别为3和3。
也就是每种书架的数量都为3个。这样书架排列起来的总长度
3*m + 3*n = 3*3 + 3*5 = 24 = w
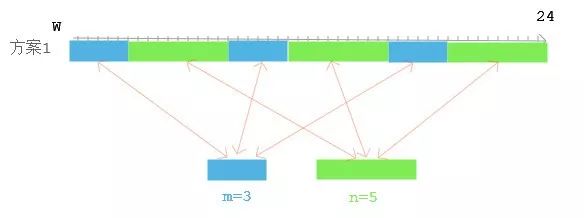
正好排满墙壁,不留任何空余空间,因此剩余空间是0
另外一种方案是长度为m的书架为8而长度为n的书架为0个,也就是书架排列的总长度是
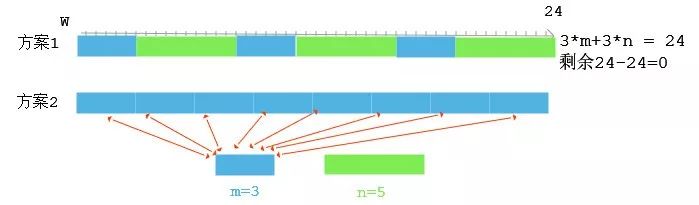
8*m + 0*n = 24 + 0 = 25 = w
也正好排满墙壁,剩余空间也是0。但是第一种方案用了3个长度为5的大书架,而第二种方案没有用到长度为5的书架,所以第一种方案比较便宜,正确答案是第一种方案。
【例题2】
输入 : 墙壁长度 w = 29 而两种书架的长度分别是 m = 3 n = 9
输出 : 订购这两种类型的书架数量分别为多少?
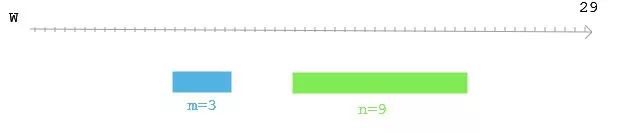
思考:如何解决这个问题?如果你看了之前的贪心算法的课件,应该不难吧?

算法描述
一种简单而有效的方法是尝试适合墙壁长度的所有可能的书架组合。同时为了节省成本,我们要优先使用大的书架。
算法如下:
从0 开始,先逐个增加大书架的数目,直到再无法放置大书架或者大书架用完为止
对于选定的每种大书架的数目,计算剩余空间以及剩余空间最多能安放的小书架数目
对于上述选定的每种大书架和小书架的组合,我们计算它的空余空间
从上述所有组合种选出空余空间最少的组合,若空余空间相同,则优先选用大书架更多的组合方案
代码的实现
上述算法C++实现代码如下,为简化编程,用了C++的STL。
// C++程序实现书架放置问题
#include<bits/stdc++.h>
using namespace std;
void minSpacePreferLarge(int wall, int m, int n)
{
// 初始化输出方案的变量,
//注意num_m为较短长度的书架数目
//num_n为较长长度的书架数目
//min_empty对应该输出方案的剩余空间
int num_m = 0, num_n = 0, min_empty = wall;
// p和q分别是长度为m的书架和长度为n的书架的个数
// rem是墙壁的空余长度
int p = 0, q = 0, rem;
while (wall >= n)
{
//增加一个长度为 n的书架
q += 1;
wall = wall - n;
// 在剩余墙壁空间上尽可能放置最多的长度为m的书架
p = wall / m;
rem = wall % m;
// 如果当前的方案比之前保留方案的剩余空间更小,则
// 把输出方案更新为当前方案
if (rem <= min_empty)
{
num_m = p;
num_n = q;
min_empty = rem;
}
}
//输出结果,依次为较短的书架个数、较长的书架个数
//以及最后墙壁剩余的空间
cout << num_m << " " << num_n << " "
<< min_empty << endl;
}
// Driver code
int main()
{
int wall = 24, m = 3, n = 5;
if (m<n)
minSpacePreferLarge(wall, m, n);
else
minSpacePreferLarge(wall, n, m);
return 0;
}
下面的动图描述了应用上述算法解决【例题2】的过程。
请点击阅读原文来观看动画交互课件。
以上是关于贪心算法(13):书架问题的主要内容,如果未能解决你的问题,请参考以下文章