贪心算法：活动选择问题

Posted 2021-04-25 中学生编程与信息学竞赛自学

本课程是从少年编程网转载的课程，目标是向中学生详细介绍计算机比赛涉及的编程语言，数据结构和算法。编程学习最好使用计算机，请登陆 www.3dian14.org (免费注册，免费学习)。

我们继续回到上一堂课留下的课外习题：活动选择问题。活动选择问题是很常见的场景。例如各个部门共享一个会议室，利用该算法能使会议室安排尽量多的会议。

【问题】给你n个活动的开始时间和结束时间，从中选择你可以参与的活动，但是同一时间你只能参与一个活动，请找出你可以参与的最多活动数。

例如：考虑下面3个活动a1,a2和a3, 它们{开始时间点,结束时间点}分别为：

a1 {start=10,finish=20}

a2 {start=12,finish=25}

a3 {start=20,finish=30}

贪心算法直接在每一步选择当前看来最好的选择。在开始时，选择活动结束时间最早的那个活动，这样能够给其他活动尽可能的腾出多余的时间。而后每一步都在剩下的活动中选取，也遵循类似的原则。由于获取已经按照结束时间排序好，所以这里第一个选择的活动就是a0，由于a0于时间20结束，马上再找一个活动，只有a2可以选择，a2结束之后再也没有活动可选了。因此得到答案：最多可以参加两个活动（a0,a2）。

算法分析和设计

现在请你设计一种贪心算法解决类似活动选择问题。

我们设计下列贪心算法的贪心策略：选择其余活动中完成时间最短的下一个活动，并且开始时间大于或等于先前所选活动的结束时间。 我们可以根据他们的完成时间对活动进行排序，以便我们始终将下一个活动视为最小完成时间活动。

算法描述如下

1）根据完成时间对活动进行排序

2）从排序的数组中选择第一个活动并输出

3）对已排序数组中的剩余活动执行以下操作：

     如果此活动的开始时间大于或等于先前所选活动的结束时间，则选择此活动并输出；

回到上堂课的习题：考虑下面6个活动，请找出你可以参与的最多活动数

 {start=0,finish=6}

 {start=1,finish=2}

 {start=3,finish=4}

 {start=5,finish=7}

 {start=5,finish=9}

 {start=8,finish=9}

首先按结束时间对它们进行排序：

a0{start=1,finish=2}

a1{start=3,finish=4}

a2{start=0,finish=6}

a3{start=5,finish=7}

a4{start=8,finish=9}

a5{start=5,finish=9}

然后按2)和3)两个步骤进行活动选择。选择过程如下图所示：

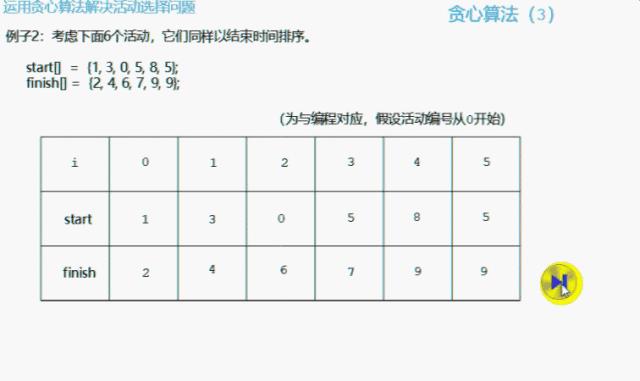
此这种情形下，一个人最多只能参与4个活动：分别是从1开始、3开始、5开始以及8开始的4个活动。你答对了吗？

算法的正确性证明

让给定的一组活动为S = {1,2,3，.. n}，并且已按活动结束时间对所有活动进行排序。 贪心策略总是选择【活动1】。为什么【活动1】始终是最佳解决方案之一？ 

假设存在除了【活动1】以外的另一个最佳解决方案S，并且S选择的第一个活动是【活动k】，而不是【活动1】。现在我们来说明，把【活动k】替换成【活动1】，得到的新方案S‘，{B-{k}}U{1}，必定仍然是一个最佳解决方案，说明如下：因为S 中的活动是独立的，而在排序队列中，【活动1】在所有活动中具有最小的结束时间，因为k不等于1，【活动k】的完成时间必定是大于等与【活动1】的完成时间，因此把【活动k】换成【活动1】后的新方案S‘必定也是最佳解决方案。

算法实现

在以下C/C++代码实现中，假设活动已根据其完成时间进行了排序。

#include<stdio.h> 

//  n   -->  活动个数

//  s[] -->  数组保存所有活动的开始时间 

//  f[] -->  数组保存所有活动的结束时间 

void printMaxActivities(int s[], int f[], int n) 

{ 

    int i, j; 

  

    printf ("选择以下的活动\n"); 

  

    // 第一个活动总是选中 

    i = 0; 

    printf("%d ", i); 

  

    // 依次检查余下的活动

    for (j = 1; j < n; j++) 

    { 

     //如果某活动在之前选择的活动结束之后开始

      if (s[j] >= f[i]) 

      { 

          printf ("%d ", j); 

          i = j; 

      } 

    } 

} 

  

//主程序

int main() 

{ 

    int s[] =  {1, 3, 0, 5, 8, 5}; 

    int f[] =  {2, 4, 6, 7, 9, 9}; 

    int n = sizeof(s)/sizeof(s[0]); 

    printMaxActivities(s, f, n); 

    return 0; 

} 

注意：若是finish数组没有排序，需要先对它进行排序。作为课外练习，请你在上述代码基础上加上排序部分，完成对finish数组的排序。