一份贪心算法区间调度问题解法攻略,拿走不谢
Posted AI科技大本营
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一份贪心算法区间调度问题解法攻略,拿走不谢相关的知识,希望对你有一定的参考价值。
【导读】什么是贪心算法呢?贪心算法可以认为是动态规划算法的一个特例,相比动态规划,使用贪心算法需要满足更多的条件(贪心选择性质),但是效率比动态规划要高。
比如说一个算法问题使用暴力解法需要指数级时间,如果能使用动态规划消除重叠子问题,就可以降到多项式级别的时间,如果满足贪心选择性质,那么可以进一步降低时间复杂度,达到线性级别的。
什么是贪心选择性质呢,简单说就是:每一步都做出一个局部最优的选择,最终的结果就是全局最优。注意哦,这是一种特殊性质,其实只有一小部分问题拥有这个性质。
比如你面前放着 100 张人民币,你只能拿十张,怎么才能拿最多的面额?显然每次选择剩下钞票中面值最大的一张,最后你的选择一定是最优的。
然而,大部分问题都明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文 。
一、问题概述
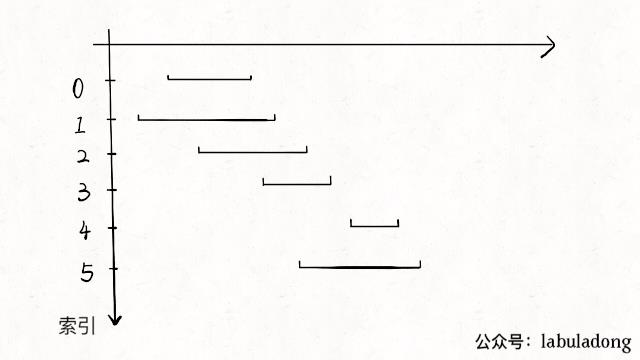
言归正传,本文解决一个很经典的贪心算法问题 Interval Scheduling(区间调度问题)。给你很多形如[start,end]的闭区间,请你设计一个算法,算出这些区间中最多有几个互不相交的区间。
int intervalScheduling(int[][] ints) {}
举个例子,intvs=[[1,3],[2,4],[3,6]],这些区间最多有两个区间互不相交,即[[1,3],[3,6]],你的算法应该返回 2。注意边界相同并不算相交。
这个问题在生活中的应用广泛,比如你今天有好几个活动,每个活动都可以用区间[start,end]表示开始和结束的时间,请问你今天最多能参加几个活动呢?
二、贪心解法
这个问题有许多看起来不错的解决思路,实际上都不能得到正确答案。比如说:
也许我们可以每次选择可选区间中开始最早的那个?但是可能存在某些区间开始很早,但是很长,使得我们错误地错过了一些短的区间。
或者我们每次选择可选区间中最短的那个?或者选择出现冲突最少的那个区间?这些方案都能很容易举出反例,不是正确的方案。
正确的思路其实很简单,可以分为以下三步:
-
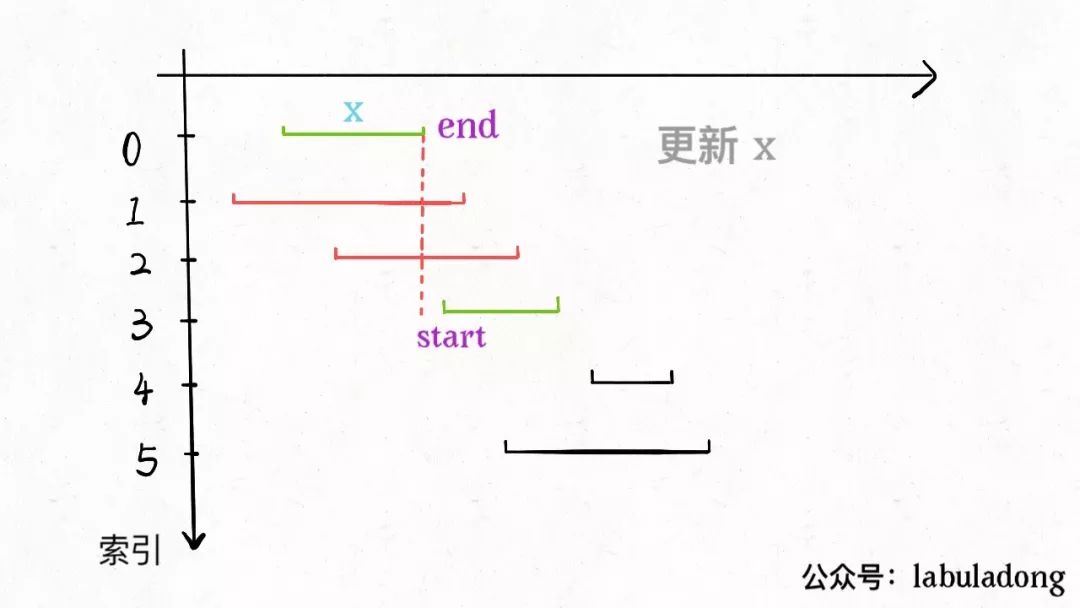
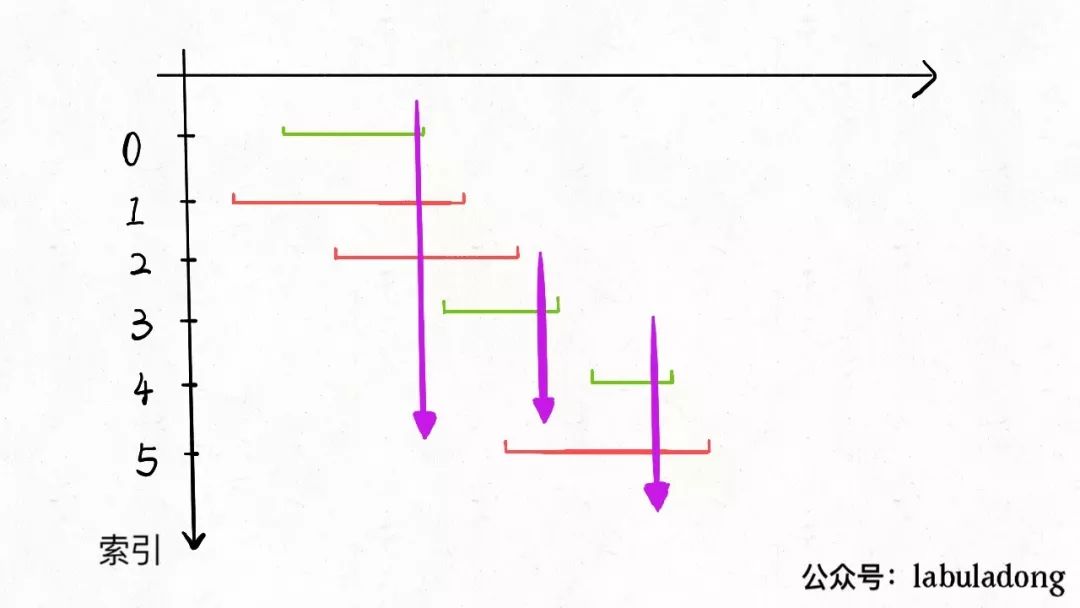
从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(end 最小)。 -
把所有与 x 区间相交的区间从区间集合 intvs 中删除。 -
重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。

三、应用举例

int eraseOverlapIntervals(int[][] intervals) {int n = intervals.length;return n - intervalSchedule(intervals);}

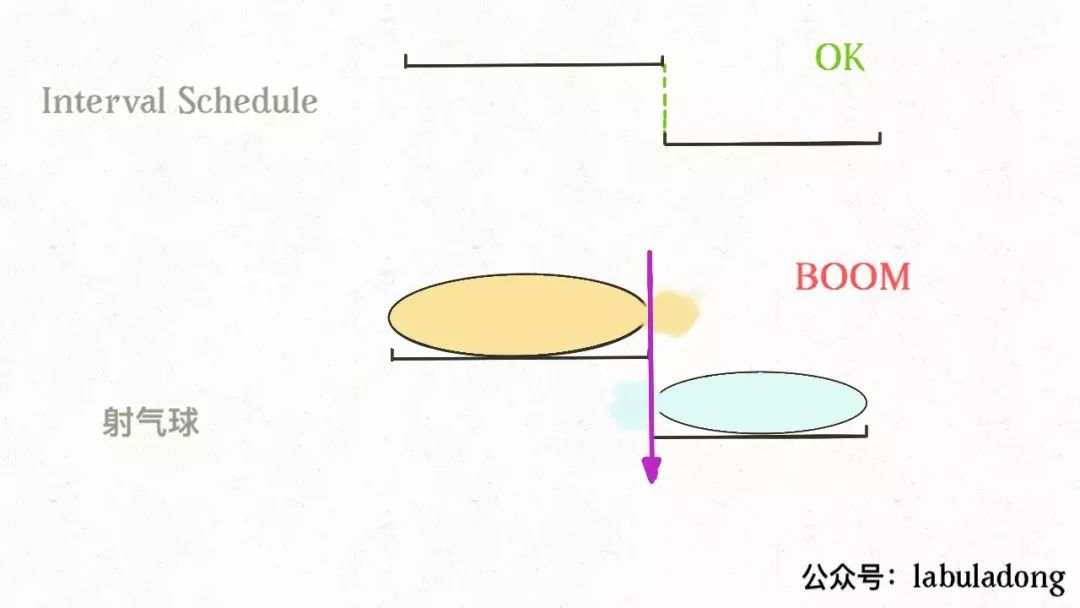
int findMinArrowShots(int[][] intvs) {// ...for (int[] interval : intvs) {int start = interval[0];// 把 >= 改成 > 就行了if (start > x_end) {count++;x_end = interval[1];}}return count;}
(*本文为 AI科技大本营转载文章,转载请联系作者)
◆
福利时刻
◆
入群参与每周抽奖~
扫码添加小助手,回复:大会,加入福利群,参与抽奖送礼!

大会5折优惠票倒计时 1 天! 团购还享立减优惠,倒计时 1 天!此外,伯克利大学名师精髓课程移师北京。《动手学深度学习》作者、亚马逊首席科学家李沐线下亲授「深度学习实训营」,免费GPU资源,现场还将限量赠送价值85元的配套书籍一本,先到先得。原价1099元,限时专享CSDN 独家福利价199元!识别海报二维码,即刻购票~
推荐阅读
:
以上是关于一份贪心算法区间调度问题解法攻略,拿走不谢的主要内容,如果未能解决你的问题,请参考以下文章
拿走不谢!一份 Tomcat 和 JVM 的性能调优经验总结!
贪心算法第五篇: 区间问题(右边界总是大于左边界-隐含条件)