常见算法——贪心算法&分治算法

Posted 2021-04-25 水之Coding工房

点击上方“水之Coding工房”并关注，更多好玩的等着你~

武汉 加油， 中国 加油！

★

大家好，我是本公众号唯一御用小编~

我叫水水。

本篇推送是

寒假学习专题的

第九篇

而本次的主题是

贪心算法 & 分治算法

我们继续学习吧~

★

简单地讲解完排序和查找算法以后，我们继续来讲解一下几种也比较基本的算法，或者也可以说是一种 算法思想 。在这些算法思想的讲解中，首先会大体讲解思想的核心，并辅之以 例子 加深记忆。而本次推送，我们先来讲一下贪心算法和分治算法。

P.S.以下讲解的算法不仅适用于编码，在生活体验和逻辑思考中也是有可取可用之处的，大家不妨学习一下哦~

贪心算法

Greedy Algorithm

贪心算法有很多经典的应用，比如霍夫曼编码、Prim和Kruskal最小生成树算法、还有Dijkstra 单源最短路径算法。那么问题来了，贪心算法到底是什么？我们该如何理解它呢？

关于贪心算法，我们可以看看一个著名的问题——“背包”问题。

假设有一个可以容纳10kg物品的背包，可以装各种物品。我们有以下5样物品（如下表），每样物品的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，我们如何选择在背包中装哪些物品？每样物品又该装多少呢？

实际上，这个问题不难，思考一下我们就知道，我们可以先计算每种物品的 单价 ，然后按照单价 由高到低 依次来装就好了。 单价从高到低排列，依次是： 口罩、酒精、方便面、自热米饭、手套，所以，我们可以往背包里装 2kg 口罩、8kg 酒精。

这个问题的解决思路显而易见，它本质上借助的就是贪心算法。 结合这个例子，我们再来看看贪心算法解决问题的步骤是怎么样的。

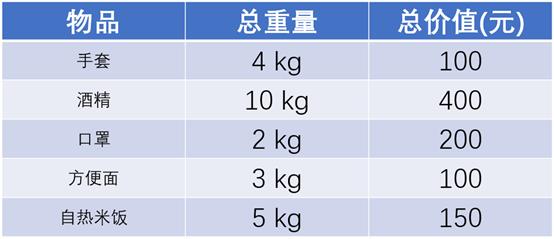
第一步，当遇到这类问题的时候，首先要联想到贪心算法：

针对一组数据，我们定义了 限制值 和 期望值 ，希望从中选出几个数据， 在满足限制值的情况下，期望值最大。 类比到刚刚的例子，限制值就是重量不能超过10kg，期望值就是物品的总价值。这组数据就是5样物品。我们从中选出一部分，满足重量不超过10kg，并且总价值最大。

第二步，尝试看下这个问题是否可以用贪心算法解决：

每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。类比到刚刚的例子，我们每次都从剩余的物品里面，选择单价最高的，也就是重量相同的情况下，对贡献值(价值)最大的物品。

 

第三步，举几个例子看下贪心算法产生的结果是否是最优的。

大部分情况下，举几个例子验证一下就可以了。 严格地证明贪心算法的正确性，是非常复杂的，需要涉及比较多的数学推理。 而且，从实践的角度来说，大部分能用贪心算法解决的问题，贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明。

但是实际上泼冷水地说明一句，用贪心算法解决问题的思路，并不总是能给出最优解。

就好比我们在数据结构的图专题中所认识到的有权图一样（如下图），我们从顶点1出发，找到一条通往顶点9的最短路径（路径中边的权值和最小）。 贪心算法的解决思路是，每次都选择一条跟当前顶点相连的权最小的边，直到找到顶点9。 按照这种思路，我们求出的最短路径是 1->3->5->8->9，路径长度是4+1+7+4=16。

但是，这种贪心的选择方式，最终求的路径并不是最短路径，因为路径1->4->6->8->9才是最短路径，因为这条路径的长度是5+2+4+4=15。 为什么贪心算法在这个问题上不工作了呢？

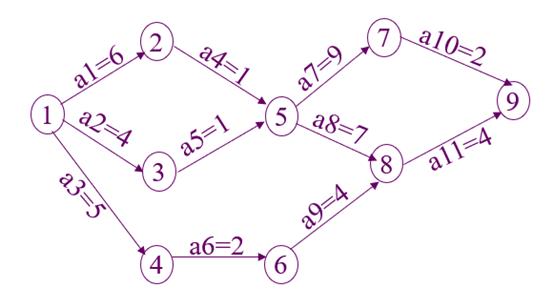
在这个问题上，贪心算法不工作的主要原因是，前面的选择，会影响后面的选择。如果我们第一步从顶点1走到顶点3，那接下来面对的顶点和边，跟第一步从顶点1走到顶点4，是完全不同的。所以，即便我们第一步选择最优的走法（边最短），但有可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也就无缘全局最优解了。

P.S.这从侧面也反映了一个人生道理(胡说八道)：可能日复一日地精打细算，确实能够让自己觉得人生中的每一步都是不会吃亏且有意义的。但是在生活之中，也可能有些时候你所做的你认为正确选择会让自己收益不多甚至吃亏，但是谁又能保证你最后所得到的收益一定就比别人少呢？那所以又何必去为一些小事或者眼前的收益而斤斤计较呢？

贪心算法实践分析

对于贪心算法的理解，我们再通过一两个具体的栗子来加深记忆。

> > > >

分糖果

我们有m个糖果和n个孩子。现在要把糖果分给这些孩子吃，但是糖果少，孩子多（m<n），所以糖果只能分配给一部分孩子。

每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小大于等于孩子的对糖果大小的需求的时候，孩子才得到满足。假设这n个孩子对糖果大小的需求分别是 g1，g2，g3，……，gn。

那么问题来了，如何分配糖果，能尽可能满足最多数量的孩子？

我们可以把这个问题抽象成，从 n 个孩子中，抽取一部分孩子分配糖果，让满足的孩子的个数（期望值）是最大的。这个问题的限制值就是糖果个数m。

现在来看看如何用贪心算法来解决。对于一个孩子来说，如果小的糖果可以满足，我们就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面，对糖果大小需求小的孩子更容易被满足，所以，我们可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子，对我们期望值的贡献是一样的。

我们每次从剩下的孩子中，找出对糖果大小需求最小的，然后发给他剩下的糖果中能满足他的最小的糖果，这样得到的分配方案，也就是满足的孩子个数最多的方案。

> > > >

钱找零

假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币，它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付A元，最少要用多少张纸币呢？

在生活中，我们肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。在贡献相同期望值（纸币数目）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。直觉告诉我们，这种处理方法就是最好的。而如果要在理论上去证明的话，所运用的知识太高深我们就不长篇大论了。

 

分治算法

Divide and Conquer

分治算法的核心思想其实就是四个字，分而治之，也就是将原问题划分成n个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

这个定义看起来有点类似递归的定义。 但在之前的排序算法中也有提及过： 分治算法是一种处理问题的思想，递归是一种编程技巧。 实际上，分治算法一般都比较适合用 递 归 来实现。 分治算法的递归实现中，每一层递归都会涉及这样三个操作：

1、分解： 将原问题分解成一系列子问题；

2、解决： 递归地求解各个子问题，若子问题足够小，则直接求解；

3、合并： 将子问题的结果合并成原问题。

分治算法能解决的问题，一般需要满足下面这几个条件：

1、 原问题与分解成的小问题具有 相同 的模式；

2、 原问题分解成的子问题可以 独立 求解，子问题之间 没有相关性 ；

3、 具有分解终止条件 ，也就是说，当问题足够小时，可以直接求解；

4、 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

分治算法应用举例

分治算法思想的应用是非常广泛的，并不仅限于指导编程和算法设计。它还经常用在大数据处理的场景中。所谓数据结构和算法，大部分都是基于内存存储处理。但是，如果要处理的数据量非常大，没法一次性放到内存中，这个时候，这些数据结构和算法就无法工作了。

比如，给10GB的订单文件按照金额排序这样一个需求，看似是一个简单的排序问题，但是因为数据量大，有10GB，而我们的机器的内存可能只有2、3GB这样子，无法一次性加载到内存，也就无法通过单纯地使用快排、归并等基础算法来解决了。

要解决这种数据量大到内存装不下的问题，我们就可以利用分治的思想。我们可以将海量的数据集合根据某种方法，划分为几个小的数据集合，每个小的数据集合单独加载到内存来解决，然后再将小数据集合合并成大数据集合。实际上，利用这种分治的处理思路，不仅仅能克服内存的限制，还能利用多线程或者多机处理，加快处理的速度。

比如刚刚举的那个例子，给10GB的订单排序，我们就可以先扫描一遍订单，根据订单的金额，将10GB的文件划分为几个金额区间。比如订单金额为1到100元的放到一个小文件，101到200之间的放到另一个文件，以此类推。这样每个小文件都可以单独加载到内存排序，最后将这些有序的小文件合并，就是最终有序的10GB订单数据了。这就是分治思想的一大体现。

■ Over ■

★

本次贪心算法&分治算法专题

就完整结束啦

我是水水

我们下期再见

下期的主题将是

动态规划

祝学习愉快鸭~

★

历史

史

文

章

有什么问题的话欢迎在后台输入框中回复哦~

武汉 加油， 中国 加油！