信息学：C++最优化问题（贪心算法）

Posted 2021-04-25 合肥编程思维

贪心算法又称贪婪算法

一、最优化问题

本文及后面介绍的算法例子都是“最优化问题”。每个最优化问题都包含一组“限制条件”和一个“优化函数”。符合限制条件的问题求解方案称为“可行解”。使优化函数可能取得最佳值的可行解称为“最优解”

二、贪婪算法思想

在贪婪算法中，我们要逐步构造一个最优解。每一步，我们都在一定的标准下，作出一个最优决策。在每一步做出的决策，在以后的步骤中都不可更改。做出决策所依据的标准称为贪婪准则

三、实际应用之找零钱

问题描述

• 顾客用美元来购买糖果，售货员希望用数目最少的硬币找给小孩零钱。假设有面值为25美分、10美分、5美分以及1美分的硬币，而且数目不限

• 售货员每次选择一枚硬币，凑成要找的零钱。选择时所依据的是贪婪准则：在不超过要找的零钱总数的条件下，每一次都选择面试尽可能最大的硬币，直到凑成的零钱总数等于要找的零钱总数

• 问题描述：假设要找给顾客67美分

贪婪算法解决步骤

假设要找给顾客67美分：

• 前两步选择的是两个25美元的硬币（第三步就不能选择25美元了，否则总数就超过67美分了）

• 第三步选择10美分的硬币

• 第四步选择5美分的硬币

• 最后一步是两个1美分的硬币

  
  

贪婪算法使我们有一种感觉：这样凑出来的零钱，硬币数目最少或接近最少

四、实际应用之最短路径

问题描述

• 一个有向网如下图所示，图中的数字代表两个节点之间的距离

• 现在有这样一个需求：从某一个点开始达到另外一个点，每一步都向路径上加入一个订单。假设当前的路径已经达到顶点q，但还未达到终点。要求下一次选择路径时：选择一个关联于q最近，且目前不在路径中的顶点

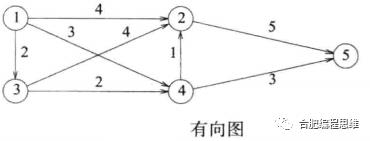
贪婪算法解决步骤

假设从顶点1达到顶点5，贪婪算法的解决办法为：

• 第一步选择1->3的路径，长度为2

• 第二步选择3->2的路径，长度为2

• 第三步选择4->2的路径，长度为1

• 第四步选择2->5的路径，长度为5

  
  

因此总共的长度为10

备注（重点）：根据问题描述与贪婪算法，最终选择出的路径为10，但是不是最短路径（不是最优的）。例如可以执行1->4->5这条路径，长度总共为6。因此贪婪算法不一定是最优解

五、一些其他属于概念

通过上面一些问题可以知道，贪婪法则虽然不能保证最优解（例如上面的最短路径问题），但是一般情况下它的解总是接近最优的。这是一种经验法则。所得的结果通常都接近最优解，这种算法称为“启发式方法”

如果启发式方法与最佳犯法之间还有一种限定关系，那么我们我们称这种启发式方法具有“限定性能”

具有限定限定性能的启发式方法称为“近似算法”

添加涵爸微信，共同交流

~关于涵爸的介绍

标签一：奶爸（这是我最自豪的，没有之一）

8年奶爸生涯刚结束

新一轮奶爸生涯又开始

小二宝悄悄降临

笑声不断，欢乐无穷

标签二：编程高手（这是我给自己封的，有待认可）

才疏学浅，短见薄识

软件开发只有10多年的经验

掌握的C++和Java技能还不够出神入化

前端html、CSS、JS的娴熟度也不足百分

大数据、云计算、人工智能等也只略知一二

虚心万事能成，自满十事九空

涵爸愿虚心学习

不辜负此“高手”二字

标签三：老师（这是自己未来的定位，还需努力）

孩子的教育大于一切

于是我放弃了高薪

编程的普及大势所趋

于是我趟了这趟浑水

能力一般，水平有限

涵爸定当全力以赴

为大家分享最优质的信息

做出最专业的课堂

关注涵爸了解更多少儿编程知识。