贪心算法千字总结

Posted 2021-04-25 昊天码字

YOU CAN DRINK ALL YOU LIKE, BUT IN THE MORNING YOU GET HEADACHE WITH THE SAME PROBLEMS.

---

0x07贪心

基础知识

贪心是一种在每次决策时采取当前意义下最优策略的算法，因此，使用贪心法要求问题的整体最优性可以由局部最优性导出。贪心算法的正确性需要证明，常见的证明手段有：

1. 微扰（邻项交换）
   证明在任意局面下，任何对局部最优策略的微小改变都会造成整体结果的变差，经常用于以“排序”为贪心策略的证明
2. 范围缩放
   证明任何对局部最优策略作用范围的扩展都不会造成整体结果的变差
3. 决策包容性
   证明在任意局面下，做出局部最优策略以后，在问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。换言之，这个局部最优策略的可能性包含其他所有策略提供的可能性
4. 反证法
5. 数学归纳法

常见套路

贪心算法是一个很难讲的东西，因为讲贪心讲的都是怎样去证明这种做法是对的，而证明算法是对的在做题的过程中用处不大，因为如果你的思路能AC的话，没必要浪费时间去证明正确性，只有给别人讲题的时候证明算法是对的才有必要

那么贪心的套路是什么？一个字“蒙”，如果给一个序列的数字，那就先把序列升序或降序排列；如果给一个序列的范围，那么就把范围的起始点或中止点升序或降序排列，然后用笔在纸上模拟程序运行过程，如果哪一种思路符合样例，那么这种贪心的思路就是正确的，没必要证明（大佬除外）

我们通过几道例题来介绍贪心算法的应用

ACWING110.防晒

题目描述在文章末尾的原文链接中

按照minSPF递减的顺序把奶牛排序，依次考虑每头奶牛

对于每头奶牛，扫描一遍所有的防晒霜，在这头奶牛能用（能用指的是该防晒霜的强度符合这头奶牛的范围，并且瓶数还有剩余）的防晒霜里找SPF值最大的使用

以上算法的贪心策略是在满足条件的前提下每次选择SPF最大的防晒霜，这个策略正确的原因是：我们考虑这一步策略的作用范围扩展到后续其他奶牛之后产生的影响。每瓶防晒霜是否可用，会被minSPF和maxSPF两个条件限制，因为奶牛已经按照minSPF递减排序，所以每一个不低于当前奶牛minSPF值的防晒霜，都不会低于后面其他奶牛的minSPF。也就是说，对于当前奶牛可用的任意两瓶防晒霜x和y，如果SFP[X]<SFP[y]，那么后面的奶牛只可能出现三种情况之一

1. x和y都能用
   

2. x和y都不能用

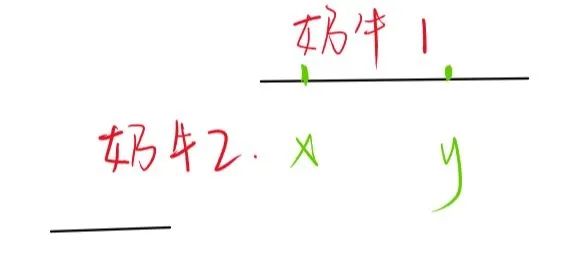
3. x能用，y不能用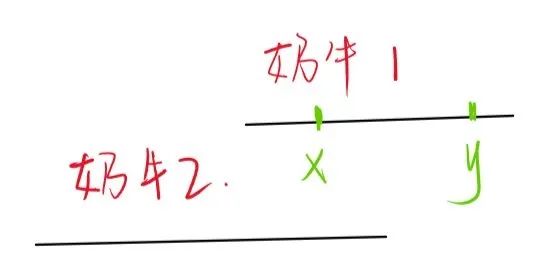
   

因此当前奶牛选择较大的y去用，对于整体的影响肯定比选择较小的x去用要好，另外，每头奶牛对答案的贡献至多是1，即使让当前奶牛放弃日光浴，留下防晒霜给后面的某一头奶牛去用，对答案的贡献也不会更大，综上所述，尽量满足当前的奶牛，并选择SPF值尽量大的防晒霜是一个正确的贪心策略

#include <bits/stdc++.h>
using namespace std;

const int N = 2510;
typedef pair<int, int> PII;
int n, m;
PII cows[N];

int main() {
    cin >> n >> m;
    map<int, int> spfs;
    for (int i = 0; i < n; i++) cin >> cows[i].first >> cows[i].second;
    for (int i = 0; i < m; i++) {
        int spf, cover;
        cin >> spf >> cover;
        spfs[spf] += cover;
    }
    sort(cows, cows + n);
    int res = 0;
    spfs[0] = spfs[1001] = 1;
    for (int i = n - 1; i >= 0; i--) {
        auto spf = spfs.upper_bound(cows[i].second);
        spf--;
        if (spf->first >= cows[i].first) {
            res++;
            if (--spf->second == 0)
                spfs.erase(spf);
        }
    }
    cout << res << endl;
    return 0;
}

ACWING111.畜栏预定

题目描述在文章末尾的原文链接中，在右上角的题库中搜111即可

按照开始吃草的时间把牛排序，用小根堆维护所有畜栏中最后一头牛结束吃草的时间的最小值，每循环到一头牛，如果这头牛的吃草开始时间比这个小根堆的堆顶大，则把这个牛插入到这个小根堆堆顶对应的畜栏中，再重新维护小根堆；如果小根堆的堆顶比这头牛的开始吃草时间大，则新建一个畜栏，插入到小根堆中

这种策略成功的原因在于：把每个畜栏的时间都充分利用，如果存在多个畜栏可以存放此牛，则选择最后一头牛结束吃草时间最小的畜栏，这样可以充分利用每个畜栏的时间；把每个牛的开始吃草时间从小到大排序的原因是，这样就可以让后面的牛插入在畜栏的后面，如果不排序，则每个畜栏前面可能有时间空隙放牛，这是不符合要求的，很难做出来

#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
const int N = 50010;

int n;
int id[N];
pair<PII, int> cows[N];

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> cows[i].first.first >> cows[i].first.second;
        cows[i].second = i;
    }
    sort(cows, cows + n);

    priority_queue<PII, vector<PII>, greater<PII> > heap;
    for (int i = 0; i < n; i++) {
        if (heap.empty() || heap.top().first >= cows[i].first.first) {
            id[cows[i].second] = heap.size() + 1;
            heap.push({cows[i].first.second, heap.size() + 1});
        } else {
            auto stall = heap.top();
            heap.pop();
            stall.first = cows[i].first.second;
            id[cows[i].second] = stall.second;
            heap.push(stall);
        }
    }

    cout << heap.size() << endl;
    for (int i = 0; i < n; i++) cout << id[i] << endl;
    return 0;
}